SHAPIRO’S CATALAN CONVOLUTION
G´abor V. Nagy
Bolyai Institute, University of Szeged, Szeged, H-6720, Hungary
Abstract. Shapiro proved an elegant convolution formula involving Catalan num- bers of even index. This paper gives a combinatorial proof of his formula. In addition, we show that it is equivalent to an alternating convolution formula of central binomial coefficients.
1. Introduction
In this paperCndenotes thenth Catalan number andBndenotes thenth central binomial coefficient, i.e.Cn= n+11 2nn
andBn= 2nn
. Unless otherwise stated, all indices (i,j,k, and so on) are nonnegative integers in our formulas.
In 2002, L. Shapiro found the following elegant identity [3; p. 123]:
Theorem 1.
X
i+j=n
C2iC2j= 4nCn. (1)
This can be easily proved using generating functions, but according to Stanley [5; p. 46], no simple direct combinatorial proof has been known (see [1] for another combinatorial proof). In Section 3 we will give a simple combinatorial proof of the the following equivalent version of Theorem 1:
Theorem 2.
X
i+j=n
C2iB2j= 4nBn. (2)
(1) and (2) are equivalent, because
X
i+j=n
C2iB2j =1 2
X
i+j=n
C2i(2j+ 1)C2j+ X
i+j=n
(2i+ 1)C2iC2j
=1 2
X
i+j=n
(2n+ 2)C2iC2j= (n+ 1) X
i+j=n
C2iC2j.
1991Mathematics Subject Classification. 05A10; 05A19.
Key words and phrases. Catalan numbers; Shapiro convolution.
Supported by the T ´AMOP-4.2.1/B-09/1/KONV-2010-0005 project.
The publication is supported by the European Union and co-funded by the European Social Fund. Project title: “Broadening the knowledge base and supporting the long term professional sustainability of the Research University Centre of Excellence at the University of Szeged by ensuring the rising generation of excellent scientists.” Project number: T ´AMOP-4.2.2/B-10/1- 2010-0012
The key observation of this paper is a non-standard interpretation ofC2n, that is discussed in the next section. Using that, we can give a new combinatorial meaning of the left-hand sides of (1) and (2). In Section 4, we show bijectively that (2) is equivalent with the alternating convolution formula of central binomial coefficients, which has a nice combinatorial interpretation, due to Spivey [4].
2. Even-zeroed balanced paths and C2n
Apath of lengthlis anl-element sequence of up-steps (%) and down-steps (&).
A balanced n-path is such a path of length 2n that has n up-steps and n down- steps. The number of balancedn-paths is clearlyBn. We denote byBn the set of balancedn-paths. We visualize paths in the usual way: They start from the origin,
%is a step (1,1) and& is a step (1,−1); see the figures below. An n-Dyck-path (of length 2n) is a balancedn-path such that it never falls below thex-axis. It is well-known that the number of n-Dyck-paths is Cn. We denote by Cn the set of n-Dyck-paths. A signedn-Dyck-path is an element of the set Sn :={+,−} × Cn. The set of signed Dyck-paths is denoted byS:=S∞
i=0Si. The number of up-steps (or down-steps) in a signed or unsigned balanced path P is called the parameter of P and it is denoted by par(P). A special type of path plays a crucial role in our proofs, so we introduce a new terminology for them: We call a (balanced or non-balanced) patheven-zeroed, if itsx-intercepts are all divisible by 4.
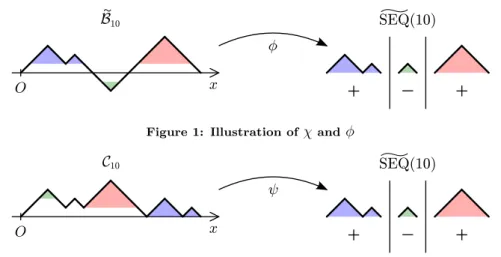
Ifn≥1, then every balancedn-path can be decomposed uniquely into a sequence of signed Dyck-paths in a very natural way (see Figure 1): The x-axis cuts the balanced path into nonempty subpaths so that every subpath is either a Dyck-path that never touches the x-axis (apart from its starting point and end point), or the reflection of such a Dyck-path across the x-axis. Every subpath is uniquely characterized by a signed Dyck-path that we get after removing the first and last steps (+: standard Dyck-path,−: reflected Dyck-path), and we can list these signed Dyck-paths (from left to right) in a sequence. It is very easy to see that we defined a bijectionχ betweenBn and SEQ(n), where
SEQ(n) = (
(P1, . . . , Pk) :k∈Z+, Pi∈ S for alli, and
k
X
i=1
(par(Pi) + 1) =n )
.
Now we are ready to prove the key lemma of this paper:
Lemma 3. C2n counts the number of even-zeroed balanced2n-paths.
Proof. The statement is true forn= 0. Now let us assume thatn≥1.
Clearly, a balanced 2n-pathP is even-zeroed, if and only if all the signed Dyck- paths in its sequence χ(P) have odd parameter. So if we denote by ˜B2n the set of even-zeroed 2n-paths, the restriction ofχ to ˜B2n gives a bijectionφ between ˜B2n
andSEQ(2n), where]
SEQ(2n) =] (
(P1, . . . , Pk) :Pi∈ S, par(Pi) is odd∀i;
k
X
i=1
(par(Pi) + 1) = 2n )
.
Now we define a bijectionψbetweenC2nand]SEQ(2n) and so we give a bijective proof of the lemma (φ−1◦ψ is a bijection between C2n and ˜B2n). Consider an
arbitrary 2n-Dyck-path D. It is well-known from a standard proof of the Catalan recursion that D can be uniquely written as %L&R, i.e. D can be decomposed into an ordered pair (L, R), whereLandRare Dyck-paths, whose parameters sum to 2n−1. Either par(L) or par(R) is odd. If par(L) is odd, then we define the first element ofψ(D) to be−L, and we recursively repeat the process forD0 :=R (par(R) is even) to get the other elements of ψ(D). If par(R) is odd, then we define the first element of the ψ(D) to be +R, and recursively repeat the process for D0 := L. (− means “left”, + means “right” here.) The process terminates whenD0 is the empty 0-Dyck-path. It is easy to check that the obtainedψ(D) is inSEQ(2n). See Figure 2 for a visualization.]
One can easily compute ψ−1(S) for an arbitrary S ∈ SEQ(2n), so we indeed] defined a bijection.
O
x
B
10SEQ(10)
Figure 1: Illustration ofχand φ
O
x
C
10
SEQ(10)
Figure 2: Illustration ofψ
Remarks. Roughly speaking, our bijectionC2n→B˜2n converts the “left-right sym- metry” ofC2n into the “up-down symmetry” of ˜B2n.
When definingψ, it might be slightly more natural to work with full binary trees that is an other representation of Catalan numbers (what we do here is to decompose even-parameter full binary trees into odd-parameter subtrees – the details are left to reader). But then φ−1◦ψ would become slightly less intuitive, since we would need an extra conversion between full binary trees and Dyck-paths.
If we already know or conjecture that |B˜2n|=C2n, we can find a quicker (but recursive) argument for this. Namely, using the notations Xn :=|B˜2n| andYn :=
C2n, one can quickly figure out that both (Xn)∞n=0and (Yn)∞n=0satisfy the following recursion: Z0= 1, Zn= 2Pn
k=1C2k−1Zn−k (ifn≥1).
As an application, we prove a lemma, from which a recursive proof of Theorem 2 can be obtained.
Lemma 4.
2· X
i+j+k=n
C2iC2jB2k=B2n+1.
Proof. Both sides count the number of balanced (2n+ 1)-paths. This is obvious for the right-hand side. In the left-hand side, we group the balanced (2n+ 1)-paths
by the position (i) and length (j) of the leftmost such signed Dyck-path segment (cut by thex-axis) whose parameter is odd. Such a segment must exist, since the sum of the parameters is 2n+ 1. If the starting point of that segment is 4iand its parameter is 2j+ 1, then by Lemma 3, there areC2i even-zeroed balanced paths from the origin to 4i, there are 2C2j possible choices for the segment in question, and there areB2k possible endings for the rest of the path (k=n−i−j).
Remark. Using the well-known [2] convolution identity P
i+j=nBiBj = 4n and Lemma 4, it is easy to see that that both sides of (2) satisfy the following recursion:
X0= 1, P
s+t=nXsXt= 16n. This is because
X
s+t=n
4sBs·4tBt= 4n· X
s+t=n
BsBt= 4n·4n= 16n,
and
X
s+t=n
X
i+k=s
C2iB2k
! X
j+l=t
C2jB2l
!
= X
i+j+k+l=n
C2iC2jB2kB2l
= X
m+l=n
X
i+j+k=m
C2iC2jB2k
! B2l=1
2 · X
m+l=n
B2m+1B2l
=1 2 ·1
2 ·42n+1= 16n.
3. The proof of Theorem 2
The following lemma is well-known, and it has several combinatorial proofs [2].
Lemma 5. Bn counts the number of paths of length 2n that never return to the x-axis after the first step.
With the help of Lemma 3, we can give an interesting combinatorial interpreta- tion of the left-hand sides of (1) and (2).
Lemma 6. a)P
i+j=nC2iB2j is the number of even-zeroed paths of length 4n.
b)P
i+j=nC2iC2j is the number of even-zeroed paths from the origin to(4n+ 1,1).
Proof. a) By Lemmas 3 and 5, there are C2iB2(n−i) such even-zeroed paths of length 4nwhose rightmostx-intercept is 4i.
b) There areC2iC2(n−i)such even-zeroed paths from the origin to (4n+ 1,1) whose rightmost x-intercept is 4i (followed by an up-step). The first factor comes from Lemma 3 and the second one comes from the standard interpretion ofC2(n−i) by Dyck-paths.
1 1
1 1
1 1
1 1
1
1 1
1 1
1 1
1 1 1
1 2 2 2
3 4 4 3
4 7
7 4
5 11
7 7 11
5 6 16 18 14 18 16 6
x
Figure 3: The number of even-zeroed paths
In Figure 3 the label of a node shows the number of even-zeroed paths from the origin to that node. These labels can be calculated recursively, since every label is the sum of its left neighbors. We already know that the label of (4n,0) isC2n, the label of (4n+ 1,±1) isLn :=P
i+j=nC2iC2j and the sums of the labels in the 4nth column isSn:=P
i+j=nC2iB2j. In order to prove Theorem 2, we only have to show thatSn= 4nBn. The key observation is thatSn+1can be calculated from Sn andLn easily, but we know from Section 1 that Ln = n+11 Sn, so in fact Sn+1
can be calculated fromSn easily. This calculation is done in the next lemma, which implies Theorem 2.
Lemma 7. The number of even-zeroed paths of length4nis4nBn.
Proof. LetPndenote the set of even-zeroed paths of length 4n, and setSn:=|Pn|.
By induction onn, we prove thatSn= 4nBn. This is obviously true ifn= 0.
Let us assume thatSn= 4nBnholds. Clearly, every path ofPn+1is an extension of a path of Pn by 4 steps. For each path ofPn there are 16 possible extensions.
But some of the 16Sn extensions are not inPn+1. These “wrong” extenstions are exactly the even-zeroed paths from the origin to (4n+ 1,1) followed by a down-step and two arbitrary steps, and the reflections of these paths across the x-axis. By Lemma 6.b, the number of these wrong extensions is 8P
i+j=nC2iC2j, that equals to n+18 P
i+j=nC2iB2j = n+18 Sn, as seen in Section 1 and Lemma 6.a. By the induction hypothesis, Sn = 4nBn, thus Sn+1 = 16·4nBn −n+18 4nBn. A quick calculation shows thatSn+1= 4n+1Bn+1.
4. Alternating convolution of the central binomial coefficients
The following theorem has a nice combinatorial proof using random colored permutations, due to Spivey [4]:
Theorem 8.
X
i+j=n
B2iB2j− X
i+j=n j≥1
B2i+1B2j−1= 4nBn.
By proving the next theorem bijectively, we will see that Theorem 8 is equivalent with Theorem 2, so any combinatorial proof of Theorem 8 yields a combinatorial proof of Theroem 2. Conversely, our proof in the previous section can be interpreted as a new proof of Theorem 8.
Theorem 9.
X
i+j=n
B2iB2j− X
i+j=n j≥1
B2i+1B2j−1= X
i+j=n
C2iB2j.
Proof. Using Lemma 3, we will prove the following equivalent form:
X
i+j=n
(B2i−C2i)B2j= X
i+j=n j≥1
B2i+1B2j−1. (3)
The right-hand side counts the number of pairs (O1, O2), where O1and O2 are balanced paths with odd parameters, and par(O1)+par(O2) = 2n. LetObe the set of these pairs. By Lemma 3, the left-hand side counts the number of pairs (E1, E2), whereE1 andE2 are balanced paths with even parameters,E1 has anx-intercept of the form 4t+ 2 (for some integert), and par(E1) + par(E2) = 2n. LetE be the set of these pairs.
We will give a bijection betweenEandO, which means that|E|=|O|, as stated.
Pick an arbitrary element (E1, E2) of E. Let L be the subpath of E1 which is identical withE1from the origin to its leftmostx-intercept of the form 4t+ 2, and letR be the rest ofE1. Then the image of (E1, E2) is defined as (LE2, R), where LE2 is the concatenation of L and E2 in this order. It is easy to see that this mapping is bijective.
E
1E
2O
1O
2L R L E R
2
Figure 4: Illustration of the proof of Theorem 9
If we writeC2i= 4i2i
− 2i−14i
in (3), we get the following identity:
Corollary 10.
n
X
i=1
4i 2i−1
4n−4i 2n−2i
=
n−1
X
i=0
4i+ 2 2i+ 1
4n−4i−2 2n−2i−1
.
References
[1] G. E. Andrews, On Shapiro’s Catalan convolution, Adv. in Appl. Math. 46 (2011) 15–24.
[2] ¨O. E˘gecio˘glu, A. King, Random walks and Catalan factorization, Congr. Numer. 138 (1999) 129–140.
[3] T. Koshy, Catalan Numbers with Applications, Oxford University Press, New York, 2009.
[4] M. Spivey, Combinatorial interpretation of the alternating convolution of the central binomial coefficients, http://mikespivey.wordpress.com/2012/03/16/altconvcentralbinom/, 2012.
[5] R. P. Stanley, Bijective proof problems, http://www-math.mit.edu/˜rstan/bij.pdf, 2009.