Matematika
Matematika
Kocsis Imre
TERC Kft. • Budapest, 2013
© Kocsis Imre, 2013
Kézirat lezárva: 2012.
ISBN 978-963-9968-69-1
Kiadja a TERC Kereskedelmi és Szolgáltató Kft. Szakkönyvkiadó Üzletága, az 1795-ben alapított Magyar Könyvkiadók és Könyvterjesztők Egyesülésének a tagja
A kiadásért felel: a kft. igazgatója Felelős szerkesztő: Lévai-Kanyó Judit
Műszaki szerkesztő: TERC Kft.
Terjedelem: 6 szerzői ív
TARTALOMJEGYZÉK
ELŐSZÓ ... 9
1. LOGIKAI FÜGGVÉNYEK ... 10
1.1 A LOGIKAI FÜGGVÉNYEK SZEREPE ... 10
1.2 A LOGIKAI FÜGGVÉNYEK MEGADÁSA ... 10
1.3 NORMÁLFORMÁK ... 12
1.4 A LOGIKAI FÜGGVÉNYEK EGYSZERŰSÍTÉSE ... 13
2. KOMPLEX SZÁMOK ... 18
2.1 A KOMPLEX SZÁMOK KÜLÖNFÉLE ALAKJAI, ELNEVEZÉSEK ... 18
2.2 ALAPMŰVELETEK, HATVÁNYOZÁS, GYÖKVONÁS ... 19
2.3 SZÁMOLÁS VÁLTAKOZÓÁRAMÚ HÁLÓZATOKBAN ... 20
3. DIFFERENCIÁLÁS ... 27
3.1 LINEÁRIS FÜGGVÉNYEK ... 27
3.2DIFFERENCIÁLHÁNYADOS; DERIVÁLT FÜGGVÉNY ... 28
3.3 VÁLTOZÁSI GYORSASÁG ... 31
3.4 IRÁNY MENTI DERIVÁLT; PARCIÁLIS DERIVÁLT ... 34
3.5 A TÉRGÖRBÉK GÖRBÜLETE ÉS TORZIÓJA ... 36
3.6 VEKTORMEZŐK DIVERGENCIÁJA ÉS ROTÁCIÓJA ... 38
3.7 PRIMITÍV FÜGGVÉNY; POTENCIÁLFÜGGVÉNY ... 41
4. INTEGRÁLÁS ... 44
4.1 INTEGRÁLRA VEZETŐ PROBLÉMÁK ... 44
4.2 JORDAN‐MÉRTÉK; HALMAZ FELOSZTÁSA ... 47
4.3 INTEGRÁLKÖZELÍTŐ ÖSSZEGEK ... 48
4.4 SKALÁRÉRTÉKŰ FÜGGVÉNYEK INTEGRÁLJA ... 52
4.4.1 Az n típusú függvények integrálja ... 52
4.4.2 Az integrál néhány alapvető tulajdonsága ... 52
4.4.3 típusú függvények integrálja ... 53
4.4.4 2 típusú függvények integrálja ... 54
4.4.5 3 típusú függvények (skalármezők) integrálja ... 54
4.4.6 Az integrál kiszámítása polár‐ és hengerkoordinátákkal ... 54
4.5 IMPROPRIUS INTEGRÁL ... 56
4.6 VEKTORÉRTÉKŰ ÉS KOMPLEX ÉRTÉKŰ FÜGGVÉNYEK INTEGRÁLÁSA ... 57
4.7 VEKTORMEZŐK INTEGRÁLÁSA ... 57
4.7.1 Erőtér munkája; görbe menti integrál ... 57
4.7.2 Felület menti integrál; fluxus ... 59
4.7.3 Kapcsolatok az integrálok között ... 60
4.8 AZ INTEGRÁL KISZÁMÍTÁSA ... 62
4.8.1 Newton–Leibniz‐formula ... 62
4.8.2 Görbe menti integrál kiszámítása potenciálos terekben ... 63
4.8.3 Numerikus integrálás (közelítőmódszerek) ... 63
5. FOURIER‐ANALÍZIS ... 66
5.1 FOURIER‐SOROK ... 66
5.1.1 Hilbert‐tér; a Fourier‐sor általános fogalma ... 66
5.1.2 Exponenciális Fourier‐sorok ... 68
5.1.3 Trigonometrikus Fourier‐sorok ... 68
5.2 INTEGRÁLTRANSZFORMÁCIÓK ... 76
5.3 FOURIER‐TRANSZFORMÁCIÓ ... 77
5.3.1 Fourier‐integrál; Fourier‐transzformált ... 77
5.3.2 A Fourier‐transzformáció néhány alapvető tulajdonsága ... 80
5.3.3 Megjegyzések a jelfeldolgozással kapcsolatban ... 81
6. LAPLACE‐TRANSZFORMÁCIÓ; LINEÁRIS RENDSZEREK ELEMZÉSE ... 82
6.1 LAPLACE‐TRANSZFORMÁCIÓ ... 82
6.1.1 A Laplace‐transzformáció fogalma ... 82
6.1.2 A Laplace‐transzformáció néhány tulajdonsága ... 84
6.2 LINEÁRIS RENDSZEREK ... 85
6.2.1 Lineáris rendszerek leírása az időtartományban ... 85
6.2.2 A homogén lineáris konstansegyütthatós differenciálegyenletek megoldáshalmaza ... 86
6.2.3 Az inhomogén lineáris konstansegyütthatós differenciálegyenletek megoldáshalmaza ... 89
6.3 VIZSGÁLÓFÜGGVÉNYEK; SÚLYFÜGGVÉNY ... 90
6.4 A LAPLACE‐TRANSZFORMÁCIÓ ALKALMAZÁSA A LINEÁRIS RENDSZEREK VIZSGÁLATÁBAN ... 92
6.5 LINEÁRIS RENDSZEREK VIZSGÁLATA A FREKVENCIATARTOMÁNYBAN ... 93
6.6 LINEÁRIS KEZDETIÉRTÉK‐PROBLÉMÁK MEGOLDÁSA LAPLACE‐TRANSZFORMÁCIÓVAL... 94
FELHASZNÁLT SZAKIRODALOM ... 97
ALKALMAZOTT JELÖLÉSEK
a természetes számok halmaza az egész számok halmaza ℚ a racionális számok halmaza
a valós számok halmaza a komplex számok halmaza [a,b] zárt intervallum ]a,b[ nyílt intervallum
Mn×k az n×k típusú valós mátrixok halmaza detA az A mátrix determinánsa
AT az A mátrix transzponáltja i képzetes egység
Re(z) a z komplex szám valós része Im(z) a z komplex szám képzetes része
z a z komplex szám konjugáltja
~u komplex feszültség
~i komplex áramerősség
v vektor
b
a skaláris szorzat b
,
a skaláris szorzat b
a vektoriális szorzat c
b
a vegyes szorzat b
a diadikus szorzat , hossz, norma
[] fizikai mértékegység (fizikai dimenzió)
nabla operátor
Laplace-operátor
x elsőrendű parciális derivált
2xy
másodrendű parciális derivált
v irány menti derivált grad gradiens div divergencia rot rotáció
görbület
torzió
mérték
fˆk Fourier-együttható FS Fourier-sor
FI Fourier-integrál FT Fourier-transzformált
FT -1 inverz Fourier-transzformált L{f} Laplace-transzformált L-1{f} inverz Laplace-transzformált f*g konvolúció
1(t) egységugrásfüggvény
(t) Dirac-delta függvény H(s) átviteli függvény w(t) súlyfüggvény v(t) átmeneti függvény
ÁBRÁK JEGYZÉKE
2.1 ábra: Komplex számsík ... 18
2.2 ábra: Komplex számok összeadása ... 19
2.3 ábra: Komplex számok szorzása ... 19
2.4. ábra: Komplex feszültség- és áramfüggvények ... 22
2.5 ábra: Ellenállás, kondenzátor, tekercs impedanciája ... 23
3.1 ábra: Kísérő triéder, síkok ... 37
4.1 ábra: Erőtér adott görbe menti munkája ... 58
4.2 ábra: Vektortér fluxusa ... 59
4.3 ábra: A Gauss–Osztrogradszkij-tétel mennyiségeinek szemléltetése ... 62
4.4 ábra: A Stokes-tétel mennyiségeinek szemléltetése ... 62
5.1 ábra: Periodikus jel frekvenciaspektruma ... 69
5.2 ábra: tcos
k0t
függvények, k ... 715.3 ábra: t sin
k0t
függvények, k ... 715.4 ábra: Konvolúció... 77
5.5 ábra: A Fourier-transzformáció és az inverz Fourier-transzformáció ... 78
5.6 ábra: A valós és a komplex spektrum összehasonlítása ... 80
6.1 ábra: A rugalmas mechanikai lengőrendszer modellje ... 87
6.2 ábra: Tranziens rezgés kis és nagy csillapítás esetén ... 88
6.3 ábra: A Dirac-delta függvény származtatása ... 91
6.4 ábra: Egységugrásfüggvény ... 92
6.5 ábra: Nykvist- és Bode-diagram ... 94
ELŐSZÓ
A Létesítménymérnöki mesterképzés „Matematika” című tárgyának oktatásakor elsődleges feladatunknak azt tekintjük, hogy rávilágítsunk a műszaki tárgyak tananyagának matematikai vonatkozásaira. Ehhez (és a terjedelmi korláthoz) alkalmazkodva e jegyzet felépítése rendhagyó, néhány témakör rövid összefoglalását tartalmazza kézikönyvszerűen. Az érintett témakörök számos matematika tankönyvben és jegyzetben megjelennek, a szándék nem ezek szaporítása volt, hanem egy olyan típusú feldolgozás, ami a műszaki tartalomnak a matematika oktatásában való megjelenésére adhat mintát.
A szemléletmódot közel állónak érezzük a [2] forráséhoz. A „Fourier-analízis”, valamint a
„Laplace-transzformáció, lineáris rendszerek” c. részeket az [1] forrás letisztult gondolatmenetére és a [3] gazdag tartalmára alapoztuk. A szöveg, jellege miatt nem tartalmaz tételes hivatkozásokat.
1. LOGIKAI FÜGGVÉNYEK
1.1 A logikai függvények szerepe
A digitális technika eszközrendszerét meghatározza az a tény, hogy az adatok kétállapotú tárolóelemekben (memóriacellákban) bináris formában vannak tárolva. Így a legbonyolultabb rendszerek állapotainak leírása és a legbonyolultabb manipulációk kódja is végeredményben bináris jelsorozat. Ha analóg eszközt akarunk kezelni digitális rendszerrel, akkor a feldolgozáshoz az analóg jelet digitálissá kell alakítani, a beavatkozáshoz pedig vissza kell alakítani analóggá. A digitális rendszerekben való problémamegoldás végső soron azt jelenti, hogy a „bemeneten” megjelenő, a vizsgált rendszer állapotát leíró (véges hosszúságú) bináris jelsorozatra a „kimeneten”, egy másik, a beavatkozást kódoló (véges hosszúságú) bináris jelsorozatot kell előállítani.
A digitális technikában használt két bináris jelet a 0 és az 1 jelöli. Ennek a számábrázolásban is haszna van, hiszen a kettes számrendszerben is ezt a két jelet használjuk. Azokat a függvényeket, amelyek véges bináris jelsorozathoz véges bináris jelsorozatot rendelnek, logikai függvényeknek nevezzük. Az elnevezés onnan ered, hogy a bináris jelek kezelésére a matematikai logika fogalmait, műveleteit használjuk (ezek eredetileg az igaz-hamis logikai értékkel való számolásra szolgáltak), függetlenül attól, hogy a bináris jelek az adott esetben logikai értéket jelentenek-e.
1.2 A logikai függvények megadása
A logikai függvények {0,1}n {0,1}k típusú függvények, ahol n és k pozitív egész számok. Egy {0,1}n {0,1}k típusú függvény előállítható k db {0,1}n {0,1} típusú függvénnyel, mint koordinátafüggvénnyel.
A továbbiakban ilyen {0,1}n {0,1} típusú (n-változós) függvényekkel foglalkozunk, amelyek egy n hosszúságú bináris jelsorozathoz egy bináris jelet rendelnek. Könnyen belátható, hogy 22nkülönböző n-változós logikai függvény létezik: a lehetséges bemenetek száma 2n, és azt, hogy ezek közül melyekhez tartozik „1” kimenet ennyi féleképpen lehet megadni (ennyi a részhalmazok száma).
Egyváltozós logikai függvények
4 féle egyváltozós logikai függvény létezik, ezek foglalja össze a táblázat:
X X
0 0 0 1 1 1 0 1 0 1
Az egyváltozós logikai függvények közül a negáció (invertálás) függvényt érdemes kiemelni, mely a bemenet értékét 0-ról 1-re, 1-ről pedig 0-ra változtatja. Ennek jelölése:
X X .
Kétváltozós logikai függvények
16 féle kétváltozós logikai függvény létezik, ezeket foglalja össze a következő táblázat.
X Y X Y (AND)
X+Y (OR)
Y X (NOR)
Y X (NAND)
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
A kétváltozós logikai függvények közül a konjunkció (ÉS, AND, szorzás), a diszjunkció (VAGY, OR, összeadás) függvényeket, valamint ezek negáltjait a NAND és a NOR függvényeket emeltük ki, mivel ezek a függvények alapvető szerepet játszanak a logikai függvényekkel való számolásokban, illetve a logikai függvények fizikai megvalósításában (a gyakorlatban elsősorban NAND, illetve NOR kapukat használnak).
A logikai függvények megadásának a fentiekben használt módját igazságtáblázatnak nevezzük. A gyakorlatban az jellemző, hogy a megoldandó probléma meghatározza a megvalósítandó logikai függvény értékeit, vagyis az igazságtáblázatát, ezután következik a formális leírás, majd az egyszerűsítés és végül a fizikai megvalósítás.
A kettőnél több változós logikai függvények esetén a fentieknek megfelelően kell az igazságtáblázatot elkészíteni.
Példa:
Jól ismert feladat a szavazógép logikai függvényének felírása. Három szavazó van (A, B, C), akik igennel (1 input) vagy nemmel (0 input) szavaznak. Az előterjesztést akkor fogadják el (1 output), ha többségben vannak az igenek, különben elvetik (0 output). A szavazógép logikai függvénye:
X Y Z f(X,Y,Z) 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1
1.3 Normálformák
Diszjunktív normálformáról beszélünk, ha a logikai függvény a változók és negáltjaik konjunkcióinak diszjunkciója. Például egy háromváltozós logikai függvény diszjunktív normál formában: f(X,Y,Z)XYZXYZXYZXYZ.
Az igazságtáblázatból könnyen felírható a diszjunktív normálforma. A fenti szavazógép esetén például:
X Y Z f(X,Y,Z)
0 0 0 0
Z Y X Z Y X Z Y X Z Y X ) Z , Y , X (
f
0 0 1 0
0 1 0 0
0 1 1 1 XYZ
1 0 0 0
1 0 1 1 XYZ 1 1 0 1 XYZ 1 1 1 1 XYZ
A diszjunktív normálformában szereplő konjunkciókat mintermeknek nevezzük. Egy minterm egyértelműen azonosítható úgy, hogy megadjuk, mely változók szerepelnek ponált, illetve negált formában. Ha ezt az 1 és a 0 jelekkel tesszük, akkor a kód bináris számként fogható fel, és decimális alakban is kifejezhető. A háromváltozós példánkban:
Z Y
X XYZ XYZ XYZ bináris kód 0 1 1 1 0 1 1 1 0 1 1 1
decimális megfelelő 3 5 6 7
a minterm jelölése m33 m35 m36 m37 A függvény jelölése: 3 37
33 6 3 5
3 m m m (3,5,6,7) m
f
Konjunktív normálformáról beszélünk, ha a logikai függvény a változók és negáltjaik diszjunkcióinak konjunkciója. Például egy háromváltozós logikai függvény konjunktív normálformában: f(X,Y,Z)(XY Z)(XYZ)(X YZ)(XY Z).
A konjunktív normálformában szereplő diszjunkciókat maxtermeknek nevezzük. Egy maxterm egyértelműen azonosítható úgy, hogy megadjuk, mely változók szerepelnek ponált, illetve negált formában. Ha ezt az 1 és a 0 jelekkel tesszük, akkor a kód bináris számként fogható fel, és decimális alakban is kifejezhető. A háromváltozós példánkban:
Z Y
X XYZ XY Z X YZ bináris kód 1 1 1 1 0 1 0 1 0 0 0 0
decimális megfelelő 7 5 2 0
a minterm jelölése M37 M35 M32 M30 A függvény jelölése: 3 37
33 5 3 2
0 M M M (0,2,5,7) M
f .
1.4 A logikai függvények egyszerűsítése
A negáció, konjunkció és diszjunkció függvényekre érvényesek a következő összefüggések (X, Y és Z bináris változók, azaz X,Y,Z{0,1}):
OR (+) AND ()
idempotencia XXX XX X 1
1
X X1X
X 0
X X00
kommutativitás XY YX XY YX
asszociativitás X(YZ)(XY)Z X(YZ)(XY)Z disztributivitás XYZ (XY)(XZ)
) Z X ( ) Y X ( ) Z Y (
X
1 X
X XX 0
X X
de Morgan-azonosságok XY XY XY XY elnyelési szabályok XX(XXYY)XX
Az itt felsorolt azonosságok felhasználásával átalakíthatók (egyszerűsíthetők) a negáció, konjunkció- és diszjunkció-függvényekkel felírt bonyolultabb logikai függvények.
Példa:
Z Y Z X Y X Z (X X) Y Z X Y X Z X Y Z X Y Z X Y
X
Y X Z X ) 1 Z ( Y X ) Y 1 ( Z
X
Az azonosságokkal való számolás igen körülményes, azért gyorsabb és áttekinthetőbb módszereket feljesztettek ki. Ilyen eszköz az ún. Karnaugh-tábla, amely lehet minterm- vagy maxterm-tábla. A táblában annyi cella szerepel, amennyi minterm illetve maxterm képezhető (ez a változók számától függ). A táblában 1-et írunk azokba a cellákba, melyeknek megfelelő minterm, illetve maxterm szerepel a függvény előállításában.
A Karnaugh-táblákban a változók értékeit az ún. Grey kódnak megfelelő sorrenben kell szerepeltetni.
Karnaugh-tábla kétváltozós függvények esetén Minterm-tábla:
X
\
Y 0 10 0 1
1 2 3
Például az f(X,Y) XYXYXY m20m12m23 függvény minterm-táblája:
X
\
Y 0 10 1 1 1 1
Karnaugh-tábla háromváltozós függvények esetén Minterm-tábla:
X
\
Y Z
0 0
0 1
1 1
1 0
0 0 1 3 2
1 4 5 7 6
Például az
X Y Z X Y Z X Y Z X Y Z
) Z , Y , X ( f
37 36 53
33 m m m
m
függvény minterm táblája:
X
\
YZ 00 01 11 100 1
1 1 1 1
Karnaugh-tábla négyváltozós függvények esetén Minterm-tábla:
XY
\
ZV 00 01 11 1000 0 1 3 2
01 4 5 7 6
11 12 13 15 14
10 8 9 11 10
Például az
X Y Z V X Y Z V X Y Z V )
V , Z , Y , X ( f
134 54
43 m m
m
függvény minterm táblája:
XY
\
ZV 00 01 11 1000 1
01 1
11 1
10
A Karnaugh-tábla jelentősége az, hogy segítségével „grafikus” egyszerűsítést lehet végrehajtani a az alábbiak szerint:
1. A táblában olyan 1-esekből álló, vízszintesen vagy függőlegesen összefüggő részeket (hurkokat) kell keresni, amelyek 2 hatvány (2,4,8,…) darab 1-est tartalmaznak.
2. Egy huroknak úgy feleltetünk meg formulát (konjunkciót), hogy a ponált és negált formában egyaránt szereplő változókat elhagyjuk, a többit pedig a hurokban szereplő cellák által meghatározott formában (ponált vagy negált) szerepeltetjük.
3. Egy cella több hurokban is szerepelhet.
4. A táblázat szemközti szélső celláit szomszédosak kell tekinteni a hurkok képzésénél.
Lehetséges hurkok kétváltozós függvény esetén:
X \ Y 0 1 X \ Y 0 1 X \ Y 0 1 X \ Y 0 1 X \ Y 0 1
0 1 1 0 1 0 1 0 0 1 1
1 1 1 1 1 1 1 1 1 1 1
X Y Y X 1
Lehetséges hurkok háromváltozós függvény esetén:
X\YZ 00 01 11 10 X\YZ 00 01 11 10 X\YZ 00 01 11 10
0 1 0 1 0 1
1 1 1 1 1 1
Z
Y YZ YZ
X\YZ 00 01 11 10 X\YZ 00 01 11 10 X\YZ 00 01 11 10 0 1 0 1 1 0 1 1
1 1 1 1
Z
Y XY XZ
X\YZ 00 01 11 10 X\YZ 00 01 11 10 X\YZ 00 01 11 10
0 1 1 0 0
1 1 1 1 1 1 1
Y
X XY XZ
X\YZ 00 01 11 10 X\YZ 00 01 11 10 X\YZ 00 01 11 10
0 0 1 1 0
1 1 1 1 1 1 1
Y
X XZ XZ
X\YZ 00 01 11 10 X\YZ 00 01 11 10 X\YZ 00 01 11 10 0 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1
Y Z Y
X\YZ 00 01 11 10 X\YZ 00 01 11 10 X\YZ 00 01 11 10 0 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1
Z X X
X\YZ 00 01 11 10
0 1 1 1 1 1 1 1 1 1
1 Példa:
Egyszerűsítsük a szavazógép logikai függvényét! A függvény igazságtáblázata és előállítása diszjunktív normálformában:
X Y Z f(X,Y,Z)
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1 XYZ
1 0 0 0
1 0 1 1 XYZ 1 1 0 1 XYZ 1 1 1 1 XYZ
Z Y X Z Y X Z Y X Z Y X ) Z , Y , X (
f
A függvény minterm táblája és az egyszerűsítéshez használt hurkok:
Z
X XY
Z Y
Az f függvény egyszerűsített formája ez alapján:
. Z Y Z X Y X ) Z , Y , X (
f
Négyváltozós esetben a lehetséges hurkok nagy száma miatt nem rajzoljuk fel az összes esetet, csak néhány jellegzetes 4, illetve 8 cellás hurok alakot.
XY\ZV 00 01 11 10 XY\ZV 00 01 11 10 XY\ZV 00 01 11 10 00 00 1 1 00 1 1
01 1 1 01 01
11 1 1 11 11
10 10 1 1 10 1 1 V
Y YZ YV
XY\ZV 00 01 11 10 XY\ZV 00 01 11 10 XY\ZV 00 01 11 10 00 1 1 00 1 1 00 1 1 1 1
01 1 1 01 1 1 01
11 1 1 11 1 1 11
10 1 1 10 1 1 10 1 1 1 1
V Z Y
Példa
Egyszerűsítsük az f függvényt, amelynek igazságtáblázata X Y Z V f(X,Y,Z,V)
0 0 0 0 1 XYZV 0 0 0 1
0 0 1 0 1 XYZV 0 0 1 1 1 XYZV 0 1 0 0
0 1 0 1 1 XYZV 0 1 1 0
0 1 1 1 1 XYZV 1 0 0 0 1 XYZV 1 0 0 1
1 0 1 0
1 0 1 1 1 XYZV 1 1 0 0 1 XYZV 1 1 0 1
1 1 1 0 1 1 1 1
X Y Z V X Y Z V X Y Z V X Y Z V
) V , Z , Y , X ( f
V Z Y X V Z Y X V Z Y X V Z Y
X
A függvény minterm táblája és az egyszerűsítéshez használt hurkok:
V Z X
V Y X V
Y X
V Z Y
Az f függvény egyszerűsített formája ez alapján:
. V Y X V Y X V Z Y V Z X ) V , Z , Y , X (
f
2. KOMPLEX SZÁMOK
2.1 A komplex számok különféle alakjai, elnevezések
algebrai alak: abi a,b
trigonometrikus alak: r(cosisin) r, , r0 exponenciális alak: rei r, , r0 A komplex számok ábrázolása,
komplex számsík:
: a komplex számok halmaza i: képzetes egység
a: valós rész (Re(z)) b: képzetes rész (Im(z)) r: hossz, abszolút érték (|z|)
: szög/argumentum (arg(z)) z: komplex konjugált
2.1 ábra: Komplex számsík Kapcsolat a komplex szám jellemzői között:
r sin
a z r a2 b2,
r cos
b .
a tg b
Megjegyzések:
1. A képzetes egységet sokszor j-vel jelölik. A „Számolás váltakozóáramú hálózatokban”
című részben mi is ezt tesszük, hogy a képzetes egység és az áramerősség jele ne egyezzen meg.
2. A z abi komplex számot a z abi komplex szám konjugáltjának nevezzük.
3. Bizonyos számolásokban z komplex számot azonosítják a komplex számsíkban az origóból a z-nek megfelelő pontba mutató vektorral. E vektor „koordinátái” a komplex szám valós és képzetes része.
4. Egy komplex számhoz a [0,2[ tartományból egyértelműen hozzárendelhető szög. A komplex számokkal való számolásokban gyakran adódnak más szögértékek is.
Ilyenkor – tekintettel a sin- és a cos-függvények 2 szerinti periodicitására – a szöghöz hozzáadható a 2 érték egész számszorosa (k 2, k ), amivel megkapható a [0,2[ tartományba tartozó szögérték.
5. Mivel a tangens függvényperiódusa , azaz a [0,2[ intervallumon minden értéket kétszer vesz fel, önmagában a b/a hányados nem határozza meg egyértelműen a komplex szám szögét.
2.2 Alapműveletek, hatványozás, gyökvonás
Az összeadás és a kivonás az algebrai, a szorzás, osztás, hatványozás és a gyökvonás a trigonometrikus és az exponenciális alakban végezhető el könnyebben.
Összeadás és kivonás
a1b1i
a2 b2i
a1a2
b1b2
,i
a1b1i
a2 b2i
a1a2
b1b2
.i (E műveletek megfelelnek a vektorok összeadásának és kivonásának.)i b a z1 1 1
i b a z2 2 2
i ) b b ( ) a a ( z
z1 2 1 2 1 2
2.2 ábra: Komplex számok összeadása
2 1
) sin i (cos r
z1 1 1 1 ) sin i (cos r
z2 2 2 2
2 1 z z 2
1 z z
2 1
2.3 ábra: Komplex számok szorzása Szorzás, osztás és pozitív egész kitevős hatványozás
cos( ) i sin( )
; rr ) sin i (cos r ) sin i (cos
r1 1 1 2 2 2 1 2 12 12
cos( ) i sin( )
; rr ) sin i (cos r
) sin i (cos r
2 1 2
1 2
1 2 2
2
1 1
1
r(cosisin)
n rn
cos(n)isin(n)
(n pozitív egész szám).Megjegyzés: ii=i2=-1.
Gyökvonás
Tekintettel arra, hogy a szöget a 2 egész számú többszörösével (k 2,k ) megváltoztatva ugyanazt a komplex számot kapjuk, könnyen belátható, hogy adott z 0 komplex szám esetén a zn r(cosisin) egyenletnek (n pozitív egész szám) n darab különböző megoldása van: azok a komplex számok, melyek hossza nr , szöge pedig a
n ) 2 1 n n ( ,..., n 2 2 ,n n 2 ,n n
szögek valamelyike.
Így minden z 0 komplex számnak n darab különböző n-edik gyöke van, melyek az origó középpontú, nr sugarú körön, egy szabályos n-szög csúcsaiban helyezkednek el a komplex számsíkban:
. 1 n ,..., 2 , 1 , 0 k n ,
k 2 sin n n i
k 2 cos n r ) sin i (cos
r n
n
Komplex exponenciális függvény
Az exponenciális alak a komplex exponenciális függvénnyel van felírva, amely az
0 n z n
! n
e z , z
hatványsorral van definiálva.
Ha a z komplex változó (kitevő) helyett az x valós változó szerepel, akkor a valós exponenciális függvényt kapjuk: ex
n0(xn/n!), x . Tisztán képzetes kitevő esetén a függvényértékek komplexek, amelyekben (a képzetes tengely irányában) 2 szerinti periodikusság mutatkozik. A periodikusság jól látható az ei cosisin Euler- formulából, mely a tisztán képzetes kitevőjű exponenciális és a valós szinusz- és koszinusz függvények közti összefüggés. Érdekes a = esetén adódó ei10 összefüggés az alapvető matematikai konstansok között.A szorzás, osztás és a pozitív egész kitevős hatványozás exponenciális alakban:
, e
r r e r e
r1 i1 2 i2 1 2 i(12) e , r
r e r
e
r i( )
2 1 i 2
i
1 1 2
2
1
rei
n rnei(n)(n pozitív egész szám).
2.3 Számolás váltakozóáramú hálózatokban
Az elektromosságtanban feltételezzük, hogy az ún. passzív áramköri elemekből (ohmos ellenállásból, kondenzátorból és tekercsből) álló rendszerek lineárisak, így teljesül a szuperpozíció elve. A linearitás, valamint a Fourier-elmélet alapján megállapítható, hogy a periodikus időfüggvényű feszültséggenerátorok (ill. áramgenerátorok) felfoghatók harmonikus (szokásos szóhasználattal élve: szinuszos) időfüggvényű feszültséggenerátorok (ill. áramgenerátorok) soros kapcsolásaként. Ennek alapján a periodikusan gerjesztett, csak passzív elemeket tartalmazó áramkörök vizsgálata a harmonikus gerjesztésű rendszerek elemzésén alapul.
Az elektromosságtanból tudjuk, hogy a passzív áramköri elemek feszültsége és árama színuszos gerjesztés esetén az alábbiak szerint függ össze (az egyszerűbb áttekinthetőség érdekében a feszültségfüggvény esetén nulla fázisszöget feltételezünk).
Ellenálláson (R)
Feszültség u(t)U0sin(t)
Áramerősség sin( t)
R ) U t sin(
I ) t (
i 0 0 R
/ U I0 0 Fáziseltolódás =0 Kondenzátoron (C)
Feszültség u(t)U0sin(t)
Áramerősség
U C sin t 2
t 2 sin I ) t (
i 0 0
C U I0 0 Fáziseltolódás
2
, az áram „90°-kal siet” a feszültséghez képest
Tekercsen (L)
Feszültség u(t)U0sin(t)
Áramerősség
sin t 2
L U t 2
sin I ) t (
i 0 0
) L /(
U I0 0 fáziseltolódás
2
, az áram „90°-kal késik” a feszültséghez képest
A váltakozóáramú hálózatokban végzett számítások szempontjából fontos megjegyezni, hogy míg ohmos ellenállás esetén a feszültség és az áramerősség pillanatnyi értékeinek hányadosa bármely időpillanatban megegyezik az egyenáramú ellenállással
0 0
I U ) t ( i
) t (
R u , addig a kondenzátor és a tekercs esetén ez a hányados az körfrekvencia függvénye, és nem hordoz közvetlen fizikai jelentést.
Számolások egyszerűsítése végett a váltakozóáramú hálózatokban a feszültséget és az áramerősséget komplex értékű függvényekkel írjuk le (az idő függvényében). E függvények hányadosa az időtől független állandó, a komplex impedancia, vagy másképpen komplex váltakozóáramú ellenállás.
A komplex függvények alkalmazásának egyik előnye, hogy az egyenáramú körökben használt összefüggések (pl. a Kirchhoff-törvények) érvényben maradnak. Az alábbiakban összefoglaljuk a számításokban előforduló komplex értékű függvényeket és ezek összefüggéseit.
A feszültség–idő függvény leírása komplex formában
Ebben a részben a képzetes egységet j, a mennyiségek komplex értékeit ~ jelöli.
A feszültség időbeli változását leíró u(t)U0sin(tU) függvény az
U U
0 j( t )0 cos( t ) j sin( t ) U e U
U ) t (
~u
az ún. komplex feszültségfüggvény képzetes része: u(t)Im
~u(t).Ahhoz, hogy a U fázisszög (konstans) és az időtől függő t tag szerepét megkülönböztessük, az exponenciális kifejezést szétbontjuk:
. e U~ e
e U e
U ) t (
~u j t
t 0 j j
) 0 t (
0 j U U
Az ~U0 U0 ejU
komplex számot a feszültségfüggvény komplex amplitúdójának nevezzük. Mivel ejU 1, a komplex amplitúdó nagysága megegyezik az U0 valós amplitúdóval (maximális feszültséggel), emellett tartalmazza a U fázisszöget is.
Az áramerősséghez ugyanezen az elven rendelünk komplex függvényt: az )
t sin(
I ) t (
i 0 I függvény szerint változó áramerősséghez rendelt komplex áramerősség-függvény:
cos( t ) j sin( t )
I e .I ) t (
~i j( t )
0 I I
0 I
A valós áramerősség-függvény a komplex áramerősség-függvény képzetes része:
~i(t)Im ) t (
i . Az áramerősség-függvény komplex amplitúdója: ~I0 I0 ejI
, ezzel .
e
~I e
e I e
I ) t (
~i j t
t 0 j j
) 0 t (
0 j I I
A fentiek alapján a komplex amplitúdó nagysága megegyezik az I0valós amplitúdóval (maximális áramerősséggel), emellett tartalmazza a fázisszöget is.
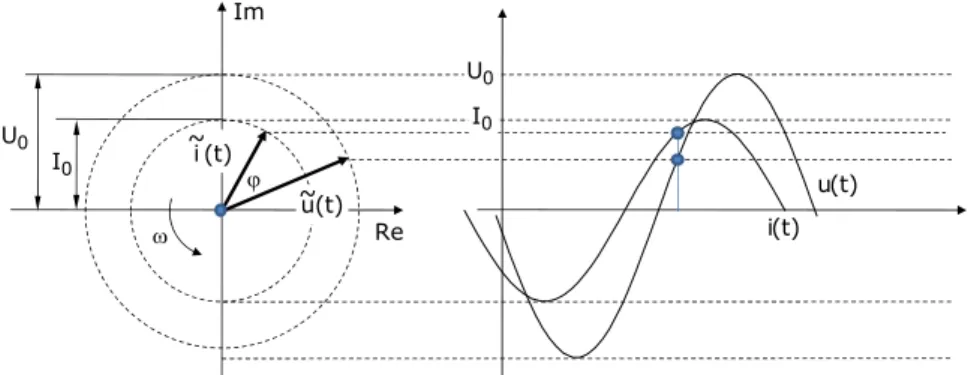
A komplex feszültség- és áramerősség-értékek a komplex számsíkban vektorokként ábrázolhatók, amelyek harmonikus gerjesztés esetén szögsebességgel egyenletes körmozgást végeznek az origó körül. A vektorok által bezárt szög a feszültség és az áramerősség fázisának eltérése.
U0
I0
Re Im
) t (
~i
) t (
~u
U0 I0
) t ( i
) t ( u
2.4. ábra: Komplex feszültség- és áramfüggvények Impedancia
Egy passzív áramköri elem impedanciája az elem komplex feszültség- és áramerősség- amplitúdójának hányadosa:
. I e
U e
I e U
~I U~
Z~ j( )
0 0 j
0 j 0 0
0 U I
I
U
Az impedancia tehát a feszültség és az áramerősség maximális értékétől, valamint a fázisszögek eltérésétől függ. A három áramköri elem esetén, a fentiek alapján:
Áramköri
elemek UI
) ( j 0
0 e U I
I Z U
~
0 0
I Z U
Ellenállás 0 ~Z R ej0 R
R R
Kondenzátor
2
j X j
C e 1
C Z 1
~ j2 C
C
C 1
Tekercs
2
~Z L e L j X j
2 L j
L
L
Megjegyzések
1. A komplex impedancia ohmos ellenállás esetén pozitív valós szám, kondenzátor és tekercs esetén tisztán képzetes (negatív, illetve pozitív előjellel).
2. Az ellenállás impedanciája nem függ az gerjesztési körfrekvenciától, míg a kondenzátoré csökken, a tekercsé pedig növekszik az növekedtével. Emiatt különböző gerjesztési frekvenciákra egy adott áramkör másképpen reagál.
3. A kondenzátor és a tekercs impedanciájának nagyságát látszólagos ellenállásnak is hívjuk.
A valós impedancia a komplex impedancia nagysága:
I . e U
I e U
I Z U Z ~
0 ) 0 ( j 0 ) 0 ( j 0
0 U I U I
A komplex feszültség- és áramerősség-amplitúdókkal érvényes az Ohm törvény és a Kirchhoff-törvények:
Ohm-törvény: ~ ~ ~.
0
0 I Z
U Csomóponti törvény: ~ ~0.
0
nI n
Huroktörvény: ~ ~0.
0
nU n
L
C 1
~zC Im
L 1
~ZRe R
~Z
valóstengely
tengely képzetes
2.5 ábra: Ellenállás, kondenzátor, tekercs impedanciája
Soros és párhuzamos kapcsolásnál a komplex impedanciákra érvényesek az egyenáramú körökben is használ összefüggések. Sorosan kapcsolt, 1 ~Zn
,...,
~Z
impedanciájú elemek eredő impedanciája:
.
~Z ...
~Z
~Z
n soros 1
,
eredő
Párhuzamosan kapcsolt, 1 ~Zn ,...,
~Z
impedanciájú elemek eredő impedanciájára:
n párhuzamos 1
,
eredő ~Z1
Z ...
~1
~Z 1
.
Ha a kapcsolás ellenállás mellett kondenzátort és/vagy tekercset is tartalmaz, akkor eredő impedancia valós és képzetes részt egyaránt tartalmaz. Az összetevőket a komplex számsíkban ábrázolva jól látható az egyes impedanciák hatása az eredőre (2.5 ábra).
Soros RC kapcsolás esetén például az alábbiak szerint alakulnak a függvények és összefüggések:
Generátorfeszültség:
valós feszültségfüggvény: ug(t)Ug0sin(t);
komplex feszültségfüggvény: u~g(t)Ug0ejt;
komplex feszültségamplitúdó: U~ U .
0 g 0
g
Eredő impedancia:
C .j R 1
Z~ Z~ Z~
C R
RC
A körben folyó áram:
komplex áramerőssé amplitúdó: ;
C j R 1
U Z~
U~
~I g0
RC 0 g
0
valós áramerősség-amplitúdó: ;
C R 1
I U I ~
2 2
0 g 0
0
komplex áramerősség-függvény:
2 jt
2 0 t g
0 j t g
0 j j e
C R 1 C R 1
e U C j R 1 e U
~I ) t (
~i
, e I e
C R 1
e U C e
R 1 C
R 1
U j( t )
0 ) t ( j 2 2
0 t g
j j 2 2
2 2
0
g
ahol: 0
C R
1 RC
1
tg
, így
0 2
, az áramerősség „siet” a generátor- feszültséghez képest (kapacitív jellegű kapcsolás);
valós áramfüggvény:
~i(t) Im
I e
Im
I
cos( t ) j sin( t )
I sin( t ).Im ) t (
i 0 j(t) 0 0 Az áramköri elemek feszültsége
komplex feszültségamplitúdók: R,
C j R 1
Z U I ~
U~ ~ g0
R 0 0
R
; C j 1 C j
R 1 Z~ U
~I
U~ g0
C 0 0
C
valós feszültségamplitúdók: R I R,
C R 1
U~ U
U 0
2 2
0 g 0
R 0
R
; X C I
1
C R 1
U~ U
U 0 C
2 2
0 g 0
C 0
C
komplex feszültségfüggvények:
2 jt
2 0 t g
0 j t g
0 j R
R j e
C R 1 R C R 1
e U R C j R 1 e U
U~ ) t (
~u
, e
R I e
R C R 1
e U C e
R 1 R C R 1
U j( t )
0 ) t ( j 2
2 0 t g
j j 2 2
2 2
0
g R R R
ahol:
C R tg R 1
. Mivel R (lásd előbb a komplex áramerősség-függvényt), az ellenállás árama fázisban van az ellenállás feszültségével: ~uR(t)I0Rej(t).
C0 jt g0 jt
C j e
C 1 C j
R 1 e U
~U ) t (
~u
2 jt
2 0 t g
j 2 2
0
g j R e
C 1 C 1 C
R 1 e U
C j R 1 C j
1 C
R 1 U
2 j jt
2 2 2
0
g R e e
C 1 C
1 C
R 1
U C
, e
R I C e
1
C R 1
U j( t )
0 ) t ( j 2
2 0
g C C
ahol:
tg 2
tg 1 C 1
tg C R , azaz
C 2
, így a kondenzátor feszültsége
„90°-kal késik” az áramához képest:
0 j t 2
C(t) I R e
~u ;
valós feszültségfüggvények:
R 0 j(t)
R(t) Im~u (t) ImI R e u
I R cos( t ) j sin( t )
I R sin( t );Im 0 0
t 2
j 0 C
C(t) Im~u (t) Im I R e u
2 . t
sin R 2 I
t sin 2 j
t cos R I
Im 0 0