Válaszok a Dr. Szabó Péter János

1

Válaszok a Dr. Szabó Péter Jánoskérdéseire Tisztelt Bíráló!

Köszönöm szépen a munkám elbírálását, a konstruktív megjegyzéseket és az érdekes kérdéseket!

A felmerült kérdésekre (megjegyzésekre) legjobb tudásom szerint válaszoltam.

Kérdések és válaszok

1. kérdés. Hogyan jött ki ez a formula (3.10. összefüggés)?

Válasz





3 / 4 1/ 2 3 / 4 1/ 2

h h h h h h

h h

h h h h

+ +

+ +

− − − − (3.10)

Az összefüggés úgy jött ki, hogy észrevettem, hogy a -szál mentén a h, k, l indexek között a következő összefüggések vannak: h= egész szám, k=1 (ha nagyobb vagy kisebb az egynél, akkor ilyen tényezővel meg kell szorozni a h-t és az l-t ), és l=h+k.

Ez a szabály érvényes az összes komponensre a -szál mentén: (1 1 2)[-1 -1 1], vagy (3 1 4)[-5 -9 6], vagy (1 0 1)[-1 -2 1].

Az u, v, w indexek meghatározása bonyolultabb összefüggést mutatnak ki, viszont mindegyik index a h index függvénye és ez könnyítette a munkát. Kihasználva a hu+kv+lw=0 kristálytani alapszabályt, ismerve h, k, l, u és v indexeket a w index automatikusan meghatározható.

A 3. 10 képlet megfelel a kristálytani alapszabálynak (hu+kv+lw=0):

2 2 2 2

( 1) 2 ( 1) ( 1) 2 ( 1) ( 1) 2 ( 1) ( 1) 2 ( 1)

3 / 4 1 / 2 3 / 4 1 / 2 3 / 4 1 / 2 3 / 4 1 / 2 0

h h h h h h h h h h h h h h h h

h h h h h h h h

+ + + + + − + = + + + − + − + =

− − − − − − − −

A 3. 10 összefüggés érvényes az egész Euler térre, és az összes h, k, l, u, v, w Miller indexekre. Például h=1 esetén a 3.10 képlet megadja az (1 1 2)[-8 -8 8] 

(1 1 2)[-1 -1 1] komponenst, h=3 esetén megkapjuk a (3 1 4)[ -48/9 -96/10 576/90]  (3 1 4)[-5 -9 6] komponenst, és a végtelen nagy szám esetén, pl. h=10²⁵, megkapjuk (10²⁵ 1 10²⁵)[- 10²⁵ -2x10²⁵ 10²⁵]-t és elosztva 10²⁵ -tel megkapjuk

 (1 0 1)[- 1 -2 1].

2

2. kérdés. Az FLM módszer validálásánál a Pályázó részletesen leírja a modellben szereplő  és n paraméterek meghatározását. Ezzel kapcsolatban két kérdést fogalmaztam meg:

Mi az  és az n paraméter jelentése, megfogalmazható-e ez valamilyen fizikai tartalom segítségével, vagy csak matematikai segédmennyiségek?

Válasz

Az FLM módszer definiálja az anyagáramlási vonalakat, amelyek a sebességirányokat határozzák meg a különböző mélységű rétegekben. Ahhoz, hogy bevezessük az anyagáramlás vonalak menti sebességek közötti különbségeket, két modell paramétert alkalmazunk ( és n). Az  és n paraméterek egyaránt matematikai segédmennyiségek, viszont ahogy a 4.17-4.19 képletek mutatják, mind a két mennyiség a rés geometria és a súrlódási tényező  függvénye. Az  definiálja az x-z elmozdulás mértékét, és az n meghatározza az elmozdulási profil alakját.

2 3 4

2

i f

h h

A B C D E

=  +  +  +  + ^{ −}L ^

 , (4.17)

k l

g

f i

i f f

h R R

R h h h

 = ^{ }    ^ − ^{ }    ^ , (4.18)

u w y

s

i f

r i t v x

dN i f

h h

h L L

n M N O P Q

R L R h h

 ^{ }  ^{ }  ^{ + }  ^{ }

=    +   +   +  +  + , (4.19)

3

A 4.17-4.19 képletek alkalmazásával olyan eredményt kapunk, mely összehasonlító a végeselem szimulációval (pl. 4.10 ábra az értekezésben).

Fig. 4.10. Grid distortions predicted for various roll gap geometries [3s] by the FLM employed and FEM. The FLM model parameters were calculated by eqs. 4.17-4.19.

4

3. kérdés. A 4.17-19. egyenletekben felsorolt paraméterek (22 db) hogyan, miből kerültek meghatározásra?

Válasz

A 4.17-19. egyenletekben felsorolt 22 db paraméter (A-y) úgy lett meghatározva, hogy:

1. mindegyik VEM szimuláció után elvégeztem az FLM számitást, és az  és n paraméterek változásával próbáltam reprodukálni a végeselem által megkapott elmozdulási profilt (az alábbi ábra (=0,134 és n=1,64) vagy 4.10 ábra az értekezésben). Összesen 53 VEM által kiszámolt elmozdulási profilra meghatároztam az optimális  és n paramétereket.

2. A második lépésben figyeltem, hogy milyen hatással vannak a hengerlési paraméterek (, R, Ld, , hi) az  és n modell paraméterekre. Szeretném kiemelni, hogy a képleteknek nincs analitikai levezetése, az összefüggések empirikus, tapasztalati megfigyeléseken alapulnak. Így kidolgoztam a 4.17-4.19 képleteket és utána a 22 db paramétert (A-y) illesztettem az Excel „GRG-nonlinear” módszerének felhasználásával.

A 4.17-4.19 képletek által számolt ( - számolt és n-számolt) és optimális ( - optimális és n – optimális) paraméterek közötti összefüggés látható az alábbi ábrákon.

5

4. kérdés. A 4.2.2. fejezetben a lemez vastagsága mentén átlagos textúrákkal számol, illetve ezt modellezi, a 4.2.3. fejezetben pedig a lemezvastagságot 3 részre osztja, figyelembe véve a kiindulási lemez vastagság menti textúra-inhomogenitását és a hengerlés hatásának mélységfüggését.

Kérdésem: Vajon ettől eltérő eredményre számíthatnánk-e akkor, ha az ND síkon végeznénk az EBSD-méréseket úgy, hogy az előző mérésnél meghatározott három réteg vastagságának megfelelő anyagmennyiséget eltávolítanánk az ND síkról, és így haladnánk (rétegenként) a középső réteg felé?

Válasz

A kísérleti eredmények arra utalnak, hogy szintén azonos textúrákat kapunk, ha az ND síkon végezzük a textúra-méréseket úgy, hogy az előző mérésnél meghatározott három réteg vastagságának megfelelő anyagmennyiséget eltávolítjuk az ND síkról, és így rétegenként haladunk a középső réteg felé. Az alábbi ábrák arra utalnak, hogy mind a két módszer alkalmazható és azonos eredményre vezet.

Három ND síkon (felület, felület alatti és középréteg) mért és utána egyesített textúra 6016 Al ötvözetben aszimmetrikus hengerlés után és Alamel által modellezett textúra.

A lemez vastagsága mentén mért textúra 6016 Al ötvözetben (h=1mm).

Három ND síkon (felület, felület alatti és középréteg) mért és utána egyesített textúra 6016 Al ötvözetben.

Mért Alamel modell

Aszimmetrikus hengerlés

6

5. kérdés. Az 5.3. ábrán megfigyelhető, hogy a kisebb alakítás után egyfajta bimodális szemcseszerkezet jött létre (kicsi és nagy szemcsék), a nagyobb alakításoknál ez az inhomogenitás kevésbé, vagy egyáltalán nem figyelhető meg. Az ábrából nem látszik, hogy ez a részleges újrakristályosodásnak az eredménye, de feltételezhető, hogy igen. Kérdésem ezzel kapcsolatban:

Van-e kimutatható különbség az aprószemcsés és a durvább szemcsés tartományok textúrája között?

Válasz

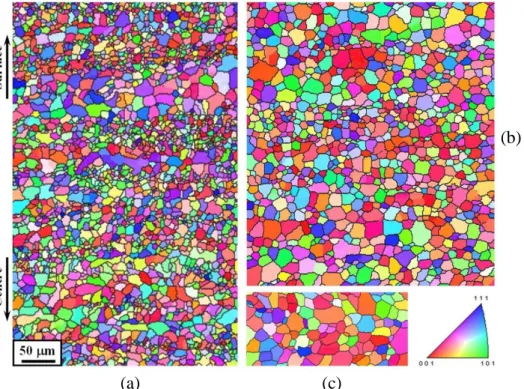
Mind a három esetben (a-c) az újrakristályosodás befejeződött. A bimodális szemcseszerkezet (5.3 a ábra) az inhomogén részecske/kiválás (1-3 mikrométeres) eloszlásának következménye. A durvaszemcsés szerkezet az úgynevezett „részecske indukált újrakristályosodási mechanizmusnak” (PSN, particle stimulated nucleation) az eredménye. A finom és a durvaszemcsés rétegek különböző textúrákkal rendelkeznek (ld. az alábbi ábrát), mivel az újrakristályosodási mechanizmusok eltérnek a kemény/rideg részecskék környezetében (particle affected deformation zone, PADZ), és a kiválások nélküli Al mátrixban (5.3 ábra). A PADZ nagy hajtóerőt biztosit a szemcsecsírák számára (5.9 ábra), és így durvaszemcsés szerkezet keletkezik specifikus textúrával: P-komponens ((011)[23-3]) , -szál közeli komponensek és (001)[110].

(b)

Fig. 5.3. Inverse pole figure maps (TD-plane, the scale bar is || to RD) of Al-2.8Mg alloy recrystallized at 550°C for ~4 seconds after various rolling reductions: a) ~85.0% reduction;

b) 96.9% reduction; c) 99.1 % reduction. The maps are of the same scale [2s].

(a) (c)

7

Szombathely, 2021/06/14 Dr. Sidor Jurij

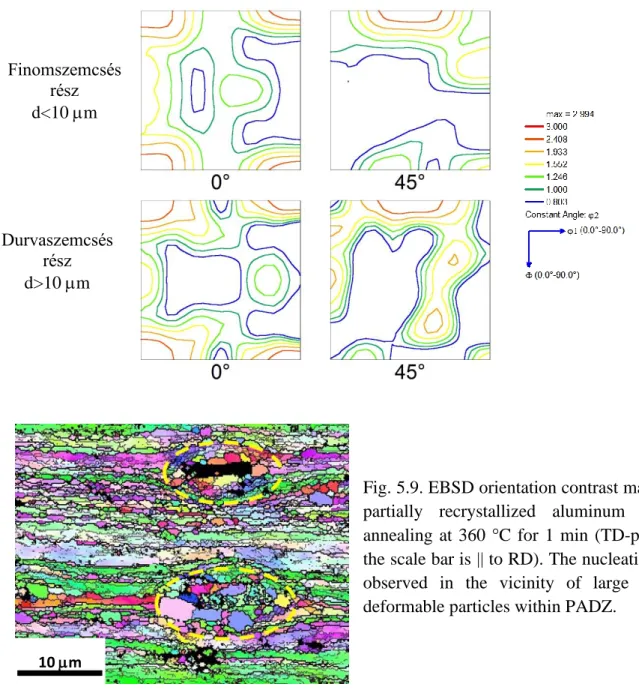
Finomszemcsés rész d<10 m

Durvaszemcsés rész d>10 m

Fig. 5.9. EBSD orientation contrast map of partially recrystallized aluminum after annealing at 360 °C for 1 min (TD-plane, the scale bar is || to RD). The nucleation is observed in the vicinity of large non- deformable particles within PADZ.

10 m