Matematikai geodéziai számítások 9.

(1)

Matematikai geodéziai számítások 9.

Szabad álláspont kiegyenlítése

Dr. Bácsatyai, László

(2)

Created by XMLmind XSL-FO Converter.

Matematikai geodéziai számítások 9.: Szabad álláspont kiegyenlítése

Dr. Bácsatyai, László Lektor: Dr. Benedek , Judit

Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 „Tananyagfejlesztéssel a GEO-ért” projekt keretében készült.

A projektet az Európai Unió és a Magyar Állam 44 706 488 Ft összegben támogatta.

v 1.0

Publication date 2010

Ez a modul a mérőállomásokban opcionálisan jelenlévő szabad álláspont meghatározás közvetett mérések szerinti kiegyenlítését és a megbízhatósági mérőszámok meghatározását mutatja be.

Jelen szellemi terméket a szerzői jogról szóló 1999. évi LXXVI. törvény védi. Egészének vagy részeinek másolása, felhasználás kizárólag a szerző írásos engedélyével lehetséges.

(3)

Tartalom

9. Szabad álláspont kiegyenlítése ... 1

1. 9.1 A feladat megfogalmazása ... 1

2. 9.2 Szabad álláspont meghatározása ... 2

3. 9.3 Számpélda ... 7

(4)

(5)

9. fejezet - Szabad álláspont kiegyenlítése

1. 9.1 A feladat megfogalmazása

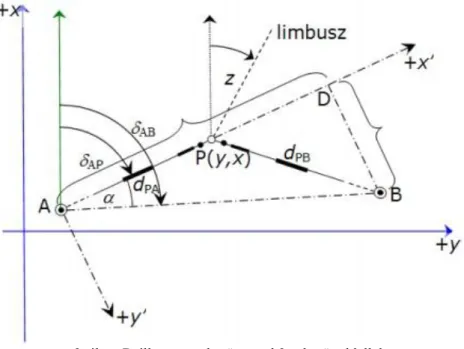
1. ábra

Az ábrán látható hálózatban adottak az A és B pontok vetületi koordinátái. Mértük az irányokat és a távolságokat, valamint ismerjük a mérési eredmények előzetes középhibáit, a és a értékeket.

Meghatározandók:

• a P pont koordinátái és a z tájékozási szög közelítő értékei,

• a javítási egyenletrendszer,

• a mérési eredmények súlymátrixa,

• a normálegyenlet rendszer együtthatómátrixa és a tisztatag vektor,

• a P pont koordinátái és a tájékozási szög kiegészítő értékei,

• a P pont kiegyenlített koordinátái m-ben és a tájékozási szög kiegyenlített értéke,

• a mérési javítások és kiegyenlített mérési eredmények,

• a súlyegység középhibája és az ismeretlenek kiegyenlítés utáni középhibái.

A normál-egyenletrendszer megoldásához szükséges inverz mátrixot az adjungált mátrix segítségével kell meghatározni.

Dimenziók:

• szögmásodpercben: részben a javítási egyenletek tisztatagjai, a tájékozási szög kiegészítő értéke,

• mm-ben: részben a javítási egyenletek tisztatagjai, mérési javítások, a P pont koordinátáinak kiegészítő értékei, a kiegyenlített ismeretlenek középhibái,

• m-ben: a P pont koordinátáinak közelítő értékei és kiegyenlített koordinátái.

Az itt fel nem sorolt mértékegységek megtalálhatók a mintapéldában.

(6)

Szabad álláspont kiegyenlítése

2

Leadandók különálló borítólapba foglalva:

• A feladatkiírás és a kiinduló adatok (feladatlapba foglalva),

• Számítások listája a rész- és végeredményekkel együtt,

A feladatot, a felhasznált képletekkel és tájékoztató szöveges információkkal együtt – különálló borítólapba foglalva - kézzel írott, vagy Microsoft Word formátumban kell leadni.

2. 9.2 Szabad álláspont meghatározása

Tudjuk, hogy a szabad álláspont meghatározásakor a meghatározandó ponton a mérőállomással belső irányokat és távolságokat mérünk az ismert pontokon felállított prizmákra. Ha csak belső irányokat mérnénk, legalább 3 belső irány esetén hátrametszésről, 2 belső irány és 2 távolság esetén pedig a beillesztett sokszögvonal egy speciális esetéről beszélnénk, nevezetesen arról, amikor a 2 adott pont közötti egyetlen sokszögpontról mérünk irányt és távolságot a sokszögvonal kezdő- és végpontjára (ábra). Természetesen, a szabad álláspontnak még egyéb variációi is elképzelhetők. A szabad álláspont koordinátáit a mérőállomás mikroszámítógépe számítja, a felhasználó már csak a kész eredményeket olvassa le, ill. rögzíti.

2. ábra: Beillesztett sokszögvonal 2 sokszögoldallal

3 belső irány esetén nincs fölös mérésünk, 2 belső irány és 2 távolság esetén a mérési eredmények száma n = 4, a meghatározandó ismeretlenek száma pedig m = 3, a pont két koordinátája és a tájékozási szög. A fölös mérések száma n – m = 1, tehát fennáll a kiegyenlítés feltétele. Válasszuk mintapéldaként ezt az egyszerű esetet!

Fejezzük ki a mérési eredményeket a meghatározandó ismeretlenek függvényében!

Közvetítő egyenletek az iránymérésekre:

;

.

Közvetítő egyenletek a távolságmérésekre:

(7)

;

.

A fenti egyenletekben ismeretlenek az álláspont koordinátái és a z tájékozási szög.

Legyenek még adottak a mérési eredmények és előzetes középhibái, azaz eltekintünk attól, hogy az elektronikus távmérés pontossága függ a mért távolságtól.

A koordináták közelítő értékeit^∗ a fenti ábra alapján, a beillesztett sokszögvonal számításának megfelelően kapjuk. A sokszögvonal AB záróoldalának irányszöge:

.

induló irányszöggel számítjuk a sokszögvonalat, ill. a sokszögoldal összegek tengely-irányú komponenseit az y’, x’ segédkoordináta-rendszerben, majd meghatározzuk az α szöget:

.

A irányszög:

3. ábra: A

irányszög számítása

A irányszög: .

A irányszög:

A koordináták közelítő értékei:

.

∗ A sorba fejtés korlátai miatt itt feltétlenül szükséges jó közelítő értékek bevezetése!

(8)

4

A z tájékozási szög közelítő értéke: .

Képezzük az alábbi parciális deriváltakat:

;

. A javítási egyenletek:

(9)

;

; . A javítási egyenletek tiszta tagjai:

;

. A megoldás:

;

, ahol

az ismeretlenek kiegészítő értékeit;

a keresett ismeretleneket;

pedig az ismeretlenek közelítő értékeit;

(10)

6

a javítási egyenletek tisztatagjait tartalmazza.

Továbbá

a javítási egyenletrendszer együttható mátrixa;

a súlymátrix;

a normálmátrix; a tisztatagok vektora. A P mátrixról feltételezzük, hogy az egyes mérési eredmények egymástól függetlenek.

Megbízhatósági mérőszámok:

Kofaktor-, vagy súlykoefficiens mátrix:

. Kovariancia-mátrix:

.

A keresett ismeretlenek utólagos középhibái:

.

j = 1, 2, 3, a mátrix j - ik főátló-beli eleme, a μ0 pedig a súlyegység utólagos középhibája. A mátrix nem diagonális, hiszen a matematikai megoldás az ismeretlenek között korrelációkhoz vezet.

A súlyegység középhibája:

(11)

,

mert most f = 4 – 3 =1 a fölös mérések száma. A μ0 értékénekszámításához szükség van a vektorra. Ennek számítása a vektor ismeretében a

javítási egyenletrendszer figyelembe vételével történhet.

3. 9.3 Számpélda

Adott pontok koordinátái:

Pontszám y (m) x (m)

A 457403,26 259799,79

B 458170,52 259654,24

Mérési eredmények:

A mérési eredmények előzetes középhibái:

; .

1. Közelítő értékek számítása:

;

(12)

8

;

. A koordináták közelítő értékei:

; . A z tájékozási szög közelítő értéke:

. 2. A javítási egyenletrendszer együttható mátrixa:

Az mátrix A(1,1), A(1,2), A(2,1) és A(2,2) elemeinek dimenziója ”/mm, ha a távolságokat mm-ben helyettesítjük be. A többi elemnek nincs dimenziója.

3. A javítási egyenletrendszer tisztatagjai:

(13)

Az l1 és l2 elemek dimenziója szögmásodperc (”), az l3 és l4 elemek dimenziója mm.

4. A javítási egyenletek:

;

.

A megállapodott dimenzióknak megfelelően az első két egyenlet tagjai ”, a 3. és 4. egyenlet tagjai mm dimenziójúak.

5. A súlymátrix:

.

A súlyok meghatározásánál a súlyegység középhibájának -öt választottunk, ahonnan

De , ezért a súlymátrix főátlójának első két eleme . A

(14)

10

távolságmérés előzetes középhibája A főátló utolsó két eleme ekkor - mellett -

.

6. A normál egyenletrendszer együttható-mátrixa és a tisztatag vektor:

; 7. A normál egyenletrendszer megoldása:

. 8. Adjungált mátrix képzése:

a) Az mátrix elemeihez tartozó aldeterminánsok:

b) Az aldeterminánsokból képzett mátrix: .

c) Az eredeti mátrix determinánsa:

(15)

d) Az inverz mátrix: .

9. A keresett ismeretlenek kiegészítő értékei:

. A két első kiegészítő érték dimenziója mm, a harmadiké szögmásodperc ”.

10. Kiegyenlített ismeretlenek (a P pont koordinátái m-ben és a tájékozási szög ”-ben):

.

11. Mérési javítások és kiegyenlített mérési eredmények:

; .

Az 1. és 2. mérési javítás ”, a 3. és 4. mérési javítás mm dimenziójú.

12. Megbízhatósági mérőszámok:

; A súlyegység középhibája: . Az ismeretlenek kiegyenlítés utáni középhibái:

; .

Irodalomjegyzék

Bácsatyai László: Kiegyenlítő számítások, elektronikus jegyzet pdf formátumban, NYME Geoinformatikai Kar, Székesfehérvár,