I I .
HUNGARY 1972
OMKDK-TECHNOINFORM
MAŰYAK lUÍOMÁXYOS AKADÉMIA
KONYVTÁHA
Distribution:
OMKDK TECHNOINFORM BUDAPEST 8. P.O.B. 12.
HU N G ARY
Felelős kiadós M a rx G y ö rg y
Készült az O M K D K házi sokszorosító üzem ében Budapest, V III. Reviczky u. 6..
Felelős ve ze tő : Janoch G yu la
IuD. 1 11 AivA j
Könyviéit ■ / o G L Ű m l - * -
T . D e G r a a f ( G r o n i n g e n ) A . F i l i p p o v ( D u b n a ) J . N i l s s o n ( G ö t e b o r g ) B . K u c h o w i t z ( W a r s a w ) J . P e t r a s ( B r a t i s l a v a )
B . P o n t e c o r v o ( D u b n a )
H . P r i m a k o f f ( P h i l a d e l p h i a ) G . T a v k h e 1 i d z e ( M o s c o w ) S . W e i n b e r g ( M . I . T . ) Y a .B .Z e l d o v i c ( M o s c o w )
G . M a r x ( B u d a p e s t ) A . F r e n k e l ( B u d a p e s t ) P . G n S d i g ( B u d a p e s t )
S e c r e t a r y
P r o c e e d i n g s S e c r e t a r y T e c h n i c a l S e c r e t a r y
* * * * * *
ÁSS ISTANTS
E . G a j z á g ó A . P a t k ó s L . G á l f i A . S e b e s t y é n J . P . H a r n a d C s . S ü k ö s d P . H a s e n f r a t z A . S . S z a l a y
C .S z e g ő
U / h c W G - d í L « ^ J t A v w | > 0 ^ kJ^At/o -k? “t£íí?. Qsvtqir S t o A ^ t o U > É o t L ^ e/j M*oJ(lu«i4o rfprlte
4 o
a t d ÍiLrae
*ÍJo C * í a i u v C É L ' " $ 2 .
O-^ "t^jí. ^yovkcfiMÁ o
M Í ü S b .
0 >fo ” í £ t
1 Wju? < a ív ö JÍ£ / V M ü f C L < - M i A J j Jt ~ $ i y j & ^ Q
^ n : a*^ v\
R e p o r t o n the B r o o k h a v e n S o l a r N e u t r i n o E x p e r i m e n t R.Davis Jr., J.C.Evans, V.Radeka and L.C.Rogers
A r e the s o l a r n e u t r i n o - e x p e r i m e n t s s u g g e s t i v e of the e x i s t e n c e of a r e s o n a n c e in the He^ + He^ s y s t e m ? / d i s c u s s i o n r ema rk /
V.N.Fetisov and Y.S.Kopysov S o l ar n e u t r i n o s : T h e o r y J . N .Bahcall
T h e b a c k g r o u n d e f f e c t s in s o l a r n e u t r i n o e x p e r i m e n t s R.Davis, A.W.Wolfendale and E.C.M.Young
T h e i n v e s t i g a t i o n of the b a c k g r o u n d in the s olar n e u t r i n o p r o p o r t i o n a l c o u n t e r s / d i s c u s s i o n remar k/
I .R .BarabanoV and A.A.Pomansky
N e w a p p r o a c h e s fto the s o l a r n e u t r i n o p u z z l e K.Lande, G .Bozoki, C.L.Lee and E .Fenyves D o u b l e b é t a d e c a y
E.Fiorini
N o t e o n U n i v e r s i t y of C a l i f o r n i a , I rvi n e d o u b l e - b e t a - d e c a y e x p e r i m e n t
M.Moe, D.Lowenthal and F.Reines L e p t o n c h a r g e c o n s e r v a t i o n G .Marx
N o t e on e l e c t r o n s t a b i l i t y and the P a u l i p r i n c i p l e / d i s c u s s i o n r e m a r k /
F.Reines and H.U.Sobel
R e m a r k o n s t a b i l i t y of vg / d i s c u s s i o n remark/
F.Reines
N e u t r i n o e x i t a t i o n of n u c l e a r le v e l s in 12C
H.Ubevall, B.A.Lamers, J .B .Langwovthy and F.J.Kelly A n t i n e u t r i n o - e l e c t r o n s c a t t e r i n g
H . S . G u r r , F.Reines and H.U.Sobel T h e L e p t o n é r a o f the Big Bang T . de Graaf
C o s m o l o g i c a l l i m i t o n n e u t r e t t o m a s s / d i s c u s s i o n r e m a rk / G.Marx and A.S.Ssalay
F i e l d - p a r t i c l e a s p e c t s of the c o s m o l o g i c a l n e u t r i n o p r o b l e m / d i s c u s s i o n r e m a r k /
B .Kuchowiaz
R e v i e w of the e x p e r i m e n t a l s i t u a t i o n on n e u t r a l c u r r e n t s C .Baltay
D i s c u s s i o n
5
23
29
77
85
87
99
121
123
135
137
139
.14 7
167 191
197 199 227
H .P i e t s c h m a n n
I n d u c e d t e n s o r i n t e r a c t i o n a n d s e c o n d - c l a s s c u r r e n t s B . E m a n a n d D . T a d i c
N u c l e a r b e t a - d e c a y e x p e r i m e n t s a nd s e c o n d - c l a s s w e a k c u r r e n t E. Vatai
T h e o r e t i c a l a p p r o a c h e s to Kl^ d e c a y N. Paver
T h e d e c a y K L -*■ 2\i /R e view/
A . D . U o l g o v , L . B . O k u n , V . I . Z a k h a r o V R e v i e w of the k£ > u+ + M p u z z l e R .J .O a k e s
M u o n p h y s i c s V. L . T e l e g d i
C o n c l u s i o n s of t h e first par t of the N e u t r i n o '72 E u r o p h y s i c s C o n f e r e n c e , B a l a t o n f ü r e d
B . P o n t e o o r v o
T . D . L e e 1
D i s c u s s i o n 25
P r e l i m i n a r y r e s u l t s o n the r a t i o of a n t i n e u t r i n o to n e u t r i n o t otál c r o s s - s e c t i o n s
A a a k e n , B u s s e l s , CERN, P a r i s (E .P .), M i l á n, O r s a y , L o n d o n (UCL)
C o l l a b o r a t i o n 29
H y p e r o n p r o d u c t i o n by a n t i n e u t r i n o s in G a r g a m e l l e
A a c h e n , B r u88e l s , C E R N , P a r i s (E .P .), M i l á n, O r s a y , L o n d o n (UCL)
C o l l a b o r a t i o n 39
N e u t r i n o p h y s i c s at Batavia: p r o s p e c t s and p r o g r e s s
B . C . B a r i s h 49
W h a t n e u t r i n o s c a n te l i us a b o u t p a r t o n s
R . P . F e y n m a n 75
D i s c u s s i o n 97
D e e p - i n e l a s t i c l e p t o n - n u c l e o n s c a t t e r i n g
J . K u t i 101
R e p o r t o n W b o s o n m o d e l of w e a k i n t e r a c t i o n s w i t h m a x i m a i C P v i o l a t i o n
R . E . M a r s h a k 129
V i r t u a l n e u t r i n o e f f e c t s
P. B u d i n i 149
C a l c u l a t i o n of s t a t i c Q u a n t i t i e s in W e i n b e r g ' s m o d e l
W. A . B a r d e e n , R .G a s t m a n s a n d B . L a n t r u p 163
A n a l y t i c r e n o r m a l i z a t i o n a nd e l e c t r o n - a n t i n e u t r i n o s c a t t e r i n g
Z . H o r v á t h a n d G . P & o s i k 175
A p p l i c a t i o n of t w i s t o r t h e o r y in w e a k i n t e r a c t i o n s / d i s c u s s i o n r e m ar k /
Z .P e r j é s 183
A t h e o r y o f u n i v e r s a l w e a k i n t e r a c t i o n s of l eptons
A . T . F i l i p p o v 185
C o s m i c r a y n e u t r i n o s
R . R e i n e s , H.H.Chen, H.S.Gurr, W.R.Kropp, P.B .L a nd eo ke r, J . F . L a t h o r p , U.G.Sandie, H.W.Sobel - M.F.Crouch - J .P .F .S e l l sa ho p, D.Bourne,
H . C o x e l l , D . K r a m e r , B . S . M e y e r ' 199
A n a n a l y s i s of c o s m i c ray m u o n n e u t r i n o e x p e r i m e n t s
J . L . O s b o r n e , A . W . W o l f e n d a l e a n d E . C . M . Y o u n g 223
2.Kunszt
P r o s p e c t s for the d e t e c t i o n of h i g h e r o r d e r w e a k p r o c e s s e s a n d the s t u d y of w e a k i n t e r a c t i o n s at h i g h e n e r g y
D .Cline
C o n c l u s i o n II V . F . Weisskopf
L I S T O F P A R T I C I P A N T S
SC A LIN G P R O P E R T IE S IN WEAK AND ELECTROM AG N ETIC P R O C E S S E S * T. D . L e e , C o l u m b i a U n i v e r s i t y , N e w Y o r k , N . Y .
In this talk, I shall first review the natúré of the scaling property that has been recently discovered in various high energy weak and electromagnetic processes, then examine its theoretical basis, and finally comment on its implications fór the future of high energy physics.
1. Scaling Hypothesis
The scaling property is the consequence of the scaling hypothesis which was first suggested^'by Bjorken and others. Here, we wish to state the scaling hypothesis in a form somewhat different from its original formulation, one that is perhaps more directly related to experimental results, and appears to be symmetric with respect to leptons and hadrons. Fór definiteness, we consider a purely leptonic or semi-leptonic reaction which can be either á second order electromagnetic process or a first order weak interaction process, e .g .,
+ - +
e + e - * | j + p ,
e+ + e -» hadrons , v + n -► u + hadrons, etc.
Furthermore, fór the semi-leptonic reaction we shall always sum over all final had
ronic channels. Let da be the appropriate differential cross section, which can be, in generál, written as
do = f (s, q2, m £ , mN ) X
a 2
0 )
G 2
— ---
T h i s r e s e a r c h w a s s u p p o r t e d i n p a r t b y t h e U . S . Á t o m i c E n e r g y C o m m i s s i o n
where the factors a 2 and G 2 are, respectively, the squares of the fine structure constant and of the Fermi constant, depending on whether the process is electromag
netic or weak,
s = (center-of-mass energy )2 ,
q2 represents the various relevant (4-momentum transfer)2 , m^ denotes the various lepton masses (m^ or m ) , and m^ denotes the various hadron masses (which can be either the nucleon mass itself, or the p and pion masses, e tc .).
The scaling hypothesis states that (i) if s and ] q 2 ] are much larger than then it is a good approximation to set m^ = 0 in the expression fór da and (ii) if s and | q2 J are much larger than , then it is a good approximation to set = 0 in the expression fór da , provided that all final hadronic channels are summed over. We emphasize that if one does nőt sum over different final hadron chan
nels, then there would obviously be cases in which one cannot neglect hadron masses.
Fór example, in e+e -* p° , the physical mass and the width of p° clearly cannot be neglected. One notes further that even in case (i) fór the leptons, though nőt ex- p licitly stated, it is understood that all different final channels of infrared photons are being summed over; otherwise dcr would be zero.
According to the scaling hypothesis, fór s and ] q2 ] larger than a few ( G e V ) 2 , one may set as a good approximation m ^ = m^ = 0 ; therefore, (1) becomes simply
cr2
da = f ( s , q2 ) X (2)
Aport from the couplíng constant a 2 or G 2 , the differential cross section d<j now depends only on s and the various q2 . These quantities represent (in the natural units "tí = c = 1) the only physical observables with the dimension (length)-2 . All the consequences of the scaling hypothesis can then be easily derived by a pure and simple dimensional analysis . The scaling hypothesis means simply the absence of any 2
baslc physical energy scale, such as m^ and . As we shall see, this enables us to connect various cross sections at a relatively low energy rangé to those at a much higher energy rangé.
2. Applications
(i) To illustrate the use of the scaling hypothesis, we shall first consider the föl—
lowing two electromagnetic processes, one purely leptonic and the other semi-leptonic:
■ + — .
e + e — p + y (3)
and
e + e -► hadrons. (4)
It follows from the scaling hypothesis that for
s = ( center-of-mass energy )2 » m 2
one may set m^ = m^ = 0 . The totál cross section for the purely leptonic reaction (3) depends then only on a 2 and s . From simple dimensional considerations, one sees that
a ( e +e -* p+p ) = constant • a 2/ s .
The constant can be evaluated by using quantum elecfrodynamics, which is consistent with the scaling hypothesis provided that radiative corrections are neglected; one finds then
, + - + - . 4 n a 2 a (e e - p p ) = --- .
3 s
Sim ilarly, according to the scaling hypothesis, if one sums over all final hadronic channels in the semi-leptonic reaction (4), for s > a few ( G e V ) 2 one may set = 0 . A simple dimensional analysis leads to
a (e +e -*■ hadrons) = constant • a 2/ s
where the constant may be determined by a relatively low energy experiment, which then enables one to predict the cross section in a much higher energy region. The pres-
.3 -1
ént col liding'beam results from Frascati are in agreement with the predicted s de- pendence.
(ii) Next, we consider the following weak processes;
± ± .
v + e -► v + e (5)
e e
and
v + N -* p + hadrons . (6)
H
Let q2 denote the (4-momentum transfer)2 between the incident neutrino and the target, and s be the (center-of-mass energy )2 , as before. For the purely leptonic reaction (5), if s and q2 are >> m j , on account of the scaling hypothesis, one may set m^ = 0 in the expression for da . Sim ilarly, for the semi-leptonic reaction
(6), if s and q2 are greater than a few ( G e V ) 2 , one may set m “ = 0 , r
provided all hadron channels are summed over. In either case, the differential cross section is proportional to G 2 and the proportionality factor depends only on q2 and s . Recalling that the dimension of G is (leng th)2 , one finds from simple dimensional considerations that the differential cross sections of both reactions must be of the form
dCT 2 - = G 2 - f ( ^ - ) r . 2 . t ,q2 (7) dq
where f is a dimensionless function depending only on the ratio (q 2/ s ) , which varies from 0 to 1 since s = q2 , the maximum value of q 2 . The correspond-
max n r
ing totál cross sections are of the form
a = constant • G 2 s . (8)
According to the usual (Current X Current) theory of the weak interaction, one can readily show that
da . - G 2
— „ (v e — v e ) = ----
d q 2 6 e ír
and
da / + +. G 2 , , q2 , T " <v e e dq e VG e ) = e T " < it sT " >
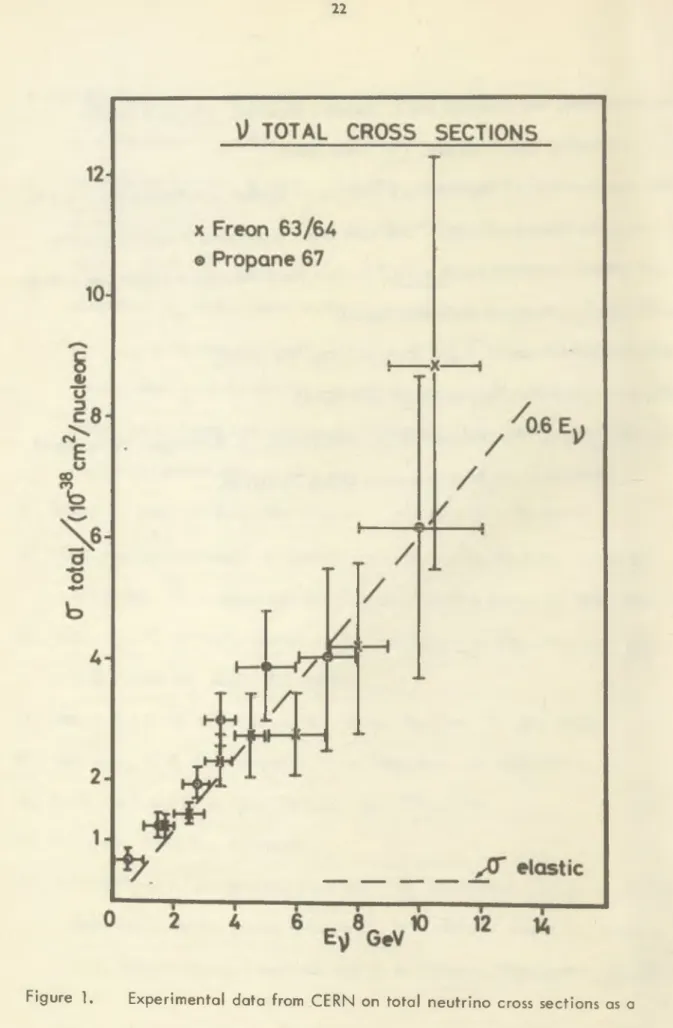
which agree with (7). In Figure 1, we reproduce the results from the CERN neutrino experiment , which gives, after averaging over N = p and n ,4
a (v + N — p + hadrons) = 0 .6 X 10"^ (cm2/nucleon) X f ( E ) in G e V l
H L v láb J
in good agreement with (B).
(iii) As a further example, one may consider the following two electromagnetic processes:
± ± ± ±
e + p — e + (a (9)
and
e * + p -*■ + hadrons (10)
in which one sums over all final hadron channels, as is done in the "deep" inelastic experiments of SLAC^.
In this problem, there are three independent invariant variables: s , q2 and p * q where s is the center-of-mass-energy squared, q is the virtual photon momentum, and p denotes either the 4-momentum of the initial proton £ in ( 1 0 ) J or that of the initial muon in (?)]]. It is customary to introduce a dimensioniess variable, called the scaling variable
u s - 2 p • q / q 2 . ' L
According to the scaling hypothesis, fór s and q2 greater than a few ( G e V ) 2 , one may set m^ = m^ = 0 ; therefore, the differential cross section depends only on q2 , s = q2 and u . From simple dimensional considerations, one deduces
n Tnax r
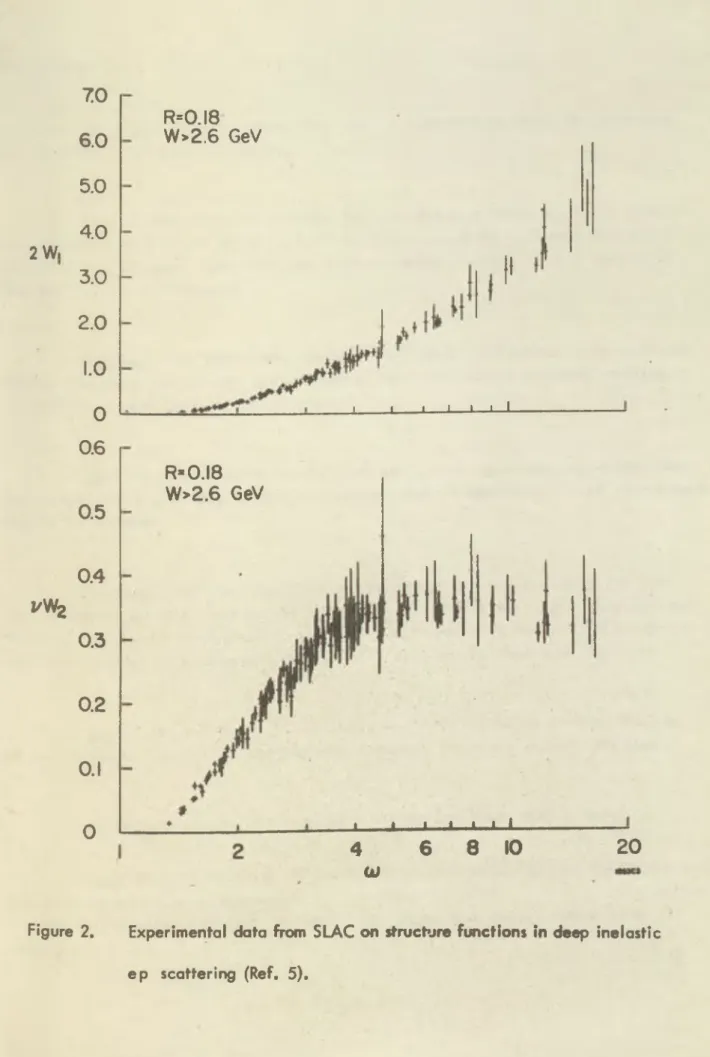
that fór the deep inelastic ep scattering
d2 a _ a 2 q2 . ....
77 F ( -7" / u ) • 0 D d q2 du (q 2 r s
Fór the purely leptonic reaction (9), because e p scattering is an elastic process, one has p2 = ( p + q ) 2 = - m 2 . Consequently, the scaling variable u
r
equals 1 and the corresponding function F is, therefore, proportional to 6 ( u - l ) . One may write, instead of (11),
d (7 j i i ± a r / Q \ j.
— (e H -* e H ) = --- f ( ) . (12)
d<t (q2)2 ‘
The dependence in both (11) and (12) can be exp licitly evaluated by using quantum electrodynamics, since it involves only lepton variables. One finds (fór m£ = mN = 0 )
( , V - e V > « = £ [ l - £ ♦ * < £ > ] 03)
do . ± ± 4ir
--- (e p - e p ) = —
d q ? ( q )
and d a 2
(e±p — e± + hadrons) = ° ["( - - — ) (vW 2) + ( — ) W , 1
d q 2 du <q*)2
L “ 5 ‘ 'J
(14)where W j and are cdl led structure functions; both are dimensionless and depend on u only. As shown in Figure 2, the validity of the scaling hypothesis has been ve ri-
5 fied by the recent SLA C data .
3. Theoretical Difficuities
While the statement of the scaling property is simple, it tums out to be rather difficult to find a solid theoretical basis of such a property for the hadrons.
This difficulty is connected with the so-called "mass singularities" of local fíeld theories^. In the case of quantum electrodynamics, such mass singularities are well known. They are connected with the high degeneracy between all states consisting of any number of pairs and photons moving along the same direction and with the same totál momentum. The approximation m^ = 0 can only be made in the first Born term; it leads to logarithmic divergences in higher order radiative corrections.
Experimentally, the mass singularity is supported by the fact that all zero-mass particles, such as the neutrino, the photon and the graviton, are found to be neutral.
Fortunately, in quantum electrodynamics, the coupling constant is small, and there
fore the zero mass approximation is a good one provided the energy v is nőt extra- ordinarily high, so that a In is « 1 . For the strong interaction of hadrons,
m £
the problem becomes more serious because of the large coupling constant associated with strong interactions. Let me briefly review various previous theoretical attempts and their difficuities:
(i) Parton model
While the original parton idea of Feynman^ has important heuristic values, it nevertheless puts a special emphasis on the infinite-momentum frame of reference.
It is suggested that Sn the infinite-momentum frame, the electromagnetic property of the assumed pointlike constituents of the physical nucleon can be treated as that of an assembly of independent free particles. The "infinite momentum frame", by itself,
is clearly nőt a Lorentz invariant concept. Furthermore, one can easily show^ that, in generál, the direction of the infinite momentum cannot be arbitrary. It must be limited to a certain restrictive set of directions, depending on the Virtual photon momentum; otherwise, the mass of each of the pointlike constituents has to be lighter than that of the physical proton, and that would be too unphysical. N aturally, this leads to questions of whether the parton model, especially of a spin i partiele such as the physical proton, can be derived from a relativistically invariant theory.
(íi) Perturbation theory
In the literature, there have been several attempts to try to dérivé the scaling property from the usual relativistic local field theory. So far, the only success has been limited to either the trivial case of free particles (free except for their electro-
3 magnetic interaction), or the unphysical case of a super-renormalizable <J> -type
a
theory in which all particles must be of zero spin. For the physically interesting case of spin 5 charged particles with somé non-electromagnetic interaction, straight- forward calculation in perturbative expansions leads to logarithmic deviations from scaling behavior .9
(iii) Perturbation theory with cut-offs
Efforts have been made to introduce a transverse momentum cu t-o ff^ to the perturbation theory. However, the transverse momentum cut-off in the field theo- retical derivation of scaling leads to a formalism and a scattering amplitude that are current-conserving only in the infinite momentum frame and in the scaling region.
Therefore, it is difficult to see how one may dérivé such an ad hoc cut-off procedure in a bona fide relativistic and gauge invariant field theory.
(iv) Light cone commutator
A straightforward application of field equations fór interacting spin i particles leads to a current commutator that is more singular than that fór free fields^ ^; there- fore, it does nőt seem to yield the desired scaling properties. Efforts have been made to introduce the so-called "formai manipulation" of current operators 12. However, at
present the theoretical foundation of such rules appears to be quite uncertain. In par- ticular, if one identifies such a "formai manipulation" with the usual Feynman regu
lator with a negative metric, then it is possible to show that while one may regularize the light-cone commutator, it is nőt possible to regularize the deep inelastic cross section unless such negative-metric particles are indeed produced asymptotically; fhis would violate unitarity and is certainly unrelated to the SLAC experiments.
Remarks:
We note that in both ép and v p type experiments the magnitudes of the deep inelastic cross sections are comparable to those of the corresponding purely lep
tonic ones. This strongly suggests that we may characterize the electromagnetic and weak interactions of hadrons, like those of the leptons, by somé local interactions.
On the other hand, as mentioned before, in a local field theory there is this difficulty of the "mass-singularity". Remembering that fór leptons, while the "mass-singularity"
becomes important in the infinite energy rangé, the approximation m^ = 0 remains a good one over quite an extensive intermediate energy rangé
m g < v < m exp ( a ^) .
Fór the hadrons, the theoretical difficulties discussed above are all associated with
parison with the similar situation fór leptons at least raises the question that perhaps fór hadrons one should alsó regard the scaling property to be valid nőt necessarily in the infinite energy limit, bút only in an intermediate energy rangé, one that includes all presently available machine energies. This view seems all the more reasonable, since at infinite energy and infinite 4-momentum transfer very likely the higher order electromagnetic and weak effects would become comparable in magnitude to the so- called strong interaction effects. In such a case, the observed deep inelastic cross sections are no longer simply related to the appropriate light-cone commutator. Ex- perimentally, the physical "scale" fór scaling is known to be only ~ 0 which is alsó of the same order of magnitude as the physical scale fór the elastic electromag
netic form factors of the nucleon. Thus, to explain the observed scaling phenomena it is certainly nőt necessary to require the relevant current commutator to have the desired behavior as an operator equation valid on the mathematical light cone. All that is needed is to construct theories in which the zero-mass approximation is a good one fór the mátrix element of the current commutator after it has been aVeraged over the physical nucleon state and at values of s and ] q2 | that are large bút need nőt be infinite.
As we shall see, it is indeed possible to develop such a bona fide local field theory, provided one regards the physical nucleon as a composite, nőt represented by a single elementary local field.
4. Bound-State Model
Next, 1 wish to discuss somé recent theoretical progress made in this direction; this work was done in collaboration with S. D. Drell. Our basic view
is to regard the physical proton p as a bound state of somé local fields. To i11us—
14 trate this bound-state concept, let me first discuss a simple model
The model that we shall discuss consists of only three fields: a spin £ charged field 1*(x) , a pseudoscalar neutral meson field ir(x) and a scalar neutral gluon field
<}>(x) . [T h e model can, of course, be easily extended to include charged meson fields. J The interaction Lagrangian density is assumed to be
13
where
£ + £ , (15)
K f ' '
£ = K ír2 * ,
K O T
and are unrenormalized coupling constants. Since £^ is a superrenormal- izable interaction and £j. is a renormalizable one7 the usual renormalization process can be easily carried out. The physical proton p is assumed to be a bound system
in the s^ state. Therefore, the field 4* is of opposite parity from p . In order fór p to be the lowest baryon state, the renormalized coupling constants f
l and k must satisfy
— ~ 0 (m ) 0 6 )
4 u ’
To describe the bound state, one can easily set up the Bethe-Salpeter equa- tion. In the ladder approximation (which w ill be removed in later discussions), the wave function <5 (k) is determined by
I ( k )
n
ír 4>where k is the relatíve momentum between <1* and ír , and V(q) is the covariant potential generated by the gluon field <J> . Since V(q) ~ 0 (“^ r ) at large momentum transfer q , one can easily establish that
£ (k) o ( r r ) as k2 oo
07)
In the simple model in which only I1 is charged, the standard minimál e le c tromagnetic interaction is
where denotes the electromagnetic field. In the "parton" language , one would then say that the charged constituent (or parton) 41 has a "point-like" e lec
tromagnetic structure. The evaluation of the electromagnetic form factors of the physical nucleon can be readily carried out. By using the diagram
one finds the familiar result that both F^(q2) and F^íq2) , being proportional _4
to the square of the wave function, decrease as q (apart from In q2 factors) at large q2 .
In this theory, the field represents the interpolating field of the continuum (p ír) . Because of parity conservation, 'P / p ; 1> is consequently nőt an interpo
lating field fór any single stable p artid é. Therefore, in any collision process 'P cannot appear in the asymptotic states. The following are two typical diagrams fór
e + p -*■ e + p + • • • ,
where the final hadron state " . . . 11 can consist of any number of mesons, ír or <j>
15
0)
Because of the convergence property of the wave function <£(k) , one derives the desired scaling property.
The ladder approximation is nőt necessary, since the inclusion of any crossed diagrams such as
etc.
leads only to additional convergent integrals. The asymptotic behavior of
^ (k) ~ r r 's therefore unaltered. A ll the above conclusions on the elastic form k^
factors and the deep-inelastic scaling property remain valid if we include (at least iteratively) all crossed diagrams in the description of the bound state p . The only diagrams that may lead to non-scaling results are diagrams in which hard mesons ( i . e . , mesons'with large transverse momentum) are emitted with a large probability, such as
To limit the probability of such hard meson emission we insist that
e =
4 tr should be small ,
(17)
say < 0 (10 ^) . This condition is certainly compatible with the coupling constant constraint (16) fór the bound-state description. The details of the model are given in Ref. 14. The following is a summary of the main features of this model:
1. Scaling holds (including all diagrams) for deep inelastic e p and en reactions, provided one neglects high order electromagnetic corrections and provided the labora- tory Virtual photon energy v , in units of G e V , is larger than 0(1) bút less than 0 ( e ^ £ ) . Since e is a free (though non-zero) parameter, one may approach the
light cone as nearly as possible by taking the limit e 0+ .
2. Because of (17), as e -* 0+ , there are only soft meson emissions; the transverse momentum distribution of the mesons is ~ k d2 k at large transverse momentum k .
-L J. ±
-1 3
3. As the scaling variable x - u -*■ 1 , both and vW^ approach ( 1 - x ) . This is rather encouraging, since it is in good agreement with the present experimental result, unlike most spin i parton models^ with an ad hoc transverse momentum cut-off which lead naturally to a linear ( 1 - x ) dependence as x -*• 1 .
/
4. As mentioned before, the elastic form factors are ~ 0 (q -4) at large q2 . In
this model, all masses are of the order of m or m ; this then "explains" why the
ír p
physical scale for deep inelastic scaling, as well as that for elastic form factors, are both of the order of 1 G e V .
The idea that p is the bound State of (^ ir) and <|> is the interpolating field of the (p ír) continuum differs from the bootstrap idea in a fundamental way. Here,
’l* is a local field; its interactions with the photon and with intermediate bosons (if they exist) must be of local character. If one wishes, one may alsó view this bound- state description as a Lorentz-invariant, gauge-invariant formulation of the parton model, in which the usual "point-like" assumption for the electromagnetic vertex of the constituent emerges simply as the standard minimál electromagnetic interaction
in a local field theory.
Assuming that the bound-state concept is correct, the theoretical basis of scaling can therefore be understood at least qualitatively. While m anyof the details remain to be worked out, fór most of the experimental applications, as we have discussed, all that is necessary is simply to use dimensional analysis, and that, after a little while, could become quite dull. Fortunately, there are good reasons to believe that the scaling hypothesis may nőt be an exact law of natúré in the ex- tremely high-energy limit. Besides the problem of mass singularities, mentioned earlier, we shall show that there must exist a new basic high energy scale, hitherto undiscovered. Since scaling means the absence of a basic physical energy scale, the presence of such a new basic energy scale therefore means the breakdown of scaling. It is well-known that at a center-of-mass energy higher than 300 G e V , the present Fermi theory of weak interactions would violate its unifarity limit. A new scale may alsó set in due to strong interactions, e . g . , if reál quarks do exist.
Fór the Fermi theory, a natural possibility is to regard the basic scale to be given by the Fermi constant itself,
i
G ~ 300 G e V .
On the other hand, if one assumes the weak interaction is governed by the same dimensionless constant a as that in the electromagnetic interaction, then the rele- vant scale can be much lower,
( a / G ) ^ ~ 30 G e V . 5 . Remarks
|^A more careful consideration may le a d ^ ' ^ to 37.3 G e V , or higher v a lu e s^ . J Throughout the study of microscopic physics, new frontiers are opened whenever a new basic energy scale is reached. We have the case of atomic and molecular physics with the electron-volt energy scale, nuclear physics with the MeV energy scale and the present strong-interaction physics with the G e V energy scale. In each case, at the energy scale of interest, we encounter a vastly rich structure of multiple energy levels and detailed dynamics; yet, when viewed against a much larger energy scale, this superstructure simply dissolves intő the continuum. The recent discovery of the scaling property strongly indicates that we are now again in a transition region: The familiar G e V scale is no longer significant, bút the still higher new high-energy scale is, as yet, unreached. While scaling is important, the future discovery of its violation should be of even greater significance.
References
1. J. D. Bjorken, Phys. Rév. 179, 1547 (1969). R. P. Feynman (unpublished);
Phys. Rév. Letters 23, 1415 (1969); in High Energy Colüsions, Conferenee held at the State University of New York, Stony Brook, 1969 (Gordon and Breach, New York, 1969). J . D. Bjorken and E. A . Paschos, Phys. Rév.
185, 1975 (1969).
2. See alsó V . A . Matveev, R. M. Muradyan and A . N . Tavkhelidze, JIN R E2-5962, Dubna, 1971. I wish to thank J. D. Bjorken fór calling my aíten- tion to this preprint, in which the authors have alsó independentiy emphasized the importance of dimensional analysis in high energy physics.
3. See the rapporteur's report given by S. D. Drell, in Proceedings of the Amsterdam International Conferenee on Elementary Particles (North-Holland Publishing Company, Amsterdam, 1972).
4. D. H. Perkins, Proceedings of the Topical Conferenee on Weok Interacrions, CERN (1969). See alsó various references mentioned in this review talk.
5. E. D. Bloom et a l., Proceedings of the Fifteenth Internationa! Conferenee on High Energy Physic^ K iev, LL S . S .R . (Atomizdat, Moseow, 1971).
Henry W. Kendall, Proceedings of the International Symposium on Electron and Photon Interactions (GomelI U h iv n ity Press, Ithaca, 1972). See alsó various references mentioned in these papers.
6. T. Kinoshita, J . Math. Phys. 3, 650 (1962). T. D. Lee and M. Nauenberg, Phys. Rév. 133, B1549 (1964).
7. Fór simplicity, let us assume that in the infinite momentum frame the 3-momentum k^ of the parton is parallel to the 3-momentum p of the physical proton; i . e . , in the frame p co , k = x p . Therefore. one may write fór the 4-momentum k^ = xp^ + 0 ( | p [ ^) . In the evaluation of the vW 2 function, in order to replace 8 ( q 2 + 2 k * q ) by 6 ( q 2 + 2 x p * q ) í one must have either the time component q of the virtual photon to remain finite as p-*- oo , or the differenc
o /».
kx - x p x to be zero identically £not just 0 ( | p | ^ • The former restricts the direction p of the infinite momentum frame, and the latter implies that the parton has no strong interaction and, furthermore, it is of mass xm^ where m^
denotes the proton mass.
8 . Sidney D. Drell and Tung-Mow Yan, Ann. of Physics 66, 578 (1971).
9. Y . S. Tsai (unpublished). R. Jackiw and G . Preparata, Phys. Rév. Letters 22, 975 (1969). S. L. Adler and W u-Ki Tung, Phys. Rév. Letters 22, 978 (1969).
10. See, e . g . , S. D. Drell, Donald J. Levy and Tung-Mow Yan, Phys. Rév. 187, 2159 (1969); DJ, 1035, 1617 (1970).
11. See, e . g . , J. M. Comwall and R. Jackiw , Phys. Rév. D4, 367 (1971).
12. See, e . g . , S. B. Treiman and D. Gross, Phys. Rév. D4, 1059 (1971).
13. S. D. Drell and T. D. Lee, Phys. Rév. D5, 1738 (1972).
14. T. D. Lee, Phys. Rév. (in press).
15. J. S. Ball and F. Zachariasen, Phys. Rév. 170, 1541 (1968). D. Amati, L. Can- eschi and R. Jengo, Nuovo Cimento 58, 783 (1968); D. Amati, R. Jengo, H. R. Rubinstein, G . Veneziano and M. A . Virasoro, Phys. Letters 27B, 38
(1968). M. Ciafaloni and P. Menotti, Phys. Rév. 173, 1575 (1968);
M. Ciafaloni, Phys. Rév. 176, 1898 (1968).
16. A linear ( 1 - x ) dependence is obtained by Bjorken and Paschos (loc. ci t . ) fór their three-quark model. The same linear dependence is alsó obtained by Drell, Levy and Yan (loc. c i t . ) in their field-theoretical calculation with an ad hoc transverse momentum cut-off.
17. J. Schechter and Y . Ueda, Phys. Rév. D2, 736 (1970).
18. T. D. Lee, Phys. Rév. Letters 26, 801 (1971).
19. S. Weinberg, Phys. Rév. Letters 19, 1264 (1967). J . Schwinger, University of Califom ia at Los Angeles preprint UCLA/7^/TEP/54.
Figure 1. Experimental data from CERN on totál neutrino cross sections as a function of laboratory neutrino energy (Ref. 4).
2 Wi
I/W2 6.0
5.0 4.0 3.0 2.0
1.0 0
0.6
0.5
0.4
0.3
0.2
0.1
0
70
R=0.I8 W>2.6 GeV
I'
■ ■ i --- 1— i— i— L
R-0.18 W>2.6 GeV
t_____i_____i— i— i— i—JL
4 6 8 10
GÜ
2 0
Figure 2. Experimental data from SLAC on structure functions in deep inelastic ep scattering (Ref. 5).
DlSCUSSION
K ö g e r l e r : In y o u r m o d e l y o u h a v e a d i m e n s i o n a l c o u p l i n g c o n s t a n t G. D o e s n ' t it d i s t u r b s c a l i n g ?
L e e : G d o e s h a v e d i m e n s i o n , b ú t the s c a l i n g a p p l i e s to th e r e ma i n - ing h a d r o n i c p a r t o nly. T h i s k i n d of a p p l i c a t i o n is of a p h e n o m e n o l o g i c a l nat úr é only. It m u s t b r e a k d o w n at h i g h e r en e r g y , n a m e l y at the e n e r g y of the s cale 1//G in d i s t a n c e .
F r e n k e l : C a n y o u r m o d e l a s s u r e tha t a f t e r the i n t e r a c t i o n w i t h the p h o t o n the p h y s i c a l p r o t o n d o e s n ' t b r e a k up intő p a r t i c l e s c o r r e s p o n d i n g to the fields w h i c h c o m p o s e the p r o t o n ?
Lee: In th i s t y p e of f i e l d t h e o r i e s it is n e c e s s a r y to a s su m e that the local f i e l d * belongs to the c o n t i n u u m , a n d no s t a b l e p a r t i e l e c o r r e s p o n d ing to it exists.
T e l e q d i : A r e y o u e x p e c t i n g a n e w e n e r g y rangé, and w h a t y o u are r ea l l y s a y i n g is t h a t s c a l i n g is w o n d e r f u l b ú t let's w a i t till it's b r o ke n ? T h a t is r e a l l y the n e x t s t e p in p h y s i c s O . K . ? B ú t if I u n d e r s t a n d c o r r e c t l y the I S R r e s u l t s at a t h o u s a n d G e V 2 c.m. e n e r g y still s h o w scaling.
Lee: I do n ő t t h i n k it is k n o w n w h a t r e a l l y h a p p e n s w i t h s c a li n g at the h i g h e s t ISR e n e r g y an d p e r h a p s s o m e b o d y w a n t s to c o m m e n t o n that.
T e l e g d i : I t h i n k the i n c l u s i v e r e a c t i o n s s h o w g o o d scaling.
Lee: Oh, the s c a l i n g in s t r o n g i n t e r a c t i o n s is r a t h e r d i f f e r e n t from the s c a l i n g as w e h a v e d i s c u s s e d in the e l e c t r o m a g n e t i c an d w e a k i n t e r a c t i o n s I think the a n a l y s i s is nőt the same; b ú t Dick, m a y be y o u w o u l d like to c o m m e n t ...
F e y n m a n t I d ö n t k n o w h o w to c o m m e n t b e c a u s e I d ö n t k n o w w h a t y o u h a v e a d d e d to the ide a t h a t m a n y p e o p l e h a v e to s e p a r a t e s t r o n g i n t e r a c t i o n f r o m w e a k i n t e r a c t i o n s . F ó r e x a m p l e in a l l o f the d i s c u s s i o n t h a t w e u s u a l l y m a k e o f thi s l e p t i c h a d r o n i n t e r a c t i o n w e s e p a r a t e t h e p i e c e t h a t ha s to do w i t h th e w e a k i n t e r a c t i o n f r o m t h e s t r o n g i n t e r a c t i o n . N o w l e t ' s s u p p o s e w e
c a n s t i l l d o that. T h e n the 37 G e V t h a t y o u w e r e t a l k i n g a b o u t m i g h t b e a f a i l u r e of s c a l i n g at the w e a k i n t e r a c t i o n end, and it c o u l d s t i l l be t h a t th e s t r o n g i n t e r a c t i o n sy s t e m , if it c o u l d b e s e p a r a t e d , w o u l d s c a l e a d i n f i n i t u m a n d t h a t the d i f f i c u l t y is o n l y in the w e a k i n t e r a c t i o n s o r the e l e c t r o d y n a m i c s . So I'd l i k e to as k w h e t h e r y o u feel t h a t the w e a k i n t e r a c ti o n s c a l i n g f a i l u r e i m p l i e s a f a i l u r e of the s c a l i n g of s t r o n g i n t e r a c t i o n ?
Lee: I t h i n k it p r o b a b l y d o e s i m p l y a failur e . N ő t i m m e d i a t e l y , b ú t in the d i s t a n t f u t u r e s u c h a f a i l u r e is a l m o s t i n e v i t a b l e b e c a u s e t h e s e p a r a - ti o n b e t w e e n the w e a k , e l e c t r o m a g n e t i c a n d s t r o n g i n t e r a c t i o n s is o n l y o f a t e m p o r a r y n a t ú r é . L e t us c o n s i d e r r e a c t i o n s w h e r e al l q 's a r e v e r y, v e r y 2 l a r g e .T h e o r e t i c a l l y the s e p a r a t i o n w o u l d b e d i f f i c u l t b e c a u s e it c a n be m a d e o n l y a f t e r o n e is a b l e to c a l c u l a t e e v e r y t h i n g . E x p e r i m e n t a l l y it w o u l d b e d i f f i c u l t b e c a u s e h a d r o n s p r o d u c e d w i t h v e r y l a r g e t r a n s v e r s e m o m e n t a m a y be du e to s t r o n g o r e l e c t r o m a g n e t i c i n t e r a c t i o n s o r to a m i x t u r e of the two.
T h u s I t h i n k a 30 G e V c.m.s . e n e r g y w e m a y s t i l l s e p a r a t e t h e s e i n t e r a c t i o n s , b ú t a t 30 0 G e V it w o u l d b e m u c h ha r d e r .
M a r s h a k : R o u g h c a l c u l a t i o n s d u e to s e v e r a l g r o u p s h a v e i n d i c a t e d t h a t a c r i t i c a l l e n g t h in the w e a k i n t e r a c t i o n m a y c o r r e s p o n d to 10 G e V r a t h e r t h a n to 37 GeV. If it t u r n é d o u t tha t the m a s s of th e W b o s o n w e r e d o w n a r o u n d ÍO G e V w o u l d t h i s a l t é r y o u r s t a t e m e n t ?
L e e ; No, I t h i n k I w o u l d b e d e l i g h t e d . I t h i n k m o s t p h y s i c i s t s w o u l d b e v e r y h a p p y a n d c e r t a i n l y the g o v e r m e n t s w o u l d b e e v e n h a p p i e r .
M o f f á t ; Is t h e r e a p o s s i b i l i t y to e s t a b l i s h the c r i t i c a l l e n g t h j us t w o r k i n g w i t h t h e w e a k i n t e r a c t i o n s ?
Lee: T h i s o f c o u r s e d e p e n d s o n w h e n d o e s the w e a k i n t e r a c t i o n l en g t h c o m e in. If it c o m e s in a r o u n d 300 GeV, t h e n the s e p a r a t i o n is n e a r l y im- p o s s i b l e b e c a u s e it r e a c h e s the u n i t a r i t y limit. If it sets in at 37 G e V
t h e n it p r o b a b l y m a y be c a r r i e d out; this w i l l be just li k e w i t h th e e l e c t r o m a g n e t i c i n t e r a c t i o n . If it c o m e s in at y o u r 10 G e V t h e n I t h i n k the w e a k i n t e r a c t i o n is a v e r y d i f f e r e n t e n t ity.
B e l l : I w o u l d lik e to c l a r i f y the role p l a y e d b y t h e b o u n d s t a t e of t he p r o t o n . If y o u w e r e to w o r k o u t d e e p i n e l a s t i c s c a t t e r i n g o n y o u r p i o n w o u l d it s h o w a s c a l i n g r é g i m é ?
L e e ; T h e a n s w e r is yes. W h i l e t h e p h y s i c a l p r o t o n m u s t be a b o u n d s t a t e b e c a u s e it h a s s p i n 1/2, the p h y s i c a l p i o n m a y b e d e s c r i b e d e i t h e r b y a c a n o n i c a l f i e l d as in t h e m o d e l d i s c u s s e d here, or as a b o u n d state, b ú t in the l a t t e r c a s e y o u h a v e to re d o th e w h o l e g a m e one s t e p further.
B e l l : D o e s the D r e l l - L e v y - Y a n m o d e l , w h e r e the p r o t o n is n ő t a b o u n d state, s h o w a s c a l i n g r é g i m é ?
L e e ; No. If y o u a s s u m e t h a t t h e r e is a s i n g l e l o c a l f i e l d fór the p h y s i c a l p r o t o n , y o u w i l l r u n i n t ő d i f f i c u l t i e s . T h e e l e c t r o m a g n e t i c f o r m f a c t o r w i l l n ő t go d o w n li k e q -4 . S c a l i n g w i l l nőt b e true. C o n v e r s e l y , the q -4 b e h a v i o r of the f o r m f a c t o r is a s t r o n g a r g u m e n t fór a c o m p o u n d p r o t o n , as Z a c h a r i a s e n a n d A m a t i s t a t e d b e f o r e , and the s c a l i n g in d e e p - i n e l a s t i c s c a t t e r i n g i n d i c a t e s a g a i n t h a t t h e p r o t o n c a n n o t be d e s c r i b e d b y a s i n g l e c a n o n i c a l field.
R a d i c a t i ; T w o of the r e m a r k a b l e f e a t u r e s of the q u a r k m o d e l ar e t hat the t h r e e q u a r k s p r e d i c t the b a r y o n s p e c t r u m so w e l l and th a t t h e y h a v e n ' t b e e n seen. N o w h o w d o e s y o u r p r o t o n fit i n t ő S U/3/ b e c a u s e it c o n s i s t s of a
ij; an d a it ?
L e e : T h e i n t r o d u c t i o n of S U/3/ int ő the m o d e l p r e s e n t s no d i f f i c u l t y . T his, h o w e v e r , d o e s n ő t n e c e s s a r i l y i m p l y the e x i s t e n c e of q u a r k s . T h e p r e s e n t e v i d e n c e o n the m a s s s p e c t r u m , d u e to G e l l - M a n n , is of c o u r s e a v e r y s t r o n g a r g u m e n t f ó r t h e v a l i d i t y of SU /3 /. T h e e x p e r i m e n t a l e v i d e n c e on s u m rules a l s ó s u p p o r t s th e v a l i d i t y of SU/ 3/ , b ú t o n l y i n d i r e c t l y do e s it s u g g e s t the p o s s i b l e e x i s t e n c e o f t h e q u a r k s , s i n c e t h e s e are c o n n e c t e d o n l y w i t h low- - e n e r g y p h e n o m e n a of the o r d e r o f a f e w GeV. To p r o v e the e x i s t e n c e of q u a r k s w e h a v e to c r e a t e them, a nd w e h a v e to go to v e r y h i g h e n e r g i e s .
F l l i p p o v : I h a v e t w o r e m a r k s . T h e f i r s t o n e is t h a t in n o n r e n o r - m a l i z a b l e m o d e l s /e.g. in a m o d e l w i t h the e x c h a n g e o f p - m e s o n s / a p o w e r l i k e a s y m p t o t i c b e h a v i o u r f ó r f o r m a c t o r s is p o s s i b l e . T h i s w a s s h o w n som é time b y a g o B . A r b u z o v a n d m y s e l f fór t h e m o d e l in w h i c h p - m e s o n w a s c o n s i d e r e d as
" b o u n d st a t e " o f u - m e s o n s . T h e c r u c i a l p o i n t is v a n i s h i n g o f the b o u n d s t a t e w a v e f u n c t i o n at the o r i g i n a n d t h i s is q u i t e p o s s i b l e fór n o n r e n o r m a l i z a b l e i n t e r a c t i o n as wedl as fór r e n o r m a l i z a b l e one. T h e s e c o n d r e m a r k is t h a t the a p p l i c a t i o n s of the d i m e n s i o n a l a n a l y s i s m e n t i o n e d b y p r o f e s s o r L e e w e r e i n v e s t i g a t e d in d e t a i l s by the D u b n a g r o u p a n d r e v i e w e d in the p a p e r by M a t v e e v , M u r a d i a n a n d T a v k h e l i d z e . /JINR p r e p r i n t E 2 - 6 0 3 6 , D u b n a 1971/
PRELIMINARY RESULTS ON THE RATIO OF ANTINEUTRINO TO NEUTRINO TOTÁL CORSS-SECTIONS
Aachen, Brussels, CERN, Paris (E.P.), Milán, Orsay, London (UCL) C o l l a b o r a t i o n (presented by B. Degrange, L P N H E , Ecole Polyt e c h n i q u e P a r i s ) .
We present here the very preliminary results of the CERN 1971 ne u t r i n o experiment, using the large heavy.liquid bubble c h amber "Gargamelle", exposed to the CE R N n eutrino beam.
500 OOO photographs, equally d i vided among n e utrino and
an t i n eutrino exposures, are bei n g aríalyzed in the laboratories
at Aachen, Brussels, CERN, Paris (E.P.), Milán, Orsay and Lond o n (ÜCL
I.- E X P E R I M E N T A L CONDI T I O N S a) Rate of v and v events
Ta b l e 1 and table 2 show the compa r i s o n b e tween the present experi m e n t and the previous v and v experiments using the <1.2 m heavy liquid bubble chamber at CERN (1). One can see that the totál statistics e x pected in the 1.971 runs will be about 10 times the previous available statistics of v events,
and 30 times the p r evious statistics of v events. This is due, first of all, to the large v i sible volu m e of "Gargamelle" (about 7 m 3 ) , w h i c h we have however restri c t e d to a fiducial volu m e of 3.14 m 3 fór n eutrino interaction vertices, in order to avoid m e a s u r e m e n t problems.
The rema i n i n g factor in the increase of the statistics is d u e to a h i gher intensity of the CE R N proton s y n c h rotron and
to improvements in the ne u t r i n o beam.
The p r e l i m i n a r y results p r e s e n t e d here are based on the analysis of 90% of the a n t i n e u t r i n o film and o n l y 3% of the neutri no film.
b) T h e neutrino b e a m
The neu t r i n o and a n t i n e u t r i n o ener g y spectra allow c r o s s - s e c t i o n m e a s u r e m e n t s b e t w e e n 1 G e V and a b out 8 GeV. Under
1 GeV, the n eutrino flux is bad l y kno w n d u e to large u n c e r t a i n t i e * in the raeson p r o d u c t i o n spe c t r u m t neut r i n o s from pi o n decays
c o n t r i b u t e e s s e n tially under 5 GeV, w h e r e a s neut r i n o s from kaon deca y s contr i b u t e at! higher energies.
Th e ne u t r i n o (or antineutrino) flux is c a l c u l a t e d by fitting the m e a s u r e d m u o n flux in the shie l d i n g to the results of a M o nté C a r l o p r o g r a m u s i n g as input the p r o d u c t i o n spectra of pions and kaons m e a s u r e d e x p e r i m e n t a l ly at the p r o t o n energy of 24 GeV, and e x t r a p u l a t e d at GeV, and the cu r r e n t s in the
focusing horns.
Our present r e sult o n l y c oncerns the rat i o of a n t i neu t r i n o to n e u t r i n o cross sections t the errors on the neu t r i n o and a n t i n e u t r i n o flux n o r m a l i z a t i o n s are thus minimized.
c) Facll i t i e s o f f e r e d by " G a r g a m e l l e " .
"Gargamelle" 1 is a c y l i n d r i c a l chamber, w i t h a length of 4.8 m and a d i a m e t e r of 2 m. T h e v i s i b l e v o l u m e of 7 m^ allows 'a good I d e n t ification of the muons, since pions have a high
p r o b a bility of i n t e r acting b e f o r e leaving the c h amber > (the pion interaction length, a b out 60 cm, has to b e c o m p a r e d to the a v erage p o t e n t i a l length of 1.5 m ) .
A n o t h e r a d v a n t a g e is the d e t e c t i o n of n e utral pions.
The y-rays from tt0 d e cays are mo s t of the time conv e r t e d intő electron pairs inside the v i s i b l e volume, d u e to the short radia- tion length of C F j B r (X0 - 11 cm). T h e loss in Y.-rays is thus small and has a n e g l i g i b l e e f f e c t w h e n one co m p a r e s the nergies
of missing Y-rays and the totál visible energy of the neutrínó or ántineutrino event.
Moreover, neutrons produced by a neutrínó or ántineutrino interaction are often d e tected by the observation of a neutral star in the visible volume.
II.- ANALYSIS OF EVENTS
a) Selectlon of v and v candidates
Event s haviing at least one muon candidate (i.e. having a track, leaving the chamber or d ecaying in the chamber, or a negative track stopping in the chamber) have been retained as neutrínó or ánt i n e u t r i n o candidates. They have been measured when the vert e x was located in the 3.14 m fiduCial volume. We have requested that the totál visible m o m e n t u m in the be a m direction, P x , be greater than 0.6 GeV/c in order to remove the interactions of incoming pions in the chamber sintulating a n eutrínó (or
ántineutrino) event. Candi d a t e s have been retained only if their totál v i sible energy was greater than 1 G e V since the flux is u n known at lower energies. Mor e o v e r this cut removes most of the b a c k g r o u n d of n e utron interactions.
T h e a ccuracy on the totál v i s i b l e energy is of the order of ÍO %, and p r a c t i c a l l y always better than 30 %.
b) A n alysls of a part of the neutrínó film
This pr e l i m i n a r y résult is bas e d on the analysls of 11000 photographs only whi c h leads to a sample of 214 events satisfying the cuts d e fined previously. This sample is p r a c t ically free of backg r o u n d of neutral stars and ánti n e u t r i n o events. Alt h o u g h the statistics are still poor, the results shown in figure 1 are compatible w i t h the c r o s s -section a(v) = (0.8 + 0.2) 10 c m xE„ ,,
G e V m pár nucleon obt a i n e d in the previous CERN bubble chamber e xperlments •
c) Analysis of the ant i n e u t r i n o film
Abo u t 90% of the a n t i n e u t r i n o film has b e e n scanned and measured.
A first c o r r e c t i o n has to be applied, since the scanning efficiency fór the anti n e u t r i n o elastic interactions (v + p -*• y + n)
is lower than the e f f i c i e n c y fór oth e r interactions, due to the special t o pology of these events, (one single m u o n ) , whi c h can easily remain unno t i c e d by the scanner.
A n other correc t i o n is related to the b a c K g r o u n d of neutrino events in the anti n e u t r i n o film w h ich is b i g g e r than the b a c k g r o u n d of a n t i n e u t r i n o events in the neu t r i n o film.
In order to e stimate the neu t r i n o c o n t a m i n a t i o n in events having b o t h a and a candidate, (called ambi g u o u s events) , w e have used the fact that ambiguous events in the n e u t r i n o film are pr a c t i c a l l y all actual ne u t r i n o events ; the p r o b a b i l i t y fór a n e u trino event to be ambi^bus can thus be testimated in s e veral energy regions } on the basis of these data from the n e u t r i n o film, and of the number of un a m b i g u o u s n e u t r i n o events in the a n t i n e u t r i n o
.film, w e find that the b a c k g r o u n d is of the ord e r of 2%. under 4 GeV, .and of the order of 10% at high e r energy.
III.- RESULTS
Figure 2 shoWs the v a lues found fór the rat i o R of a n t i neu t r i n o to n e utrino cross-sections in five e n ergy regions from 1 G e V ,to 6 G e V ; the loss of e l astic a n t i n e u t r i n o events at the scanning
stage has b e e n acco u n t e d fór . O n e can c o n c l u d e that this ratio is surely less than one.
V a r i o u s t h e o r etical m o dels ^ p r e d i c t v a lues of this r a t i o ( extending from 1/3 to 1, at least fór h i g h energies. Our resu l t is in contr a d i c t i o n w i t h the d i f f r a c t i v e mode l s w h i c h p r e d i c t the v a l u e R=li it is in a g reement w i t h the p a r t o n mod e l w h i c h pr e d i c t s 1 / 3 ^ R < 0. 8 9 i it is even c o m p a t i b l e w i t h the lower limit R » ^ .