Matematika 1.

(1)

Fritz Józsefné, Kónya Ilona,

Pataki Gergely és Tasnádi Tamás

MATEMATIKA 1.

GYAKORLATOK

2011.

Ismertető Szakmai vezető

Tartalomjegyzék Lektor

Pályázati támogatás Technikai szerkesztő

Gondozó Copyright

(2)

A „Matematika 1.” elektronikus oktatási segédanyag a Budapesti Műszaki és Gazda- ságtudományi Egyetem Villamosmérnöki és Informatika Karán a mérnök-informatikus szakos hallgatók „Analízis 1” tárgyához készült, de haszonnal forgathatják más szakok, karok vagy műszaki főiskolák, egyetemek hallgatói is, akik hasonló mélységben hasonló anyagot tanulnak matematikából.

Az anyag numerikus sorok, sorozatok elméletét, egyváltozós valós függvények határ- értékét, folytonosságát, differenciálását és integrálását tárgyalja. A definíciók, tételek, bizonyítások mellett kiemelt szerepet kapnak a példák, és a gyakran előforduló feladat- típusok megoldásai.

A mintegy 260 oldalas elméleti anyagot kiegészíti egy több, mint 100 oldalas példa- tár, amely többségében megoldott, tematizált gyakorlófeladatokat tartalmaz. A két pdf állomány kölcsönösen hivatkozik egymásra. Az eligazodást tartalomjegyzék, valamint az elméleti anyagban található tárgymutató segíti. A megértést színes ábrák könnyí- tik, az érdeklődő olvasó pedig a Thomas Calculus illetve a Calculusapplets kapcsolódó weboldalaira is ellátogathat külső hivatkozásokon keresztül. A háttérszínezéssel tagolt elméleti anyag fekete-fehér változata is rendelkezésre áll, amely nyomtatásra javasolt formátum.

Kulcsszavak: sor, sorozat, folytonosság, kalkulus, differenciálás, integrálás.

(3)

iii

Támogatás:

Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0028 számú, a „Természettudományos (matematika és fizika) képzés a műszaki és informatikai felsőoktatásban” című projekt keretében.

Készült:

A BME TTK Matematikai Intézet gondozásában.

Szakmai felelős vezető:

Ferenczi Miklós

Lektorálta:

Pröhle Péter

Az elektronikus kiadást előkészítette:

Fritz Ágnes, Kónya Ilona, Pataki Gergely, Tasnádi Tamás

Címlap grafikai terve:

Csépány Gergely László, Tóth Norbert

ISBN 978-963-279-445-7

Copyright: Fritz Ágnes (BME), Kónya Ilona (BME), Pataki Gergely (BME), Tasnádi Tamás (BME)

„A c terminusai: A szerző nevének feltüntetése mellett nem kereskedelmi céllal szabadon másolható, terjeszthető, megjeleníthető és előadható, de nem módosítható.”

c

Fritzné, Kónya, Pataki, Tasnádi tankonyvtar.ttk.bme.hu

(4)

(5)

Tartalomjegyzék

Tartalomjegyzék 1

1. Sorozatok 3

1.1. Speciális (végtelenhez tartó) sorozatok . . . 3

1.2. Nagyságrendek összehasonlítása (nⁿ,n!,2ⁿ,n^k, n,logn) . . . 7

1.3. Sorozatok határértéke. . . 8

1.4. Két nevezetes határérték (√ⁿ p−−−→^n→∞ 1, √ⁿ n−−−→^n→∞ 1) . . . 14

1.5. Rekurzíve megadott sorozatok . . . 17

1.6. (1 +x/n)^{n n}−−−→^→∞ e^x határértékkel kapcsolatos feladatok . . . 20

1.7. Limesz szuperior, limesz inferior . . . 25

1.8. Egy alkalmazás: a kör területe . . . 27

2. Sorok 29 2.1. Numerikus sorok . . . 29

2.2. Alternáló sorok, Leibniz sorok . . . 31

2.3. Majoráns kritérium, minoráns kritérium . . . 33

2.4. Abszolút konvergencia, feltételes konvergencia . . . 35

2.5. Hibaszámítás pozitív tagú sorokra . . . 37

3. Egyváltozós valós függvények határértéke, folytonossága 41 3.1. Függvény határértéke . . . 41

3.2. Szakadások típusai . . . 47

3.3. lim x→0 sinx x = 1 határértékkel kapcsolatos példák . . . 49

4. Egyváltozós valós függvények deriválása 53 4.1. Differenciálás a definícióval . . . 53

4.2. A deriválási szabályok gyakorlása . . . 55

4.3. A deriválási szabályok + definíció gyakorlása . . . 58

4.4. Elemi függvények . . . 61

4.5. L’Hospital szabály . . . 68

4.6. Függvényvizsgálat. . . 69

4.7. Abszolút szélsőérték . . . 76

4.8. Implicit megadású függvények deriválása . . . 78 1

(6)

4.9. Paraméteres megadású görbék . . . 80

5. Egyváltozós valós függvények integrálása 82 5.1. Határozatlan integrál . . . 82

5.2. Parciális integrálás . . . 87

5.3. Racionális törtfüggvények integrálása . . . 89

5.4. Határozott integrál . . . 92

5.5. Területszámítás . . . 94

5.6. Integrálfüggvény . . . 96

5.7. Integrálás helyettesítéssel . . . 100

5.8. Improprius integrál . . . 103

5.9. Integrálkritérium . . . 107

(7)

1. fejezet Sorozatok

App⇒

Elm→

1.1. Speciális (végtelenhez tartó) sorozatok

Elm→ Definíció: Az an valós számsorozat végtelenhez tart, jelben lim

n→∞an = +∞

(vagy más jelöléssel a_n −−−→ ∞^n→∞ , vagy csak a_n → ∞), ha

∀P > 0 (P ∈R) esetén ∃N(P)∈N, melyre a_n > P, ha n > N(P).

Definíció: lim

n→∞an =−∞ , ha

∀M < 0 (M ∈R) esetén∃N(M)∈N, melyre a_n < M, ha n > N(M).

(Lehet M > 0-val is definiálni, ekkor ... a_n<−M ...)

1. Feladat: a_n = 6n³+ 3→ ∞ , mert

6n³ + 3> P ⇐⇒ 6n³ > P −3 ⇐⇒ n > ³

rP −3 6 , tehát N(P)≥h

3

rP −3 6

i .

([x] az x egész részét jelöli, mely az x-nél nem nagyobb legnagyobb egész, pl.:

[−0.8] =−1, [1.95] = 1.)

3

(8)

2. Feladat: a_n = 6n³ + 3n→ ∞,

6n³ + 3n > P: most így nem megy. Helyette becslés:

6n³+ 3n≥6n³ > P n > ³ rP

6 N(P)≥

3

rP 6

. (Az alsó becslésnél a 6n³ helyett állhatnan³, 3n, n, stb.)

3. Feladat: a_n =√

n²−n , lima_n =?

n²−n „határozatlan”, ∞ − ∞ alakú, de az a_n = p

n(n−1) alakból már látszik, hogy a_n→ ∞.

Az N(P) küszöbindex meghatározása:

Az √

n²−n > P egyenlőtlenséget nehézkes egzaktul megoldani. Inkább valamilyen becslést alkalmazunk. Természetesen több lehetőség van, például:

√

n²−n=p

n(n−1)>p

(n−1)(n−1) =n−1> P n > P + 1 Ennek megfelelően: N(P)≥[P + 1].

Vagy:

√

n² −n >

r

n²− n²

2 = n

√2 > P n > √

2P.

Ez a becslés akkor igaz, ha n²

2 > n , azaz ha n >2, tehát a küszöbindex:

N(P)≥max 2, [√

2P] .

4. Feladat: a_n =n³−3n²+ 5n+ 9→ ∞ , mert:

n³ −3n²+ 5n+ 9 > n³−3n² > n^∗ ³−n³ 2 = n³

2 > P n >√³ 2P A ∗ becslés akkor igaz, ha n³

2 > 3n², azaz ha n > 6, így N(P)≥max

[√³

2P], 6

(9)

1.1. SPECIÁLIS (VÉGTELENHEZ TARTÓ) SOROZATOK 5

5. Feladat: a_n = n³+ 3n

n²+ 2 → ∞, , mert:

n³+ 3n

n²+ 2 ≥ n³

n²+ 2n² = n

3 > P n >3P N(P)≥

3P

.

6. Feladat: a_n =−n²+ 3√

n−9→ −∞ , mert: +++

−n²+ 3√

n−9 < M(< 0) ⇐⇒ n²−3√

n+ 9 > −M (> 0) Az egzakt megoldás helyett most is érdemesebb először becsülni:

n²−3√

n+ 9 > n²−3√

n > n^∗ ² −n² 2 = n²

2 > −M

A ∗ becslés akkor igaz, ha n²

2 > 3√

n , ami egy bizonyos N₁ küszöbindex esetén az n > N1 indexekre teljesül. (Nem kell N1-et meghatározni, elég látni, hogy létezik.) Tehát N(P) ≥ max

N₁,[√

−2M] .

7. Feladat:

Gyakorló feladatok:

A megfelelő definícióval mutassa meg, hogy az alábbi sorozatok ∞-hez vagy −∞-hez tartanak!

a) a_n= 7n⁵+ 5 , b_n = 7n⁵−5 b) a_n= 7n⁵+ 5n² , b_n= 7n⁵−5n²

c) a_n=√

2n⁵−3n²

c

(10)

d) a_n=n⁴−2n³+ 6n²+ 3 e) an=−n³+ 50n²

Tétel: Ha lim

n→∞a_n =∞, és b_n ≥a_n, akkor lim

n→∞b_n=∞.

Megjegyzés: Elegendő, hogy b_n ≥a_n csak n > N₀ indexekre teljesül.

Tétel: a_n −−−→ −∞^n→∞

⇐⇒

b_n =−a_n −−−→ ∞^n→∞

. A tételeket nem bizonyítjuk.

8. Feladat:

A fenti tételek alkalmazásával mutassuk meg, hogy a következő sorozatok

∞-hez vagy −∞-hez tartanak!

a) a_n=n⁵−7n²+ 5n+ 3 (a_n > n⁵−7n² ≥n⁵−n⁵

2 = n⁵

2 → ∞)

b) a_n=√

n⁵+ 2n², illetve √

n⁵−2n²

c) a_n=√

n⁴+ 2n³−√

n⁴−5n³ (n ≥5) (a_n = n⁴+ 2n³−(n⁴−5n³)

√n⁴+ 2n³ +√

n⁴−5n³ = n² n²

7n r

1 + 2 n +

r 1− 5

n

≥

≥ 7n

√1 + 2 +√

1 + 0 = const.·n→ ∞)

d) a_n=√

n⁶−n⁴−√

n⁶ + 2n⁴

(11)

1.2. NAGYSÁGRENDEK ÖSSZEHASONLÍTÁSA (nⁿ,n!,2ⁿ,n^k,n,logn) 7

(Legyen b_n =−a_n. Megmutatjuk, hogy b_n→ ∞, (ez könnyebb), ebből már követke- zik, hogy an→ −∞.)

9. Feladat: a_n =√³

n⁶+n⁵−√³

n⁶−n⁵ → ∞ +++

a_n= α³−β³

α²+αβ+β² , ahol α=√³

n⁶+n⁵, β =√³

n⁶−n⁵.

1.2. Nagyságrendek összehasonlítása (n

ⁿ

, n!, 2

ⁿ

, n

^k

, n, log n)

Elm→

A ∞

∞ határozatlan alak, konkrét esetekben különböző határértékeket kaphatunk, pél- dául

n

n² →0, n³

n → ∞, 3n 5n → 3

5. Tétel:

a) nⁿ

n! → ∞; b) n!

2ⁿ → ∞; c) 2ⁿ

n → ∞; d) n

log₂n → ∞.

Bizonyítás:

a)

nⁿ

n! = n·n·. . .·n

1·2·. . .·n ≥n·1·1·. . .·1 =n → ∞ =⇒

| {z }

spec. rendőrelv

nⁿ

n! → ∞ b)

n!

2ⁿ = n(n−1)(n−2). . .2·1 2·2·. . .·2 ≥ n

2 ·1·1·. . .· 1 2 = n

4 → ∞ =⇒

| {z }

spec. rendőrelv

n!

2ⁿ → ∞ c) Legyen a_n= 2ⁿ

n . +++

c

(12)

Egyrészt a sorozat monoton nő, tehát a_n+1 ≥a_n, hiszen:

2ⁿ⁺¹ n+ 1

≥? 2ⁿ

n ⇐= 2n≥^? n+ 1 ⇐= n≥1 Másrészt a páros indexű részsorozat végtelenhez tart:

a_2n= 2²ⁿ

2n = 2ⁿ·2ⁿ

2·n = 2ⁿ⁻¹a_n ≥2ⁿ⁻¹a₁ = 2ⁿ→ ∞.

E két tulajdonságból következik, hogy a_n→ ∞.

d) Legyen a_n= n log₂n. +++

Belátható, hogy a sorozat monoton nő (ezt csak később tudjuk megmutatni), és a₂k →

∞. Ebből a két tulajdonságból következik az állítás.

A következőt kaptuk:

nⁿ n!2ⁿn^kn^k¹ logn, k ∈N⁺

Itt a „” jelet úgy kell olvasni hogy erősebb, vagy nagyobb nagyságrendű. Ezeket a fogalmakat a félév végén pontosítjuk.

Belátható, hogy an → ∞-ből következik, hogy 1

a_n → 0. Ennek alapján az előzőekből következik :

logn

n →0; n

2ⁿ →0; 2ⁿ

n! →0; n!

nⁿ →0

1.3. Sorozatok határértéke

Elm→

Szükséges ismeretek:

lima_n = A definíciója; példák N(ε) meghatározására; konvergens sorozat korlátos;

divergens sorozatok; műveletek konvergens számsorozatokkal.

•••

Néhány feladat az előadáson tanultakkal kapcsolatban:

(13)

1.3. SOROZATOK HATÁRÉRTÉKE 9

10. Feladat: a_n= 3n²+ 4n+ 7

n²+n+ 1 →3, N(ε) =?

|a_n−A|=

3n²+ 4n+ 7 n²+n+ 1 −3

= n+ 4

n²+n+ 1 ≤ n+ 4n n² = 5

n < ε, N(ε)≥

5 ε

Persze másképp is majorálhatunk. Ha egyszerűen megoldható, célszerű olyan becsléseket alkalmazni, melyek minden n-re jók.

11. Feladat: an= n²−10⁸

5n⁶+ 2n³−1, lim

n→∞an=?, N(ε) =?

a_n→0, mert a_n = n² n⁶

|{z}

= ¹

n4→0

1−¹⁰_n2⁸

5 + _n²3 −_n¹6

→ 0· 1−0

5 + 0−0 = 0

|a_n−A| =

n²−10⁸ 5n⁶+ 2n³−1

ha n ≥10⁴

= n²−10⁸ 5n⁶+ 2n³−1

| {z }

>0

< n² 5n⁶ < 1

n⁴ < ε

N(ε)≥max n

10⁴, 1

√4

ε o

12. Feladat: További gyakorló feladatok:

Írja le a lim

n→∞a_n = A ∈R definícióját és ennek alapján mutassa meg, hogy

a) lim

n→∞

2n³ −5n

n³ + 8 = 2 (N(ε) = ? ) b) lim

n→∞

4n³ + 3n+ 1

n³+ 7n+b = 4 ; b = 30, illetve b=−30 (N(ε) = ? )

c

(14)

c) lim

n→∞

10⁹−n³

4n⁵+ 3n³−6n = 0 (N(ε) = ? )

13. Feladat:

+++

an= 2n²+ 3n+ 6 3n² −1 → 2

3, N(ε) =?

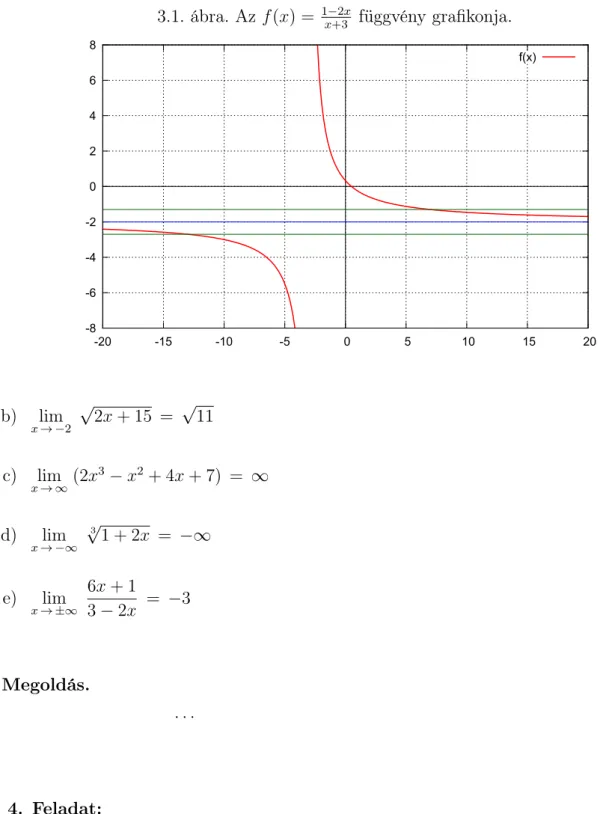
Megoldás. . . .

14. Feladat:

Vizsgálja konvergencia szempontjából az an = (n+ 1)!

(5−2n) n! sorozatot!

a_n = (n+ 1)!

(5−2n)n! = n+ 1 5−2n = n

n · 1 + ¹_n

5

n −2 → 1· 1 + 0

0−2 = −1 2

15. Feladat:

Vizsgálja konvergencia szempontjából az a_n =

n 2

n 3

sorozatot!

a_n =

n 2

n 3

=

n(n−1) 1·2 n(n−1)(n−2)

1·2·3

= 3

n−2 → 0

16. Feladat: a_n=√

2n²+ 5n−√

2n²−n →? Legyen α=√

2n²+ 5n, β =√

2n² −n. Ekkor:

a_n=α−β = (α−β) α+β

α+β = α² −β²

α+β = 6n

√2n²+ 5n+√

2n²−n =

= n

√n²

| {z }

=1

· 6

q

2 + _n⁵ +q 2−_n¹

→ 6

√2 +√

2 = 3

√2

(15)

17. Feladat: a_n =√

n⁴+ 2n²+ 3−√

n⁴+n →?

18. Feladat: an =√³

n³−3n+ 8−√³

n³+n+ 1 →? +++

Legyenα =√³

n³−3n+ 8, β =√³

n³+n+ 1. Ekkor:

a_n=α−β = α³−β³

α²+αβ +β² =. . .

Vizsgálja meg konvergencia szempontjából az alábbi sorozatokat!

a) a_n= 5−2n⁵

3n⁵+n⁴−2n²+ 3, b_n= 5−2n³

3n⁵+n⁴−2n² + 3, c_n= n⁶−7 3n⁵+n⁴−2n²+ 3 b) a_n = (3n+ 1)⁴

2n⁴+n²−3n+ 5 , b_n = (2n²+ 3)² (3n+ 5)⁴ c) a_n =

2n 4

n+1 2

n−1 2

d) a_n = √

9n²+ 7 − √

9n²+ 2n+ 5 e) a_n = √

4n⁴+n² −2 − 2n²

f) an = 1

n − √

n²+ 3n+ 5

20. Feladat:

+++

c

(16)

a_n=√

n²+ 2n+ 3−√

n²+bn+ 1

Határozzuk meg a b ∈R paraméter értékét úgy, hogy a sorozat határértéke a) ∞ vagy −∞,

b) véges, nem nulla szám, c) 0 legyen!

•••

Belátható, hogy

n→∞lim aⁿ =











0, ha|a|<1, 1, haa= 1,

∞, haa >1,

@, egyébként.

Sőt, általában igaz, hogy az exponenciális sorozat (aⁿ) gyorsabban nő, illetve csökken, mint bármely hatványsorozat (n^k, k∈N⁺), tehát például

n1 2

n n→∞

−−−→0, vagy n³−1 5

n n→∞

−−−→0.

Összefoglalva:

nlim→ ∞ n^kaⁿ =

(0, ha|a|<1, k ∈N⁺

∞, haa >1, k ∈N⁺

A fenti bekeretezett formulákat bizonyítás nélkül felhasználhatjuk a feladatok meg- oldásánál.

•••

Vizsgálja konvergencia szempontjából az alábbi sorozatokat!

21. Feladat: a_n = (−2)ⁿ + 3 5 + 7ⁿ =

−2 7

n 1 + 3 −1

2 n

5 1

7 n

+ 1

→ 0· 1 + 0 0 + 1 = 0

(17)

22. Feladat: a_n = (−3)ⁿ⁺¹ + 2²ⁿ⁺³

8 + 5ⁿ = −3·(−3)ⁿ + 8·4ⁿ

8 + 5ⁿ =

=

−3· −3

5 n

+ 8· 4

5 n

8· 1

5 n

+ 1

→ 0 + 0 0 + 1 = 0

23. Feladat:

a_n= (3)²ⁿ

(−3)ⁿ+ 10ⁿ →? b_n= (3)²ⁿ

3ⁿ+ 9ⁿ →? c_n = 9ⁿ

3ⁿ+ 2ⁿ →?

24. Feladat: an = n³ 2ⁿ+ 3ⁿ

2²ⁿ−3n² = n³ 2ⁿ+ 3ⁿ

4ⁿ−3n² = n³ ¹₂n

+ ³₄n

1−3n² ¹₄n → 0 (Felhasználtuk, hogy n^k aⁿ→0, ha |a|<1.)

25. Feladat: +++

A q ∈R paraméter függvényében határozzuk meg a következő sorozat határértékét:

a_n = 2²ⁿ

(−3)ⁿ+qⁿ →?

a) a_n = 5ⁿ⁺² + (−1)ⁿ 5ⁿ b) an = (−2)ⁿ − 3ⁿ

3ⁿ⁺¹ + 2²ⁿ c) a_n = 4ⁿ⁻¹ + n⁵ 3ⁿ⁺³

2²ⁿ⁺³ + 2ⁿ⁻³

c

(18)

d) a_n = 2ⁿ⁻¹ + n⁸ 4ⁿ 7 + 2³ⁿ⁺¹

1.4. Két nevezetes határérték ( √

ⁿ

p −−−→

^n→∞

1, √

ⁿ

n −−−→

^n→∞

1)

n→∞lim

√n

p= 1, p >0 lim

n→∞

√n

n = 1

27. Feladat: Keresse meg a következő sorozatok hatáérértékét!

a)a_n = ²ⁿ√

2n , b)b_n= √ⁿ

2n , c)c_n= ²ⁿ√ n Megoldás.

a) a_n → 1, mert az √ⁿ

n sorozat részsorozata.

b) b_n = √ⁿ

2n = √ⁿ 2 √ⁿ

n → 1·1 = 1

c) c_n = ²ⁿ r2n

2 =

2n√ 2n

2n√

2 → 1

1 = 1 ,mert a számláló és a nevező is két részsorozat.

Vagy egyszerűbben:

2n√ n =

q

√n

n → √ 1 = 1

28. Feladat: Vizsgálja meg konvergencia szempontjából a következő sorozatot!

a_n= √ⁿ n+ 1 Megoldás.

A rendőrelvvel dolgozunk:

√n

n

|{z}

↓ 1

≤ b_n = √ⁿ

n+ 1 ≤ √ⁿ

n+n = √ⁿ 2· √ⁿ

n

| {z }

↓ 1·1

=⇒ b_n → 1.

(19)

1.4. KÉT NEVEZETES HATÁRÉRTÉK (√ⁿ

p−−−−→^n→∞ 1, √ⁿ

n−−−−→^n→∞ 1) 15

Természetesen 1 < b_n alsó becslés is jó.

29. Feladat:

a_n = √ⁿ

2n³+ 3 b_n= ⁿ

s

2n²+ 3 4n²+n

Megoldás. Ezek a példák csak rendőrelvveloldhatók meg!!!! (Nem tudják megkerülni.)

√n

3

|{z}

↓ 1

≤ an = √ⁿ

2n³+ 3 ≤ √ⁿ

2n³+ 3n³ = √ⁿ 5· √ⁿ

n3

| {z }

↓ 1·1³ = 1

=⇒ a_n → 1.

n

r2 5

|{z}

↓ 1

= ⁿ s

2n²

4n²+n² ≤ b_n= ⁿ s

2n² + 3 4n²+n ≤ ⁿ

r2n²+ 3n² 4n² = ⁿ

r5 4

|{z}

↓ 1

=⇒ b_n → 1. Másik megoldás: b_n := √ⁿ

β_n Megmutatjuk, hogy β_n → 1

2 . . . Ezért

0.4 < βn < 0.6, ha n > N0 (∃N0) Ekkor √ⁿ

0.4

| {z }

↓ 1

< b_n = √ⁿ

β_n < √ⁿ 0.6

| {z }

↓ 1

, ha n > N₀

=⇒ b_n → 1 (Most is a rendőrelvethasználtuk fel.)

30. Feladat:

a_n= ⁿ√² n

c

(20)

Megoldás.

a_n = _n s

√n

n

|{z}→1

és √ⁿ

1 → 1 ÍGY NEM!!!!

Ez így "letakarás". Nem tanultunk olyan tételt, amely szerint így csinálhatnánk. Csak a sejtéshez használható a "letakarás".

Egy helyes megoldás:

√n

n → 1 =⇒ 0.9 < √ⁿ

n < 1.1, ha n > N₀ (∃N₀) Ekkor √ⁿ

0.9

| {z }

↓ 1

< a_n < √ⁿ 1.1

| {z }

↓ 1

=⇒ ⁿ√²

n → 1 (A rendőrelvethasználtuk fel.) Most lehet egy kicsit egyszerűbben is becsülni a rendőrelvhez:

1 ≤ ⁿ√²

n ≤ ⁿ√²

n² · · ·

a) a_n = √ⁿ

4ⁿ , b_n = √ⁿ

4ⁿ⁺² , c_n = ⁴ⁿ√

4, d_n= ⁵ⁿ√ 4n

b) a_n = √ⁿ

n⁵ 3ⁿ⁺²

c) a_n = √ⁿ

6n⁵+ 3n³−2n²+ 6

d) a_n = ³

r27n²+ 7n−3

8n²−5n+ 9 , b_n = ⁿ

r27n²+ 7n−3 8n²−5n+ 9

e) a_n= ⁿ

r5n²+ 3n+ 4 n³+ 7n²+ 6

(21)

1.5. REKURZÍVE MEGADOTT SOROZATOK 17

1.5. Rekurzíve megadott sorozatok

Elm→

Szükséges előismeret: Ha egy sorozat monoton és korlátos, akkor konvergens.

32. Feladat: Legyen

a₁ = 4, a_n+1 = 7− 10 an

rekurzíve adott sorozat!

(a_n) = (4, 4.5, 4.778, · · ·)

a) Mutassa meg, hogy 2≤a_n≤5 mindenn ∈N-re!

b) Indokolja meg, hogy (a_n) konvergens!

Határozza meg az (a_n) határértékét!

Megoldás.

a) Teljes indukcióval dolgozunk:

1) 2≤an≤5, ha n= 1,2,3 2) Tegyük fel, hogy 2≤a_n≤5 3) Igaz-e, hogy 2≤a_n+1 = 7− 10

a_n ≤5?

Az indukciós feltétel 0<2 ≤ a_n ≤ 5 miatt:

1 2 ≥ 1

a_n ≥ 1

5 | ·(−10) (A reciprokvételnél megfordultak a reláció jelek.)

−5 ≤ −10

a_n ≤ −2 |+ 7 2 ≤ 7− 10

an

=a_n+1 ≤ 5 Tehát igaz.

b) Sejtés: (a_n) monoton nő Bizonyítás:

I. módszer:

Bizonyítás: teljes indukcióval.

a) a₁ ≤a₂ ≤a₃ teljesül

c

(22)

b) Tfh. a_n−1 ≤a_n c) Igaz-e a_n ≤a_n+1 ?

Azaz a_n= 7− 10 an−1

≤? 7− 10

a_n =a_n+1 2. miatt 0<2≤an−1 ≤a_n. Innen

1

a_n−1 ≥ 1

a_n | ·(−10)

=⇒ − 10 an−1

≤ −10

a_n |+ 7

=⇒ a_n= 7− 10 an−1

≤ 7− 10

a_n =a_n+1 Tehát a számsorozat valóban monoton nő.

II. módszer:

a_n+1 = 7− 10 a_n

≥? a_n , (a_n>0) =⇒ a²_n−7a_n+ 10 = (a_n−2) (a_n−5) ≤^? 0 Mivel a)-ban beláttuk, hogy 2 ≤ a_n ≤ 5 , ezért az előző teljesül és így (a_n) monoton nő.

Megmutattuk, hogy a számsorozat monoton és korlátos

=⇒ (a_n) konvergens, és fennáll:

A= lim

n→∞a_n = lim

n→∞

7− 10 a_n

A= 7− 10

A =⇒ A= 5 vagy A = 2.

A = 2 nem lehet, mivel a_n ≥ a₁ = 4, ezért a_n nem esik a 2 szám pl. 1 sugarú környezetébe. Így A= lim

n→∞a_n = 5.

33. Feladat: Vizsgálja az alábbi sorozatok konvergenciáját!

a_n=p

2an−1 + 3

a) a1 = 1 : (an) = (1, 2.236, 2.73, · · ·) b) a₁ = 5 : (a_n) = (5, 3.605, 3.195, · · ·)

(23)

1.5. REKURZÍVE MEGADOTT SOROZATOK 19

Megoldás.

A =√

2A+ 3 =⇒ A²−2A−3 = 0 =⇒ A=−1 vagy A= 3.

Most csak A = 3 jöhet szóba, hiszen a_n > 0. Ha tehát a számsorozat konvergens, akkor A= 3. Ezért dolgozunk majd a korlátosságnál is a 3-mal. A megoldás vázlata:

a) Megmutatható teljes indukcióval, hogy (a_n) monoton nő és szintén teljes indukció- val, hogy a_n <3. Tehát a sorozat konvergens és az előzőek miatt A= 3.

(A Segédletben van hasonló példa kidolgozva.)

b) Most teljes indukcióval megmutatható, hogy (a_n) monoton csökken és a_n > 3 . Tehát a sorozat konvergens és az előzőek miatt A= 3 most is.

34. Feladat:

Gyakorló példák:

a)

a_n+1 = √

8a_n − 7 , n = 1,2,· · · és a₁ = 4 (an) = (4, 5, 5.74,· · ·)

a) Bizonyítsa be, hogy 1 < an < 7! b) Igazolja, hogy a sorozat monoton!

c) Konvergens-e ez a sorozat? Ha igen, mi a határértéke?

b)

a_n+1 = a²_n − 8

7 , n= 1,2,· · · és a₁ = 9 (a_n) = (9, 10.43, 14.4,· · ·)

a) Mely valós számok jöhetnek szóba a sorozat határértékeként?

b) Igazolja, hogy a_n > 8, n ∈N⁺ c) Igazolja, hogy a sorozat monoton!

d) Konvergens-e a sorozat!

c

(24)

c) Legyen

a₁ = 5, a_n+1= 8− 12 a_n

rekurzíve adott sorozat! (a_n) = (5, 5.6, 5.85, · · ·) a) Mutassa meg, hogy2≤a_n ≤6 mindenn ∈N-re!

b) Indokolja meg, hogy (a_n) konvergens! A felhasznált tételt írja le!

c) Határozza meg az (a_n) határértékét!

1.6. (1 + x/n)

^{n n}

−−−→

^→∞

e

^x

határértékkel kapcsolatos felada-

Elm

tok

→

nlim→ ∞

1 + x

n n

= e^x felhasználható.

Állapítsuk meg a következő sorozatok határértékét!

35. Feladat:

a_n =

1 + 1 6n²

6n²+2

Megoldás.

a_n =

1 + 1 6n²

6n² 1 + 1

6n² 2

→ e·1² = e (e_n részsorozatáról van szó.)

36. Feladat:

a_n =

n+ 5 n−4

n+3

Megoldás.

an =

1 + 5 n

n

1 + −4 n

n ·

1 + 5 n

3

1 + −4 n

3 → e⁵ e⁻⁴ ·1³

1³ = e⁹

(25)

1.6. (1 +x/n)^{n n}−−−−→^→∞ e^x HATÁRÉRTÉKKEL KAPCSOLATOS FELADATOK 21

Más átalakítással:

a_n =

n−4 + 9 n−4

n−4+7

=

1 + 9 n−4

n−4

·

1 + 9 n−4

7

→ e⁹·1⁷ = e⁹ Ez a fajta átalakítás bizonyos példáknál sokkal hosszabb, ezért az első módszert hasz- nálata javasolt, de persze ez nem kötelező.

37. Feladat:

a_n =

n²+ 2 n²+ 3

n²+7

Megoldás.

a_n =

n²+ 2 n²+ 3

n²

·

n²+ 2 n²+ 3

7

=

1 + 2 n²

n²

1 + 3

n² n² ·





 1 + 2

n² 1 + 3

n²







7

→ e²

e³ ·1⁷ = 1 e

Másik megoldás:

a_n =

(n²+ 3)−1 n²+ 3

(n²+3)+4

=

1 + −1 n²+ 3

n²+3

·

1 + −1 n² + 3

4

→ e⁻¹·1⁴ = 1 e

38. Feladat:

a_n =

3n+ 5 3n−4

3n

, b_n =

3n+ 5 3n−4

2n

Megoldás.

an =





 1 + 5

3n 1 + −4 3n







3n

→ e⁵

e⁻⁴ = e⁹

b_n =





 1 + 5

3n 1 + −4

3n







2n

=













1 + 5/3 n 1 + −4/3

n







n





2

→

e^5/3 e^−4/3

²

= e⁶

c

(26)

39. Feladat:

Gyakorló példák:

Keresse meg az alábbi sorozatok határértékét!

a) an =

1 + 1 n

5n

b) a_n =

1 + 1 5n

n

c) a_n =

1 + 1 5n

6n

d) a_n =

1 + 1 n

10!n

e) a_n =

5− 1 n

n

5 + 1

n n

f) a_n =

1 + 8 n

2n

g) a_n =

n+ 7 n+ 4

n+4

h) a_n =

n+ 7 n+ 3

n

i) a_n =

2n+ 7 2n+ 3

2n

j) a_n =

2n+ 7 2n+ 3

n

k) a_n =

2n+ 7 2n+ 3

2n+5

40. Feladat:

Gyakorló példák:

A paraméterek megadott értékeire keresse meg az alábbi sorozat határértékét!

a_n =

3n³ + 5 3n³ + 3

α n³+β

a) α= 3, β = 0 b) α= 3, β = 2

c) α= 1, β = 0 d) α= 6, β = 0

41. Feladat:

an =

1 + 1 n²

n

(27)

1.6. (1 +x/n)^{n n}−−−−→^→∞ e^x HATÁRÉRTÉKKEL KAPCSOLATOS FELADATOK 23

Megoldás.

ÍGY TILOS! : an = ⁿ s

1 + 1

n² n²

→ √ⁿ

e → 1

Ez így "letakarás"! Ez a sejtéshez használható:

n

s

1 + 1 n²

n²

∼ √ⁿ

e → 1

De precízen meg kell mutatni. (Persze kimondható lenne használható tétel, de mi nem mondtunk ki ilyent.)

Helyesen:

pn

e−0,1

| {z }

↓ 1

< a_n =

n

v u u u u u u u t

1 + 1

n² n²

| {z }

↓ e

< pⁿ

e + 0,1

| {z }

↓ 1

, ha n > N₀

=⇒ a_n → 1 Persze más becslés is jó. Pl.: √ⁿ

2 ≤ a_n < √ⁿ

3 stb.

42. Feladat:

an =

1 + 1 n

n²

Megoldás.

a_n =

1 + 1 n

nn

≥ 2ⁿ → ∞ =⇒

spec. rendőrelva_n → ∞

43. Feladat: +++

a) a_n =

1− 1 n⁴

n³

b) b_n =

1− 1 n⁴

n⁵

Megoldás. · · ·

44. Feladat:

c

(28)

Gyakorló példák:

Keresse meg az alábbi sorozatok határértékét!

a) a_n =

1 + 2 n

n²

b) a_n =

1− 2 n

n²

c) an =

n² + 3 n² + 5

n³

45. Feladat:

a_n =

4n+ 1 4n+ 5

n

, b_n =

4n+ 1 7n+ 5

n

, c_n =

6n+ 1 4n+ 5

n

Megoldás.

a_n =

1 + 1/4 n

n

1 + 5/4 n

n → e^1/4 e^5/4 = 1

e

0 < bn =

4n+ 1 7n+ 5

n

<

4n+n 7n

n

= 5

7 n

| {z }

↓ 0

=⇒

rendőrelv bn → 0

c_n =

6n+ 1 4n+ 5

n

≥

n≥5

6n 4n+n

n

= 6

5 n

→ ∞ =⇒

spec. rendőrelvc_n → ∞ De lehet kiemeléssel is egyszerűbb alakra hozni. Pl.:

b_n =

4n+ 1 7n+ 5

n

= 4n

7n n

| {z }

=





4 7





n

·

1 + 1/4 n

n

1 + 5/7 n

n → 0·e^1/4 e^5/7 = 0

(29)

1.7. LIMESZ SZUPERIOR, LIMESZ INFERIOR 25

1.7. Limesz szuperior, limesz inferior

Elm→

46. Feladat:

a_n = 4−n²

n+ 3 lim supa_n = ?, lim infa_n = ?

47. Feladat:

a) a_n =

cosn π 2

2n²−3

n²+n+ 8 lim supa_n = ?, lim infa_n = ?, lim

n→ ∞ a_n = ? b) b_n =

cosnπ 2

2n²−3

n³+n+ 8 lim supb_n = ?, lim infb_n = ?, lim

n→ ∞ b_n = ? Megoldás.

a) α_n := 2n² −3 n²+n+ 8 =

2− 3 n² 1 + 1

n + 8 n²

→ 2

Ha n= 2k+ 1 : a_n = 0 → 0 Ha n= 4k : an = αn → 2 Ha n= 4k+ 2 : a_n = −α_n → −2

Tehát a torlódási pontok halmaza: S ={−2, 0, 2}

=⇒ lim supan = 2, lim infan = −2, lim

n→ ∞ an @ b) βn := 2n²−3

n³+n+ 8 . . . → 0 =⇒ lim supbn = lim infbn = lim

n→ ∞ bn = 0

48. Feladat:

c

(30)

lim supa_n = ?, lim infa_n = ?, lim

n→ ∞ a_n = ? a) a_n = (−3)ⁿ+ 8

5 + 2²ⁿ⁺¹ b) a_n = (−4)ⁿ+ 8

5 + 2²ⁿ⁺¹

Megoldás. . . .

49. Feladat:

an =

rn³+ (−1)ⁿn³

3n³+n+ 7 lim supan = ?, lim infan = ? Megoldás.

Ha n páros: a_n =

r 2n³

3n³+n+ 7 = v u u t

2 3 + 1

n² + 7 n³

→ r2

3 Ha n páratlan: a_n = 0 → 0

=⇒ lim supan = r2

3 , lim infan = 0

50. Feladat:

a_n =

r2n³+ (−1)ⁿn³

3n³+n+ 7 lim supa_n= ?, lim infa_n= ?

Megoldás. . . .

51. Feladat:

+++

a_n =

3−n 5 +n

n

4n−1 2n+ 5

3

lim supa_n= ?, lim infa_n= ?

Megoldás. . . .

(31)

1.8. EGY ALKALMAZÁS: A KÖR TERÜLETE 27

52. Feladat:

Gyakorló példák:

Határozza meg az alábbi sorozatok limeszét (ha létezik), valamint limesz szuperiorját és a limesz inferiorját!

a) a_n = 3 + 2²ⁿ

−4ⁿ+ 1 b) a_n = 3 + 2²ⁿ

(−4)ⁿ+ 1 c) a_n = (−4)ⁿ+ 3²ⁿ⁺¹

5 + 9ⁿ⁺¹ , b_n = a_n·cosnπ d) an = (−1)ⁿ

3n−3 3n+ 2

6n+2

e) a_n = 4ⁿ⁺¹+ (−2)ⁿ 2²ⁿ⁺¹+ 3ⁿ⁻¹

1.8. Egy alkalmazás: a kör területe

Elm→

nlim→ ∞

sin1 n 1 n

= lim

n→ ∞ n·sin1

n = 1 (Bizonyítás később.)

nlim→ ∞

sina an n

= lim

n→ ∞

n

a ·sina

n = 1, a ∈R (Bizonyítás később.)

53. Feladat:

nlim→ ∞ n·sin3 n = ?

Megoldás.

c

(32)

nlim→ ∞ n·sin3

n = lim

n→ ∞

sin 3 n 3 n

·3 = 1·3 = 3

54. Feladat:

Határozzuk meg az r sugarú kör területét mint a beírt szabályos n-szögek területeinek limeszét!

Megoldás.

A szabályos n-szög egy háromszögének területe: t_h =

r·r·sin2π n 2 Így a szabályos n-szög területe:

t_n = n·

r²·sin2π n

2 = r²·

sin2π n 2π

n

| {z }

↓ 1

·π → r²· π

(33)

2. fejezet Sorok

Elm→

2.1. Numerikus sorok

_App

⇒

1. Feladat:

Konvergens-e a

∞

X

k=1

√k+ 1 − √ k

sor? (A definícióval dolgozzon!)

Megoldás.

sn =

n

X

k=1

√

k+ 1 − √ k

= √

2 − √ 1

+ √

3 − √ 2

+ √

4 − √ 3

+ . . .

+ √

n − √ n−1

+ √

n+ 1 − √ n

= √

n+ 1−1 s = lim

n→ ∞ s_n = lim

n→ ∞(√

n+ 1−1) = ∞. Tehát a sor divergens.

Geometriai sor összege: ^Elm→

∞

X

n=0

a qⁿ =

∞

X

n=1

a qⁿ⁻¹ = a

1−q , ha |q|<1

29

(34)

2. Feladat:

∞

X

n=1

2²ⁿ

(−5)ⁿ⁺² = ? (Állapítsa meg a sor összegét!) Megoldás.

s =

∞

X

n=1

2²ⁿ (−5)ⁿ⁺² =

∞

X

n=1

1 25·

−4 5

n

= 1 25· −4

5

| {z }

a

+ 1 25·

−4 5

2

+ 1 25·

−4 5

3

+· · · =

=

−4 125 1− −4

5 Itt q = −4

5 , |q|<1, tehát a geometriai sor konvergens.

3. Feladat:

∞

X

n=1

2³ⁿ⁺¹ + (−5)ⁿ 3²ⁿ⁺² = ? Megoldás.

A sor két konvergens geometriai sor összege. Tanulni, sőt bizonyítani fogunk egy tételt,

Elm→

mely szerint számolhatjuk tagonként a sorösszeget és az eredményeket összegezzük.

s =

∞

X

n=1

2³ⁿ⁺¹ + (−5)ⁿ 3²ⁿ⁺² =

∞

X

n=1

2 9 ·8ⁿ

9ⁿ +

∞

X

n=1

1

9· (−5)ⁿ

9ⁿ = s₁ + s₂ A konstans is kiemelhető:

s = 2 9·

∞

X

n=1

8 9

n

+ 1 9·

∞

X

n=1

−5 9

n

= 2 9·

8 9 1− 8

9 + 1

9 ·

−5 9 1− −5

9

4. Feladat:

∞

X

n=2

x²ⁿ

4ⁿ Milyen x-re konvergens és mi az összege?

(35)

2.2. ALTERNÁLÓ SOROK, LEIBNIZ SOROK 31

2.2. Alternáló sorok, Leibniz sorok

App⇒

Elm→ Emlékeztetünk arra, hogy a két fogalom nem ekvivalens! Minden Leibniz sor alternáló sor, de nem minden alternáló sor Leibniz sor.

Konvergensek-e az alábbi sorok?

5. Feladat:

a)

∞

X

n=1

(−1)ⁿ⁺¹ 1

√5

n+ 5 b)

∞

X

n=1

(−1)ⁿ⁺¹ 1

√n

n⁵+ 5 Megoldás.

a) c_n := 1

√5

n+ 5.

Mivel c_n & 0 (monoton csökkenően tart nullához), a sor Leibniz típusú és így konvergens.

b) Most c_n = 1

(√ⁿ

n)⁵+ 5 → 1

1 + 5 = 1 6 6= 0

=⇒ a sor divergens, mert nem teljesül a konvergencia szükséges feltétele, az álta- lános tag nem tart 0-hoz.

6. Feladat:

∞

X

n=1

(−1)ⁿ⁺¹

n+ 1 n+ 5

n

Megoldás.

c_n:=

n+ 1 n+ 5

n

=

1 + 1 n

n

1 + 5

n

n → e¹ e⁵ = 1

e⁴ 6= 0

Tehát az általános tag nem tart 0-hoz, így nem teljesül a konvergencia szükséges feltétele, ezért a sor divergens.

c

(36)

7. Feladat:

∞

X

n=1

(−1)ⁿ 5ⁿ 2ⁿ+ 10ⁿ Mutassa meg, hogy Leibniz sorról van szó!

Adjon becslést az s≈s99 közelítés hibájára!

Megoldás.

c_n = 5ⁿ 2ⁿ+ 10ⁿ =

1 2

n

1 5

n

+ 1

→ 0

0 + 1 = 0

Még meg kell mutatnunk, hogy a sorozat monoton csökkenő. (Ez most nem triviális, mert n növelésével a számláló és a nevező is nő.)

c_n+1 <^? c_n 5ⁿ⁺¹

2ⁿ⁺¹+ 10ⁿ⁺¹

<? 5ⁿ 2ⁿ+ 10ⁿ

5·(2ⁿ+ 10ⁿ) <^? 2·2ⁿ + 10·10ⁿ 3·2ⁿ <^? 5·10ⁿ

3 5

<? 5ⁿ

Ez pedig igaz minden n-re és ebből következik visszafelé, hogy c_n+1 < c_n, tehát a sorozat monoton csökkenő.

Ezzel bebizonyítottuk, hogy a sor Leibniz típusú, így konvergens.

Leibniz sorok esetén az s ≈s_n =

n

X

k=1

(−1)^k+1 c_k közelítés hibája:

|H| = |s−s_n| ≤ c_n+1

Ezért az s≈s₉₉ közelítés hibájáról az alábbit mondhatjuk:

|H| = |s−s₉₉| ≤ c₁₀₀ = 5¹⁰⁰ 2¹⁰⁰+ 10¹⁰⁰

8. Feladat:

∞

X

n=1

(−1)ⁿ 3ⁿ+ 5 7ⁿ+ 9ⁿ

(37)

2.3. MAJORÁNS KRITÉRIUM, MINORÁNS KRITÉRIUM 33

Mutassa meg, hogy Leibniz sorról van szó!

Adjon becslést az s≈s₉₉ közelítés hibájára!

Megoldás.

. . .

9. Feladat:

∞

X

n=1

(−1)ⁿ⁺¹ 1

√n

n⁴+ 5 Konvergens-e a sor?

Megoldás.

. . .

10. Feladat:

∞

X

1

(−1)ⁿ 2n²+ 5 n³ Konvergens-e a sor?

Megoldás.

. . .

2.3. Majoráns kritérium, minoráns kritérium

App⇒

Elm→ Csak olyan példa lehet most, amelyiknél geometriai sorral vagy

∞

X 1

n^α sorral lehet majorálni, minorálni.

c

(38)

Vizsgálja meg konvergencia szempontjából az alábbi sorokat!

11. Feladat:

∞

X

n=1

2n³−n+ 3 3n⁴+ 2n²+ 7

Megoldás.

Divergenciát várunk, mert . . .. Ezért a minoráns kritériumot használjuk:

a_n := 2n³−n+ 3

3n⁴+ 2n²+ 7 ≥ 2n³−n³+ 0

3n⁴+ 2n⁴+ 7n⁴ = 1 12· 1

n ; 1

12

∞

X

n=1

1

n divergens

=⇒

∞

X

n=1

a_n divergens.

12. Feladat:

∞

X

n=1

n²−n+ 3 2n⁵+ 2n²+ 7

Megoldás.

Konvergenciát várunk, mert . . .. Ezért a majoráns kritériumot használjuk:

a_n := n²−n+ 3

2n⁵+ 2n²+ 7 ≤ n²−0 + 3n²

2n⁵+ 0 + 0 = 2· 1

n³ ; 2

∞

X

n=1

1

n³ konvergens

=⇒

∞

X

n=1

a_n konvergens.

13. Feladat:

∞

X

n=1

2ⁿ+ 3ⁿ⁺² 1 + 6ⁿ⁻¹

Konvergencia esetén adjon becslést az s ≈ s100 közelítés hibájára!

Megoldás.

Konvergenciát várunk, mert . . .. Ezért a majoráns kritériumot használjuk:

(39)

2.4. ABSZOLÚT KONVERGENCIA, FELTÉTELES KONVERGENCIA 35

a_n := 2ⁿ+ 3ⁿ⁺²

1 + 6ⁿ⁻¹ = 2ⁿ+ 9·3ⁿ 1 + 1

6 ·6ⁿ

< 3ⁿ+ 9·3ⁿ 1 6·6ⁿ

= 60· 1

2 n

60·

∞

X

n=1

1 2

n

konvergens geometriai sor (0< q = 1

2 <1) =⇒

∞

X

n=1

a_n konvergens.

Hibabecslés:

s ≈

100

X

n=1

2ⁿ+ 3ⁿ⁺² 1 + 6ⁿ⁻¹ Mivel az előző becslés minden n-re jó:

0 < H =

∞

X

n=101

2ⁿ+ 3ⁿ⁺²

1 + 6ⁿ⁻¹ < 60·

∞

X

n=101

1 2

n

= 60· 1

2 101

1−1 2

2.4. Abszolút konvergencia, feltételes konvergencia

Elm→

Abszolút vagy feltételesen konvergens-e az alábbi sor?

14. Feladat:

∞

X

n=1

(−1)ⁿ⁺¹ 2n+ 1 3n−2

Megoldás.

c_n := |a_n| = 2n+ 1 3n−2 =

2 + 1 n 3− 2 n

→ 2 3 6= 0

=⇒ a sor divergens, mert nem teljesül a konvergencia szükséges feltétele.

c