Dahlborg National Research Council, Stockholm, Sweden

K. E. Larsson

Royal Institute of Technology, Stockholm, Sweden

U. Dahlborg

National Research Council, Stockholm, Sweden

and K. Sköld

AB Atomenergi, Studsvik, Sweden

1. Neutron Method 119 1.1. Principles of the Neutron Scattering Method: Observed and Derived

Quantities 119 1.2. Experimental Technique 128

2. Liquid Helium 134 2.1. Static Structure Factor 134

2.2. The Dispersion Relation and Its Related Quantities 136

2.3. Line Width of Excitation Peaks 143

3. Liquid Argon 146 3.1. Atomic Distribution 146

3.2. Atomic Motion 153

4. Hydrogen 166 4.1. Total Cross Section 166

4.2. Differential Cross Section 168

5. Methane 171 5.1. Total Cross Section 171

5.2. Differential Cross Section 172

5.3. Scattering Law 177

References 181

1* Neutron Method

1.1. PRINCIPLES OF THE NEUTRON SCATTERING METHOD:

OBSERVED AND DERIVED QUANTITIES

1.1.1. Introduction

The scattering of slow neutrons has proved to be a very powerful technique in obtaining information concerning the dynamical behavior

119

120 Κ. Ε. LARSSON, U. DAHLBORG, AND Κ. SKÖLD

and the microscopic structure of the condensed state of matter. For other techniques used for this purpose, such as inelastic scattering of light, nuclear magnetic resonance (NMR), and x-ray studies, the time scale is extremely long or extremely short compared to a characteristic time interval in the liquid motion of the order of 10~¹³ to 10~¹² sec.

Thus these techniques fail to be sensitive to the detailed atomic motions in the scatterer. In contrast, a slow neutron of a wavelength comparable to interatomic distances interacts with a scattering atom or system of atoms on a time scale from 0 to about 10~ⁿ sec. This length of observa- tion time permits the slow neutron to see both the high frequency vibratory motions and the elementary diffusive motions with relaxation times of the order of 10~¹² sec.

The purpose of the present chapter is to describe briefly the method of scattering of slow neutrons and to review the results gained on four liquids, namely, helium, argon, hydrogen, and methane. However, first a terminology and a framework has to be established within which the results can be discussed. For a more detailed review of the field the reader is referred to two monographs by Turchin [1] and Egelstaff [2]

and to the proceedings from three symposia sponsored by IAEA on this subject [3-5].

The differential scattering cross section per atom is, according to van Hove [6], given by four-dimensional Fourier transforms of correla- tion functions G(r, t) and Gs(ry t)

- g £ = «c²oh^Scoh(K)£o) (1.1)

jnk j — = ßincoh T - ^Incohi*, ω) (1.2)

did αω R0

where

Scoh(K, ω) = r - exp[i(Kr — wt)] G(r, t) dt dt (l-3a) 1 f Sincoh(*, ω) = ^ J exp[i(xr - ωή] G1 r s(r, t) dv dt (1.3b) The functions S, sometimes called ' 'scattering laws," depend only on

the properties of the scatterer; ΫΙΥ. and ϋω stands for the momentum and energy transfers in the scattering process and are given by

κ = k - k0 ω = (ä/2m)(£² - V ) (^{L 4}) where k0 = 2π/λ0 and k = 2π/λ are the initial and final neutron wave

vectors, λ0 and λ are neutron wavelengths, m is the neutron mass, and

2πί is Planck's constant. The coherent and incoherent scattering lengths are aloh and a^coii · The classical interpretation of the correlation functions G(r, t) and Gs(r, t) is as follows:

given a particle at the origin at time zero, Gs(r, t) gives the proba- bility that the same particle is at position r at time t and G(r, t) gives the probability that any particle is at position r at time t.

Other quantities often used in connection with discussions of the scattering law are the intermediate scattering functions corresponding to the spatial part of the transforms just given

/(κ, t) = -!- j dt exp(*xr) G(r, *) (1.5a) and

/s(*, t) = i - J dv exp(mr) Gs(r, t) (1.5b) Particularly the function /(κ, 0) has a clear and simple physical meaning

as discussed later.

The cross section is separated into two parts, the so-called coherent and incoherent cross sections. The properties of incoherence or coherence depend on the details of the interaction between the neutron and the nucleus in the scattering process and will not be discussed here. It is seen from the equations that the self part of the correlation function enters into the incoherent cross section while the coherent cross section is determined by the complete correlation function. Most nuclei scatter both incoherently and coherently. Important exceptions in connection to the present treatment of some simple liquids are the cross sections for hydrogen, which is almost completely incoherent, and for helium, which shows a 100% coherent cross section.

1.1.2. Incoherent Case

In case the scattering nucleus has an incoherent cross section all the motions of the scatterer are revealed in the scattered spectrum. The fact that various atomic motions occur on different time scales is thus most easily and without discrimination seen for this case. The low frequency—

or equivalently the long time motions—corresponding to frequencies smaller than 10¹² cps or to times of about 10~¹² sec or longer, give rise to a more or less narrow peak centered round the ingoing neutron energy and is often called the quasi-elastic peak. The high frequency or short time motions, corresponding to frequencies larger than 10¹² cps

1 2 2 Κ. Ε. LARSSON, U. DAHLBORG, AND Κ. SKÖLD

or times shorter than 10~¹² sec, give rise to a broad inelastic neutron spectrum.

Considerable effort has gone into the interpretation and understanding of the quasi-elastic neutron scattering. Various attempts were made to separate it from the inelastic part, and more or less complex models were created to throw some light on the nature of the diffusive atomic motions.

Particular attention was given to the width of this quasi-elastic peak, which is found to be a function of κ (or the scattering angle). The width is an observable quantity sometimes easy to obtain but mostly rather difficult to define accurately due to the problems involved in the separa- tion of the quasi-elastic peak from the rest of the observed spectrum.

For several simple models the full width (ΔΕ) at half-maximum of the quasi-elastic peak was given as follows:

(a) The simple diffusion model [7]

ΔΕ = MDK² (1.6)

where D is the self-diffusion coefficient.

(b) The simplest jump diffusion models [8, 9]

2ft/ e~^2W

T_Q\ 1 + Z)iA0, 2ft / e~^2W \

"-^("-■nnsd <■·*>

or

ΔΕ

~(>-==r·) <»"·>

where τ0 is the residential time between jumps, 2W'is> the Debye-Waller factor, and / is the jump length.

(c) The modified jump diffusion model [10]

where D0 is a smaller diffusion coefficient describing a slow continuous motion of the vibrating particle during the residential time r0 .

(d) A modified gas model [11]

ΔΕ = 2^(2 In 2)^1/2(Z)/r)¹/²* (1.9)

where r is a delay time before diffusion sets in and which transforms to the simple gas model, if τ = tß = MD/kBT, where M is the atomic or molecular mass. This formula should be valid for somewhat larger K-values and not in the limit κ —> 0.

(e) The complex model [12] involving motions of the center of gravity of the molecule as well as internal atomic motions relative to the center of gravity (such as free or hindered rotations of a simple molecule like CH4). Two extreme cases are:

(i) High viscosity (τ'0 > r0)

AE = — [1 - F(K, I) e x p ( - 2 ^ · - 4We)] (1.10)

Too

where l/r00 = l/r0 -f l/^o ^{a n}d ^To^^{s t n e} residential time for a proton before jumping, r'0 is the time for which free diffusive motions of the molecule are hindered, and 2Wi and 2We are the Debye- Waller factors for the proton and center of gravity vibrations, respectively; F(K> I) is an integral which mainly depends upon the K-value and the internal protonic jump length (for instance partial rotation), the value of which varies between 1 and 0.

It may also be of oscillatory character.

(ii) Low viscosity τ[ ^> r'0 and r0

ΔΕ = 2h[DK* + (l/r0) - F(Ki I) exp(-2^·)] (1.11) where τ[ is the time for which the molecule is free to diffuse

(a fraction of time of ^/(TQ + τ[) &t I for case (ii)).

A variety of models were thus created to assist in the understanding of the incoherently scattered quasi-elastic neutron intensity from a liquid, and attempts were made to relate its width to macroscopic properties such as diffusion as well as to microscopic phenomena such as relaxation time for elementary atomic or molecular steps of motion.

In connection with experimental and theoretical neutron scattering studies it was shown [13] that in the absence of interference scattering a generalized frequency distribution p(ß) in a liquid, corresponding to the distribution of normal modes f(ß) in a solid, can be derived from the inelastic neutron spectrum through

p(ß) = ß* lim (1/α) SincohK ß) (1.12)

where α = #²/c²/2 MkBT and β = fi<jù\kBT. For a solid the relation between p(ß) and f(ß) is

l*n = -£m ^(L13)

Thus, p(ß) may be obtained directly from a series of scattering measure- ments for very small momentum transfers. The value of p(0) is shown to

1 2 4 Κ. Ε. LARSSON, U. DAHLBORG, AND Κ. SKÖLD

yield the self-diffusion constant through p(0) = MD/nkBT. The observed similarity between liquid and solid state frequency distributions has stimulated the use of solid state formalism in the derivation of f(ß) from the inelasticly scattered neutron spectrum. This method, which is identical to a phonon description of the atomic motion, is of course to be considered merely as an aid in the interpretation and may not, without a careful and critical comparison to other evidences, be used as a proof for the existence of phonons or quasi-phonons in a liquid.

In general, the atomic motion revealed in the inelastic part corresponds to energy transfer also observable by use of other radiation scattering techniques. Thus in the more general case the energy transfer observed in the inelastic neutron spectrum is also seen in light scattering (infrared or Raman spectra). The main difference is that in neutron scattering not only energy transfer but also momentum transfer is involved.

1.1.3. Coherent Case

In the case when coherent scattering occurs or in the more general case of a mixed coherent and incoherent scattering (such as for liquid argon) one has to resort to the general definitions of the cross sections as Fourier transforms of the correlation functions G(r, t) and Gs(r, t).

According to the definitions given above a complete experimental mapping of the scattering functions £(κ, ω) and Ss(x, ω) allows a deter- mination of the correlation functions by way of a Fourier inversion of the data.

From the definitions of the correlation functions it is found that

Gs(r,0) = 6(r) (1.14a)

G(r,0) = 8(r)+g(r) (1.14b) where g(r) is the static pair distribution function, which gives the average

particle density around a given particle at the origin. This function is well known from x-ray studies of liquids. Experimentally, G(r, 0) is obtained from an angular distribution study. Evidently one obtains for a liquid

-^JFT = ^acoh J S(yty ω) άω = a²e0h j exp(ntr) G(r, 0) dv

= <&Λ/(Χ, 0) = <z²coh(l + J exp(mr)[£(r)</r]) = 4oh[l + y(x)] (1.15a) From a complete mapping of S(x, ω) the pair distribution function ^(r) is obtainable by a Fourier inversion of the integral over all energy transfers tiw. In general, a direct angular distribution study by use of neutrons—a determination of dacoh/dü—gives the desired liquid

structure factor 1 + γ(χ) only if the ingoing neutron energy E0 (or fiœ0) is much larger than all energy transfers occurring in the energy exchange between the neutron and the liquid system. This follows from the fact that in general the differential cross section cPojdQ dœ contains the factor k/k0 = [(ω + ^ωο)/^ωο]1 / 2 a s a multiplier in front of £(κ, ω). Thus, only if ήω0 ^> ϋω one finds that

d*a , 2

J ^ aCOh

dQdi j S(yt}œ)dco (1.15b)

This is called the "static approximation,'' valid only if fiœ0 ^> fiœ.

A few attempts were made to create models for the liquid atomic motion such that theory could predict S(x, ω). In general, 5(κ, ω) is determined by the correlation function G(r, t) = Gs(r, t) + Gd(r, i) where Gd(r, t) is the time-dependent pair correlation function. The main problem was to find a reasonable and physically plausible construc- tion for Gd(r, t). The oldest attempt—the so-called convolution ap- proximation—describes Gd(r, t) as a convolution of G8(r> t) with the static pair correlation function g{r). This results in a cross section [7]

i2 2 J 2

d crCOh tfcoh & tfincoh π ι / vi /i i^:\

ΊΩΪ^

= < ^

+ *

(

>

which, however, has failed to describe the observed £(κ, ω) when exposed to a critical test, the main reason being that due consideration is not given to the existence of an atom at the origin. In fact, the motions of the atom at the origin and the neighboring atoms might be—and most probably are—coupled, such that correlated motions occur. Assuming that correlated motions of the phonon type occur within a correlation range R a round each atom in the liquid, a correction to the convolution approximation was created to yield a cross section formula [14, 15]

J 2 2 J2

u o"coh #coh « °"incoh Γ 1 ι / \ ■ i ar/r> νι / ι ι τ \

where q is the absolute value of wave vector of a quasi-phonon of energy ϋω\ L(R, K, q) is a complicated function given by

3R r°° 1 r^+q (r / R² \

m K

'

^ v z /„***>

2ç L I t

( - T

« -

*)

- e x p ( - f (K + k + χή]

- [

P ( - f (* -

)

) -

P ( - ? (* + *)

)] j äx (1.17b)

126 Κ. Ε. LARSSON, U. DAHLBORG, AND Κ. SKÖLD

Still a third attempt was made to calculate the cross section on the basis of an extreme polycrystalline model for a liquid with the assumption that not only is there a correlation range R (within which ordered and coupled atomic motion occurs for a time τ) long enough to permit the development of quasi-phonons, but there is also a geometrical order with a—perhaps partly destroyed—regular lattice structure. This rather extreme quasi-crystalline model also predicts a dependence of cross section on the polarization of the phonons. The cross section is given by Egelstaff [16]. (For a review of this and other models the reader is referred to Dahlborg and Larsson [17].)

J 2 2 J 2

u aCoh #coh ^a O'lncoh ~/ ^\ /i ιο \ Z(q, /c, Θ) (1.18a) dQ doj ^incoh άΩ d(

where Z(q, /c, Θ) is a dynamic liquid structure factor in a simplified way dependent also on the angle Θ between the phonon polarization vector eq and the direction eK of the momentum transfer vector κ. Here, Z(qy Ky Θ) is given by

with cos Θ = eq · eK for the longitudinal vibrations and sin Θ = eQ · eK

for the transverse vibrations; rm i n and rm a x are obtained from

K — q K + q n 1 Q v

Tmin = —^ rm a x = -7J (l.löC)

The limits within which scattered intensity is allowed are then identical to the corresponding limits in the case of a polycrystalline solid for which intensity corresponding to the Bragg reflection rhkl and a certain q value occurs between the limits {27rrhkl -f- q) and (2πτΜΙ — q). The two later models have so far had some success in picturing the observed S(K> ω).

For a quantum liquid such as helium below the λ-transition a dispersion relation for the single excitations is theoretically well established, and such dispersion relations were experimentally determined. Above the λ-transition in helium and for other normal liquids such as condensed argon, the definition of a dispersion relation is not clear because the meaning of single excitations is unclear in a medium so highly excited that the interactions between the excitations make their lifetimes and mean free paths small, perhaps smaller than or comparable to their oscillation period and wavelength, respectively. Nevertheless, attempts were made to define dispersion relations ω = w(q) for simple liquids

such as argon. Such attempts are logically motivated from the possible success of polycrystalline models for liquids. A more detailed discussion for the dispersion relations is given in connection to the presentation of the results on liquid helium and liquid argon.

1.1.4. Some General Rules

From the discussion given it is clear that the scattering functions 5(κ, ω) may not so far be calculated from first principles. Only by use of phenomenological models may some qualitative and simple quantitative deductions be made. It was, however, shown that the scattering functions have to obey exactly some very general and simple rules. These rules are as follows:

(a) The detailed balance condition relating the energy loss and gain parts of the scattering functions and the cross sections:

S(H, -ω) = exp ( - - f ^ ) S(x, ω) (1.19) and

σ( £0- + £ , Ω0- > Ω ) σ ( Ε - * £0, Ω - > Ω0)

E exp[-ElkBT] E0 txp[-E0lkBT] ^ ' ^ (b) The sum rules and the moment relations. Defining

<ωη> = f ωη£(κ, ω) dœ (1.21)

the most important relations are:

<w°>incoh = 1

<>°>coh = 1 + y(*)

UK²

<w>incoh = <>>coh = ^ f n γ£\

<<^>incoh = -jÇj- κ^Δ kM 1 + γ(κ) BT K²

where M is the mass of the scattering atom. In the derivation of the second moments the quantum effects and the recoil of the atoms have been neglected. The higher moments depend implicitly on the internal potential energy of pairs and are very involved. In the present status of

128 Κ. Ε. LARSSON, U. DAHLBORG, AND Κ. SKÖLD

neutron spectroscopy they are of little interest because so far enough accurate data have not been obtained. The relations given above give little information about £(κ, ω) itself but merely serve as a check of the consistency of different theoretical models and of experimental results.

1.2. EXPERIMENTAL TECHNIQUE

The main experimental problem in the neutron scattering techniques is to obtain a beam of incident neutrons with a well-defined energy and to determine the energies of those neutrons scattered in a selected

FIG. 1. Vertical section of the slow chopper time-of-flight spectrometer in Stockholm (from Larsson et al. [18]).

direction from the sample. These two determinations give the energy and momentum transfers from the conservation relations (Eq. 1.4).The problems of monochromation and of energy and angular analysis can be met in several ways and some of them will be briefly discussed here in order to elucidate the reliability of different types of measurements.

In Table I some pertinent data for five different types of neutron spectrometers are collected. The reason for this particular choice of instruments is that with their aid some of the most extensive measure- ments were made on the four liquids to be discussed below. Most of the data in Table I have been taken from a compilation of Brugger and Harker [23] of time-of-flight neutron spectrometers. The operational properties of different instruments are now well understood, while some measurements performed at an early stage can be impaired by systematic errors.

Table I needs some explanatory remarks. The monochromatizing and analyzing actions can be performed by the time-of-flight technique, by the diffraction technique, or by a combination of the two. The equipment shown in Fig. 1 utilizes the fact that the total cross section of a polycrystal possesses a cut-off energy above which the cross section is very high.

Thus if a piece of polycrystalline beryllium is placed in a neutron beam with a Maxwellian energy distribution, only neutrons with energies less than about 5 meV will be transmitted. The energy spread of the neutrons hitting the sample is rather large, about 5 0 % . After the scattering in the sample, the energy of the neutrons in a selected direction is recorded by the slow chopper time-of-flight technique. In spite of the large energy spread of the incident neutrons a relatively good resolution for elastic scattering is achieved by making use of the sharp filter cutoff. However, the analysis has to be performed with the greatest care.

An improvement of this equipment is the apparatus shown in Fig. 2, where the monochromating properties of a chopper is utilized. This spectrometer was used for extensive measurements on liquid argon.

The chopper is placed before the sample, thus performing the combined action of reducing the width of spectrum of incident neutrons and triggering of a time-measuring device. An advantage of this equipment compared to the previous spectrometer is that, as the pulsing device is placed before the sample, simultaneous measurements in many scattering angles can be made. The uncertainty in energy of the impinging neutrons is about 1 5 % at 5 meV.

In their measurements on methane, Harker and Brugger [24] used the phased rotor velocity selector shown in Fig. 3. The principle is the following: The first chopper (A, Fig. 3) produces a short burst of neutrons, while the second (Z), Fig. 3), placed a certain distance from A,

TABLE I CHARACTERISTICS OF SOME NEUTRON SPECTROMETERS o Type of spectrometer and location Slow chopper, Stockholm, Sweden [18] Semimonochromating chopper, Studsvik, Sweden [19] Phased chopper velocity selector, Idaho Falls, USA [20] Triple axis crystal spectrometer, Chalk River, Canada [21] Rotating crystal spectrometer, Chalk River, Canada [22]

Monochromating device Be filter Be filter plus chopper Phased rotors Single crystal Al (111) Single crystal Al (111)

Analyzing device Time of flight Time of flight Time of flight Single crystal Pb(lll) Time of flight

Width of the spectrum of incident neutrons with energy E0 meV Resolution of analyzer for elastic scattering

Resolution of analyzer for inelastic scattering to energy Ef meV 50% at5meV 15% at5meV Variable. Typical value: 2% at 55 meV Variable

4% for E0 = 5 meV 13% for£0~ 4meV and Ef = 25 meV 4.5%forE0 = 5meV 2.4 % for EQ = 5 meV and Ef = 25 meV 10% for £Ό = 55meV 4.8 % for E0 = 55 meV and Ef = 25 meV 3.3 % for £0 = 5 meV

> CO O 2 > x r w o 0 > ö O: ö 1 % for E0 = 5 meV -1 % for 5 < E0 < 50 meV 3.4 % for E0 = 5 meV and Ef = 25 meV

Detectors

/

H Lead

^ Iron ES3 Borate paraffin Ξ Water

Sample Chopper Be-filter Be-filter

fcmWWKfl

FIG. 2. Horizontal section of the time-of-flight spectrometer in Studsvik, Sweden (from Holmryd et al. [19]).

ROTATING COLLIMATORS B E A M . < * \ HOLE X M <Λ PLUG " ^v

FITTED SHIELDING

VACUUM PUMP

SHIELDED SCATTERING

ROOM

COUNTERS

BEAM MONITOR

FIG. 3. Cutaway drawing of the MTR velocity selector (from Brugger and Evans [20]).

1 3 2 Κ. Ε. LARSSON, U. DAHLBORG, AND Κ. SKÖLD

opens a preset time after the burst is produced at A. Thus by using a given distance and time lag between the choppers a burst of neutrons with a certain energy is obtained. The aim of the two rotating collimators is to reduce the background. The resolution of this instrument is rather poor as seen in Table I. Its main advantage lies in the possibility of

easily changing the wavelength of the incident neutrons, thus allowing measurements of 5(κ, ω) over a wide region of (AC, o>)-space.

Another method of obtaining a monochromatic neutron beam is by use of single crystals. An instrument of this type is the double crystal spectrometer used by Henshaw and Woods [21] for measurements of the dispersion relation in liquid helium (Fig. 4). From the white neutron beam only neutrons with a specific energy are reflected in a certain direction as given by the Bragg formula. The energy analysis of the neutrons scattered in the sample is made by the second spectrometer.

Neutrons from higher order reflections are eliminated by inserting a beryllium block in the channel leaving only cold neutrons for first- order reflection.

The rotating crystal spectrometer shown in Fig. 5 is a combination of the time-of-flight technique and the crystal technique. The mono- chromatization and the pulsing of the neutrons are performed by a rotating crystal. Each time a set of crystal planes satisfies the Bragg condition a burst of monoenergetic neutrons is produced. This technique

FIG. 5. Schematic diagram of the Chalk River rotating crystal spectrometer (from Woods [25]).

1 3 4 Κ. Ε. LARSSON, U. DAHLBORG, AND Κ. SKÖLD

was used for measurements on helium by Woods [25] and on methane by Dasannacharya and Venkataraman [26].

When comparing the various instruments of Table I it should be remembered that the higher the resolution, the lower the useful neutron flux. The cold neutron technique making use of the full beryllium-filtered neutron spectrum as the incident beam has a relatively limited usefulness but gives a high intensity. The double rotor system or a rotating crystal spectrometer tends to give one or two powers of ten lower intensity, which thus is the prize paid for the higher resolution.

2* Liquid Helium

2.1. STATIC STRUCTURE FACTOR

As discussed briefly in the preceding section, information about the atomic distribution in liquids can be obtained from a neutron diffraction pattern. Measurements performed on liquid helium cover a wide range of temperatures as well as pressures. The three neutron diffraction studies published were all made at Chalk River [27-29], where also most measurements on inelastic scattering were performed.

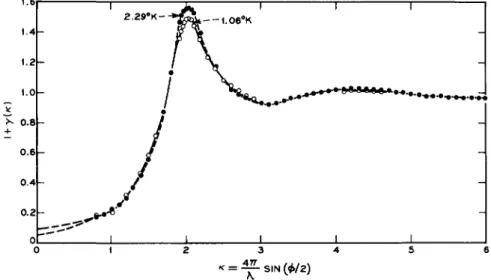
Figure 6 shows the liquid structure factor 1 + y(^K) as a function of

I.61 1.4 1.2 i.o|

^ 0.8|

+ 0.6 0.4 0.2

* = ^ S I N (φ/2)

FIG. 6. The liquid structure factor for liquid helium under its normal vapor pressure at ( · ) 2.29°K and ( o ) 1.06°K. The effect of the λ-transition causes a lowering and broadening of the main maximum (from Henshaw [28]).

the momentum transfer for liquid helium under its normal vapor pressure at 2.29° and 1.06°K (that is, on both sides of the A-transition which occurs at 2.19°K). The wavelength of the incident neutrons was 1.064 A. The momentum transfer κ is given by κ = 4π/λ sin <f>/2y where λ is the neutron wavelength and φ is the scattering angle. Unless the scatter- ing is elastic κ is not given as above, but this condition is nearly fulfilled if the ingoing neutron energy E0 is much larger than the possible energy transfers ΔΕ in the scattering system (E0 ± ΔΕ ^ E0). The circles do not correspond to measured intensities but are taken from smooth curves obtained from the experimental data after correction for experimental effects and for multiple scattering. The broken curves for small /c-values are extrapolations from the first experimental point to the known value of the zero angle scattering L0 given by L0 — nkBTifjT, where n is the particle number density and ψτ is the isothermal compressibility. From Fig. 6 it is seen that between the two temperatures no drastic change occurs when passing the λ-point but rather small differences in detail occur in the region of small /c-values. The main peak is at κ = 2.03 A^{- 1} beyond which there is a small second maximum at κ — 4.3 A^{- 1}. The ratio of the main peak height of the curve at 2.29°K to that at 1.06°K is 1.047. This is close to 1.05 which has been deduced from x-ray measure- ments. It is interesting to note that there is an indication of a small bump at κ ~ 0.8 A^{- 1} in the 1.06°K measurement. The experimental error in this /c-range is, however, comparatively large so nothing definite can be concluded about its reality.

In Table II the main results are collected from neutron diffraction work on liquid helium. It is worth noting that the data of Hurst and Henshaw [27] are not corrected for multiple scattering effects while the others are. This is probably the reason why these earlier results system- atically differ from the more recent ones.

The distribution function 4nr[p(r) — p0], where r is the distance from the atom chosen as origin, p(r) the atomic density at distance r, and p0 the mean atomic density in the liquid, is obtained from the liquid structure factor 1 + y(^K) through

4nr[p(r) - Po] = - f κγ(κ) sin(n<) άκ (2.1)

π J o

As it is only possible to cover a finite /c-region experimentally, errors might be introduced by taking the Fourier transform integral from zero to infinity. Although the uncertainties of some quantities derived from the transform may be quite large, some qualitative conclusions can be drawn:

136 Κ. Ε. LARSSON, U. DAHLBORG, AND Κ. SKÖLD TABLE II

RESULTS FROM LIQUID HELIUM ATOMIC DISTRIBUTION FUNCTIONS BY NEUTRON SCATTERING

Number of Position Liquid Position of nearest where

temp. Pressure Density maximum neighbors from 4irrp(r) rises Ref.

(°K) (atm) (gm/cm⁸) in 4πτρ(τ) symmetric peak from zero

1.06 1.65-2.25

2.29 4.24 5.04 2.05 4.2

NVP NVP NVP NVP NVP 15.0 51.3

0.145 0.146 0.146 0.125 0.095 0.166 0.184

(A)

3.80 3.70 3.80 3.72 3.94 3.60 3.55

in 4nrp(r) (atoms)

9.8 8.6 9.7 8.1 7.0 9.2 10.2

(A)

2.35 2.25 2.40 2.25 2.20 2.35 2.26

[28]

[27]

[28]

[27]

[27]

[29]

[29]

(a) The nearest distance of approach is nearly independent of density, approximately 2.30 A.

(b) The mean radius of the shell of nearest neighbors is decreasing with increasing density from about 3.9 A at p = 0.095 gm/cm³ to about 3.5 A a t p = 0.184 gm/cm³.

(c) The number of nearest neighbors is increasing with increasing density.

(d) From Fig. 7 it is obvious that a change in density induced by pressure variation has a larger effect on the radial distribution function than the corresponding change caused by temperature variation. Not only is the number of nearest neighbors increased with increasing pressure but also a more marked structure further out in the liquid seems to be introduced.

2.2. T H E DISPERSION RELATION AND ITS RELATED QUANTITIES

In 1957, Cohen and Feynman [30] suggested that it should be possible to determine the energy-momentum relation for the elementary excitations in liquid He II by inelastic scattering of slow neutrons. The experiment should in principle be of the same type as those which at that time already had been performed in order to measure dispersion relations in crystals. Before 1957 some unsuccessful experiments [31, 32]

0 1 2 3 4 5 6 7 β 9 10 RADIAL SPACING (ANGSTROMS)

FIG. 7. The radial distribution functions 4nrp(r) for five different densities. The straight lines are 4irrp0 (from Henshaw [29]).

were performed to establish an effect of the λ-transition in the total cross section. As these now are of less interest they will not be discussed here.

In 1960, Palevsky [33] made a summary of these early results and also of the inelastic scattering experiments which had been performed at that time.

138 Κ. Ε. LARSSON, U. DAHLBORG, AND K. SKÖLD

A typical scattering pattern taken from Henshaw [34] is given in Fig. 8 where the spectrum of 4.14 A neutrons scattered from liquid helium at different temperatures using a rotating crystal spectrometer

44 40 36 32 28 24

6

* 16|

12 8 4

0|

to&S+H******

J_ _L 3.6 3.7 3.8 3.9 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9

NEUTRON WAVELENGTH(ANGSTROMS) 5.0 5.1 5.2 5.3 FIG. 8. The spectrum of neutrons scattered from liquid helium at several temper- atures using a rotating crystal spectrometer. Angle of scattering, 80°. The vanadium curve gives the wavelength distribution of incident neutrons uncorrected for the resolution of the instrument. The liquid helium curves have been corrected for the wavelength sensitivity of the instrument and normalized on the basis of liquid density. The curves at 2.08° and 4.2ΓΚ have been corrected for instrument resolution (from Henshaw [34]).

is plotted. The operation of a rotating crystal spectrometer has been discussed above. The vanadium curve gives the wavelength distribution of the incident neutrons. The change in energy E and momentum p of the neutron in the scattering process which equals the energy and momentum of the created excitation is calculated through the con- servation formulas

F

-Jt(J LA

2m \ V A,¹ /

87r²COS<ft-|^1/a

(2.2a) (2.2b)

where λ^ and Xf are the incident and scattered neutron wavelengths, φ is the scattering angle, m is the neutron mass, and h is Planck's constant.

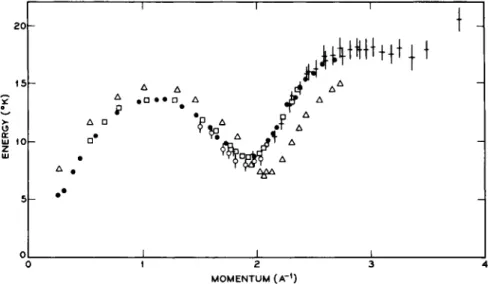
The first result was published by Palevsky et al. in 1957 [35] and demonstrated the existence of excitations with long mean free paths in He II. Since then the dispersion relation in He II has been determined with high accuracy at different temperatures and pressures [21, 25, 34, 36—41]. In Fig. 9 some measured points obtained from the liquid at its

20r-

15

m 10

z

Δ

P

Δ D

L D·

•

1 ··

1 1 1

Δ Δ ,4 Δ^Δ

»Q · · D Δ J f Δ

V'*

1 1 1

71

0 1 2 3 4

MOMENTUM (A^{- 1})

FIG. 9. The dispersion relation at different temperatures and pressures. The data, which are taken from different publications, do not pretend to be complete, ( θ ) Palevsky et al. [37] NVP, (□) Yarnell et al [39] NVP, ( · ) Henshaw and Woods [21] NVP, ( + ) Woods [25] NVP, and ( Δ ) Henshaw and Woods [40] 25.3 atm.

normal vapor pressure and at 25.3 atm are plotted as a function of the momentum pjfi. The energy is given in degrees Kelvin. It is clear that the results are fitted very well by a curve of the shape predicted first by Landau [42, 43] and later by Feynman [44]. On the whole the agreement between different measurements is extremely good, which is very satisfactory because a variety of different experimental methods were used (cold neutron time-of-flight spectrometer, cold neutron crystal spectrometer, rotating crystal spectrometer, and triple axes crystal spectrometer). All results at normal volume and pressure (NVP) are not performed at one temperature but fall in the temperature interval 1.1 °K < T < 1.6°K. We have preferred not to try to adjust the data to one temperature as the complete temperature dependence of the excita-

1 4 0 Κ. Ε. LARSSON, U. DAHLBORG, AND Κ. SKÖLD

tion curve is unknown. From fitted curves through the measured points at the two pressures the following facts can be extracted:

(a) The slope of the curves for small momenta, the phonon region, corresponds very closely to the measured velocity of ordinary sound in He II.

(b) The maximum of both curves fall at E ~ 13.8°K and

Pin~ l.io

(c) The minimum of the curves, the "roton" part, may, according to Landau, be fitted by a theoretically predicted parabola

Ε = Δ+ ^{Ρ~μΡο)2 (2.3)

within a very narrow interval. In Table III values of the parameters

TABLE III

PARAMETERS OF THE ROTON MINIMUM

Experimentalist

Palevsky et al., 1958 [37]

Larsson and Otnes, 1959 [38]

Yarnell et al, 1959 [39]

Henshaw and Woods, 1960 [40]

Henshaw and Woods, 1961 [21]

Temp.

(°K) 1.44 2.03 1.1 1.6 1.8 1.1 1.12

Pressure Δ (atm) (°K) NVP

NVP NVP NVP NVP 25.3 NVP

8.1 ± 0.4 6.7 ± 0.3 8.65 ± 0.04

8.43 8.15 7.0 8.65 ± 0.04

Po/à (A"¹) 1.90 ± 0.03 1.94 ± 0.02 1.92 ± 0.01 1.92 ± 0.01 1.92 ± 0.01

2.05 1.91 ± 0.01

( % e ) 0.16 ± 0.02 0.13 ± 0.02 0.16 ± 0.01 0.16 ± 0.01 0.16 ± 0.01

—

0.16

obtained by different experimenters are collected. Unfortunately, all the experiments have been performed at different temperatures except for those of Yarnell et al. [39] and Henshaw and Woods [21] which, however, show remarkable agreement. The data of Palevsky et al. [37] seem to fall somewhat below the others. This is probably a pure experimental effect because enough consideration has not been given to the influence of the (although small) transmission of a 20-cm-thick Be filter between 3.58 and 3.95 A.

(d) The slope of the NVP curve after the minimum is equal to or slightly less than the slope at very small momenta. For the liquid at

25.3 atm, however, the slope is well below the one corresponding to the velocity of ordinary sound at this pressure.

(e) The NVP curve has a plateau at 17.9°K for 2.7 < p\fi < 3.5 A"¹ and shows a tendency to rise for larger values of pjh. The energy of the plateau is approximately twice the energy at the roton minimum.

However, Woods claims a definite suspicion that the energy of the plateau (17.9 ± 0.6°K) is significantly greater than 2Δ (17.3°K). The 25.3-atm curve shows a tendency to flatten off in the same way, but measurements for very large momenta are missing. The limiting value must in this case be larger than 2Δ (14.0°K) as the last measured point is at 15.0°K.

A measurement of significance for the understanding of excitations in normal liquids was made by Woods [45] who studied the temperature dependence of a long wavelength phonon by use of a rotating crystal spectrometer. As mentioned above the relation E = cp> where c is the velocity of ordinary sound, was found to hold at 1.1 °K for small momenta.

Below the λ-point in the superfluid state the existence of a phonon is accepted, but above the λ-point in He-I, which is a normal liquid, the existence of phonons is still partly an open question. The results given in Fig. 10 clearly show that for temperatures up to 2.57°K long wave- length excitations with momentum of 0.38 A^{- 1} exist in the liquid and that the velocity of the excitation is the same as the velocity of ordinary sound, represented by the broken curve, or slightly higher. No change

_ 300

It

>

1.0 1.5 2.0 2.5 TEMPERATURE ( "K )

FIG. 10. Phonon velocity calculated from the observed neutron distributions com- pared with the measured velocity of sound. The vertical bars on the points correspond to the full width at half-maximum of the peaks. The instrument resolution is 2°K and is the width observed at temperatures below 1.9°K. The broken curve represents the measured velocity of ordinary sound. The point at 1.1 °K is taken from Henshaw and Woods [21], while the other data ( o ) are taken from Woods [45].

1 4 2 Κ. Ε. LARSSON, U. DAHLBORG, AND K. SKÖLD

is seen at the λ-point. Also, the widths of the neutron distributions are fairly small indicating a relatively long mean free path. Even above 2.57°K peaks were found in the scattered neutron distributions, but the uncertainty in assigning a definite energy was too large due partly to the increasing importance of multiphonon interactions.

Measurements of the excitation energy in the momentum range corresponding to the roton minimum on the other hand show a very strong temperature dependence. A systematic study of this effect has been made by Larsson and Otnes [38], Yarnell et al. [39], and Henshaw and Woods [21]. The distributions of scattered neutrons corrected for instrumental effects were found to be symmetrical in energy around the mean energy change for liquid temperatures in the range of 1.78° to 4.21 °K. (Note that in Fig. 8 the scattered intensity is plotted in a wave- length scale.) When the temperature is approaching the λ-point, the

"gap" energy is decreasing to about 5°K as can be seen in Fig. 11. At

- 6 o cr >

LU 4

Vf é

h ^{\ t}

2 3 TEMPERATURE (°K)

FIG. 11. The temperature variation of the energy of the excitation with momentum corresponding closely to the roton minimum. The data are taken from different publications: (O) Larsson and Otnes [38], (*) Yarnell et al. [39], and ( · ) Henshaw and Woods [21].

the λ-point a marked change in the rate of variation occurs, and above the transition (that is, for He I) only a slow decrease is seen. In He I the gap energy should not be interpreted as a roton energy but rather as a mean energy change of the neutrons in the scattering process. This mean energy change may be compared to the mean energy change expected if the neutrons were scattered from free helium atoms. It turns out that the mass of such an atom should be 4.2 helium masses at the λ-temperature and then increasing to about 4.6 helium masses at 4.2°K.

This is equivalent to saying that at 4.2°K an apparent collective of

4.6 helium atoms is the neutron scattering unit. When comparing the data in Fig. 11 it is again seen that the results of Larsson and Otnes seem to fall below those of Henshaw and Woods, but as discussed earlier a possible systematic error in their interpretation may be the reason for this discrepancy. The two sets do, however, show the same tendency.

The measurements of the gap energy are all made at constant scattering angle, and any variation of ρ0/ϋ with temperature has been neglected.

This is not strictly correct as the energy and the momentum of a one- quantum peak is coupled via the conservation laws, but as the minimum of the dispersion curve is rather flat the introduced errors are not serious.

As a matter of fact, Yarnell et al. found no variation of p^jfi in the tem- perature range 1.1° to 1.8°K, while Larsson and Otnes found pjfi =

1.94 ± 0 . 0 2 A-¹ at 2.03°K compared to pjfi = 1.90 ± 0 . 0 3 A"¹ at 1.44°K.

Also of interest is the scattering cross section for the production of a single excitation in the liquid. Figure 12 shows the relative differential scat- tering cross section obtained by integration of the intensity under a peak at two different wavelengths of incident neutrons. The data are taken from Henshaw and Woods [21] and Woods [25]. The cross section has a maxi- mum at a momentum of about 2.0 A~l. This number may be compared to the position of the main maximum of the diffraction pattern 2.03 A^{- 1}. It is clearly demonstrated from the figure that measurements at large momenta are very difficult to perform as the intensity (for instance, at pjfi = 3.36 A"¹) is only 1 % of the intensity at pjfi = 2.0 A"¹. This was the reason why Woods could not continue his dispersion curve measure- ment and establish the rise for pjfi > 3.5 A^{- 1} with certainty. At small momenta there is a tendency for a flat maximum.

In 1961, Woods [46] made a measurement to see if macroscopic rota- tion of liquid helium at 1.54°K caused a change of dispersion curve around the roton minimum. No effect was observed.

2.3. LINE WIDTH OF EXCITATION PEAKS

The energy resolution in the experiments on liquid helium has in all cases been about 2°K. This means that a natural line width of an excitation of about 1°K and larger has given an observable broadening of the scattered neutron distribution. If the uncertainty relation ΔΕ - At = 2fi is used with ΔΕ = kBT it is found that the observable broadenings correspond to lifetimes of an excitation in a range smaller than about 2 X 10^{- 1 1} sec.

Unfortunately, line width studies hitherto performed are incomplete and are mostly concentrated to investigations near the roton minimum.

MOMENTUM CHANGE (A"¹) 2.0 2.5 3.0

4 0

1.4

5 0 60 70 8 0 90 100 SCATTERING ANGLE, φ (DEGREES)

Ί — I — I — I — I — I — I — I — I — I — I — I — Γ

MOMENTUM CHANGE (A*¹)

FIG. 12. The relative partial differential cross section for the production of a single excitation in the liquid at two different wavelengths of incident neutrons (from Henshaw and Woods [21] and Woods [25]). (a) Helium temperature 1.6°K, λ0 = 2.77 A and (b) liquid helium temperature 1.1 °K, λ0 = 4.04 A.

1.0 1.5 MOMENTUM (p/fi IN A^-1)

20 2.5

FIG. 13. Energy spread of the excitation spectrum of liquid helium at various momenta and temperatures as inferred from the observed width of the cutoff in the scattered neutron distribution (from Yarnell et al. [39]).

The measurements of Yarnell et al. [39] (Fig. 13) show that the mean lifetime of the excitations are also dependent on the momentum transfer ϋκ. Although the errors are relatively large, it must be concluded that the energy spread of the distributions is less at the roton minimum and is larger both for smaller and larger momentum values. This is valid in the temperature range of 1.1° to 1.8°K.

Figure 14 shows the line width of an excitation with momentum

t^15 x I—

Q

LU

t

,v ^»It

2 3 TEMPERATURE (*K)

FIG. 14. Line width of an excitation with momentum corresponding to the roton minimum as a function of temperature. The data are taken from different publications:

(O) Larsson and Otnes [38]; (*) Yarnell et al. [39], and ( · ) Henshaw and Woods [21].

146 Κ. Ε. LARSSON, U. DAHLBORG, AND K. SKÖLD

corresponding to the roton minimum as a function of temperature.

The data are taken from Larsson and Otnes [38], Yarnell et al. [39], and Henshaw and Woods [21]. The same objections as before can be raised to the Larsson and Otnes results. Also, Henshaw and Woods have not taken into account the variation of the resolution as a function of the energy change of the scattered neutrons. The main features of the two sets of data are, however, the same. The width is continuously increasing up to the λ-temperature where a drastic change of the slope occurs.

In the He I region there is only a slight increase in the slope up to 4.2°K.

Above the λ-temperature the measured widths are in good agreement with the ones calculated for a gas of free atoms. The masses used in this calculation are the ones derived from the measurements of the mean energy change of the neutrons (see discussion in connection with Fig. 11). When comparing Figs. 11 and 14 it is seen that close to the λ-temperature the energy of the roton excitation is about 6°K while the energy width is of the order of 10°K. This observation, taken together with the result that the mean energy transfer as well as the width of the scattered neutron distribution correspond to an apparent recoiling mass of more than four helium masses, indicates that the measured distribution is a multiphonon distribution in which the one quantum component is hidden, its intensity being relatively low and its width very large. This means that the interaction between excitations is very

strong in this momentum region and that the concept of elementary excitations is questionable. On the other hand, in other and denser simple liquids, the concept of quasi-phonons might still be a valuable hypothesis to use in attempts to understand experimental facts. Also, it is to be noted that the measurements of Woods show that the width of an excitation peak with momentum 0.38 A^{- 1} is small even above the λ-temperature.

3+ Liquid Argon

3.1. ATOMIC DISTRIBUTION

Measurements of the atomic distribution in liquid argon have been reported by Henshaw et al. [47], Henshaw [48], and also by Dasannacharya and Rao [49] (henceforth referred to as DR). Henshaw used the conventional diffraction technique in which the total scattered intensity is recorded as a function of scattering angle. The intensity pattern obtained by Henshaw is shown versus κ in Fig. 15 where the error flags include counting statistics only. The data are corrected for background, resolution, and double scattering. A correction is also

FIG. 15. The intensity pattern from liquid argon obtained by Henshaw [48] (dots with error flags) shown together with the curve obtained by Dasannacharya and Rao [49]

(full curve): T = 84°K, λ0 = 1.04 A [48]; T = 85.5°K, λ0 = 4.06 A [49].

applied for the change in the number of scattering atoms with angle.

The wavelength of the incident neutrons was 1.04 A, and it is assumed that the change in wavelength on scattering is small so that the spread of /c-values within the distribution scattered at a certain angle may be neglected (see above discussion). The static approximation is reasonable for wavelengths not much larger than 1 A but becomes rapidly worse when the wavelength increases and cannot be used at all for the wave- length of 4.05 A employed by DR. In this case a mapping of the cross section over the (ω-κ) plane must be made and the integral over ω must then be evaluated at each separate value of κ. The procedure adopted by DR will be considered in detail in connection with the discussion of the dynamical studies below. The result for the intensity pattern obtained by them using 4.06 A neutrons is shown by the solid line in Fig. 15 where it is seen that the two curves are in fair agreement but that minor differences, especially for κ < 1 A^{- 1}, are also observed. The region of K covered in this way by DR is too narrow for a derivation of the atomic distribution function, and the curve that was used for this analysis was obtained by combining time-of-flight data taken with 4.06 A incident neutrons and crystal spectrometer data taken with shorter wavelength incident neutrons. The complete function obtained by DR is shown by the t = 0 curve in Fig. 20 and the function tabulated in Table IV.