Folyamatos őrlési folyamatok számítógéppel segített numerikus vizsgálata

FOLYAMATOS ŐRLÉSI FOLYAMATOK SZÁMÍTÓGÉPPEL SEGÍTETT

NUMERIKUS VIZSGÁLATA

Doktori (PhD) értekezés

Készítette: Dr. Buzáné Kis Piroska

a Veszprémi Egyetem

Informatikai Tudományok Doktori Iskolája keretében A Doktori Iskola vezetője: Dr. Friedler Ferenc egyetemi tanár

Témavezetők:

Dr. László Zoltán egyetemi docens, a matematika tudomány kandidátusa Dr. Mihálykó Csaba egyetemi docens, PhD

Matematikai és Számítástechnikai Tanszék Veszprémi Egyetem

2004

FOLYAMATOS ŐRLÉSI FOLYAMATOK SZÁMÍTÓGÉPPEL SEGÍTETT NUMERIKUS VIZSGÁLATA

Értekezés doktori (PhD) fokozat elnyerése érdekében Írta:

Dr. Buzáné Kis Piroska

Készült a Veszprémi Egyetem Informatikai Doktori Iskolája keretében

Témavezetők: Dr. László Zoltán egyetemi docens, a matematika tudomány kandidátusa Elfogadásra javaslom (igen/nem) ……….

(aláírás) Dr. Mihálykó Csaba egyetemi docens, PhD

Elfogadásra javaslom (igen/nem) ……….

(aláírás) Az értekezést bírálóként elfogadásra javaslom:

Bíráló neve: ……….. igen/nem

………

(aláírás) Bíráló neve: ……….. igen/nem

………

(aláírás)

Jelölt az értekezés nyilvános vitáján ……..…..% - ot ért el.

Veszprém, ………

a Bíráló Bizottság elnöke A doktori (PhD) oklevél minősítése ………

………

Az EDT elnöke

Tartalomjegyzék

Tartalmi kivonat... vii

Abstract ... viii

Zusammenfassung... ix

Bevezetés ... 1

1. Az őrlési folyamatok matematikai leírásainak áttekintése... 3

1.1. A szakaszos őrlés vizsgálata ... 3

1.2. A folyamatos őrlés vizsgálata ... 15

1.3. Alkalmazások és az őrléshez kapcsolódó további kutatások ... 21

1.4. Az irodalom tanulmányozásából levont főbb következtetések, célkitűzések ... 27

1.5. Az alkalmazott kutatási módszerek bemutatása ... 31

2. A folyamatos őrlések leírására kifejlesztett matematikai modellek és tulajdonságaik ... 33

2.1. A nyílt folyamatos őrlés folytonos matematikai modellje... 33

2.2. A zárt folyamatos őrlés folytonos matematikai modellje ... 35

2.3. A folyamatos őrlések diszkrét matematikai modelljei rekurzív lineáris egyenletrendszer formájában ... 37

2.3.1. A nyílt folyamatos őrlés diszkrét matematikai modellje ... 37

2.3.2. A zárt folyamatos őrlés diszkrét matematikai modelljei ... 37

2.4. A folyamatos őrlések mátrix formában megadott diszkrét matematikai modelljei ... 56

2.4.1. A nyílt folyamatos őrlés diszkrét modellje mátrix formában ... 56

2.4.2. A zárt folyamatos őrlés diszkrét modelljei mátrix formában ... 58

2.5. A folyamatos őrlést leíró rekurzív lineáris egyenletrendszerek tulajdonságai ... 62

2.6. A folyamatos őrlést leíró mátrixok tulajdonságai... 65

2.7. A stacionárius állapot ... 68

2.8. A diszkrét modellek főbb tulajdonságai ... 69

3. A numerikus kísérletek eredményei... 81

3.1. A numerikus kísérletek célja, feltevések ... 81

3.2. Numerikus kísérletek ... 85

3.2.1. Numerikus konvergencia-vizsgálat és a modellek alkalmazhatóságának igazolása 85 3.2.2. A modellek alkalmazása az őrlési folyamatok tervezésére és optimalizálására... 90

3.2.3. A fizikai jellemzők, paraméterek hatásának vizsgálata... 107

3.2.4. A tranziens állapot tanulmányozása ... 120

3.2.5. Az irodalomban előforduló állítások szemléltetése, számítások ellenőrzése ... 129

3.2.6. Matematikai állítások, érdekességek illusztrálása ... 132

3.2.7. A modellek további lehetséges felhasználási területei ... 138

Összefoglalás ... 139

Alkalmazott jelölések... 143

Irodalomjegyzék... 149

Az értekezés új tudományos eredményei... 157

Tartalmi kivonat

Folyamatos őrlési folyamatok számítógéppel segített numerikus vizsgálata A disszertáció témája a folyamatos őrlés mindkét típusának, a nyílt és a zárt folya- matos őrlésnek számítógéppel támogatott numerikus vizsgálata.

A szerző a nyílt folyamatos őrlés folytonos matematikai modelljéből kiindulva származtatta a zárt folyamatos őrlés folytonos matematikai modelljét és a számítógépes szimuláció alapjául szolgáló diszkrét matematikai modelleket és elvégezte a modellek matematikai diszkusszióját.

Ennek keretében a szerző megadta a zárt folyamatos őrlés egy folytonos modelljét, amely speciális esetként magában foglalja a nyílt folyamatos őrlés és a szakaszos őrlés modelljét is. Ezt követően bemutatta a folytonos modellből a zárt folyamatos őrlés egy diszkrét matematikai modelljének levezetését, az eredmény egy rekurzív lineáris egyen- letrendszer, amely a szemcsék áramlását és törését valószínűségszámítási értelemben egymást kizáró eseményként írja le. A szemcsék áramlása és törése egymástól független események egyes modellalkotók szemlélete szerint. E modell megadásával folytatódik a dolgozat, majd a rekurzív lineáris egyenletrendszerek mátrix formában való felírása következik.

A szerző igazolta a diszkrét modellegyenletek megoldásának nemnegativitását és a modellekre vonatkozó főbb állításokat. Bebizonyította, hogy bizonyos feltételek mellett vannak olyan őrlések, amikor a malomban minden időpillanatban, illetve a stacionárius állapot beálltát követően állandó az anyagmennyiség. Azt is igazolta, hogy a malomban minden időpillanatban legalább annyi anyag van a zárt folyamatos őrlés esetén, mint a nyílt őrlés esetén, ha e kétféle típusú őrlésnél azonosak a feltételek és az őrlési folyamatok paraméterei megegyeznek és állandók. Képletet állapított meg a zárt őrlés során a malom kezdeti állapotától a stacionárius állapotáig bekövetkező anyag- mennyiség-változásra, valamint az osztályozóból visszatérített szemcsék mennyiségére vonatkozóan. Megállapította, hogyan kell megválasztani a beadagolt friss szemcsék mennyiségét, a malom legnagyobb terhelhetőségének és az osztályozásnak a figyelem- bevételével ahhoz, hogy ne következzen be túltelítődés.

A dolgozat a modellek numerikus diszkussziójával folytatódik. A szerző vizsgálta az őrlés tanulmányozására kidolgozott módszer numerikus konvergenciáját és azt is megmutatta, hogy a modell alkalmazásával szimuláció útján megkaphatók az irodalom- ban publikált tapasztalati eredmények, a modell számítási eredményei az őrlési tapasz- talattal megegyeznek. A szerző numerikus kísérletekkel igazolta a modell alkalmasságát a folyamatos őrlések tanulmányozására és tervezésére. A flexibilis tolerancia módszer alkalmazásával kidolgozott egy eljárást, amellyel megállapíthatók az előírásoknak megfelelő késztermék előállításához szükséges működési paraméterek optimális értékei.

A szerző numerikus kísérletekkel bizonyította, hogy a kifejlesztett szimuláció felhasz- nálható az üzemi őrlések folyamatszabályozásában is.

A dolgozatban bemutatott eljárással a zárt folyamatos őrlést végző hengeres golyós- malmok, kisebb módosításokkal más típusú, a cement- és a vasgyártásban, a kerámia-, a szilikát-, a gyógyszer-, az élelmiszeriparban, valamint az ásványi anyagok előkészítése területén található malmok is modellezhetők.

A dolgozatban bemutatott eredmények azt mutatják, hogy az őrlési folyamatok szimuláció útján való tanulmányozása jelentősen hozzájárul a folyamatok mélyebb megértéséhez és fontos szerepet tölt be az őrlésekhez kapcsolódó feladatok megoldásában.

Abstract

Computer aided numerical analysis of the continuous grinding processes

The object of the dissertation is the computer aided numerical analysis of the open and the closed circuit continuous grinding processes.

The author has developed the continuous mathematical model of the closed circuit continuous grinding process. The elaborated model involves the describes of the batch and the open circuit continuous grinding as special cases.

In order to the simulation based study of the continuous grinding, discrete models have been derived via discretization of the continuous model. The author proved the properties of the discrete models and pointed out the greatly agreement between the calculated and the empirical results.

By means of simulation and statistical evaluation of the results of the simulation runs, the applicability of the developed models for study and design purposes is verified.

With the aid of the presented models various kind of the grindings may be modelled: grindings in ball mills, and some types of grinding in air jet mills. After realizing little modifications of the models the new ones are suitable for simulation of other types of mills found in the plants and the laboratories.

The results presented in the theses show that computer simulation of continuous grindings may advantageously contributes to the deeper understanding of the processes, and may play important role in the solutions of the problems originated from the grinding plants.

Zusammenfassung

Computergestützte numerische Untersuchung kontinuierlicher Mahlprozesse

Die vorliegende Dissertation setzt sich mit der mathematischen Untersuchung kontinuierlicher Mahlprozesse in offenen und geschlossenen Systemen auseinander.

Für das geschlossene kontinuierliche Modell wurde ein diskretes mathematisches Modell hergeleitet. Dieses beruht auf komplexen Differentialgleichungen, die über ein numerisches Verfahren gelöst werden konnten und sowohl die Strömung der Körnchen, als auch deren Bruch berücksichtigen. Strömung und Bruch stellen sich hierbei als unabhängige Ereignisse dar.

Bei weiterer Betrachtung erweisen sich offene kontinuierliche Mahlprozesse als Spezialfälle, die aus dem geschlossenen kontinuierlichen Modell abgeleitet werden können.

Diese Modelle wurden für weitere Betrachtungen auch in Matrizenform dargestellt.

Des Weiteren beschäftigt sich die Arbeit mit der zu wählenden Quantität des Mahlguts.

Als Prämisse gilt hierbei, dass es zu keiner Überfüllung der Mühle kommen darf.

Ebenso ist auf die Belastbarkeit der Mühle zu achten. In diesem Zusammenhang wurden folgende Behauptungen bewiesen:

Werden bestimmte Bedingungen für das einfallende Mahlgut erfüllt, so stellt sich ein dynamisches Gleichgewicht in der Mühle ein.

Haben einfallende Körnchen qualitativ und quantitativ die gleichen Ausgangsbedin- gungen, so ist im geschlossenen Modell zu jedem Zeitpunkt mindestens genauso viel Mahlgut in der Mühle enthalten wie im offenen Modell. Dies bedeutet auch, dass der geschlossene Mahlprozess effektiver ist.

Da der Eigenwert jeder Matrize des kontinuierlichen Mahlprozesses einen Wert kleines als 1 besitzt, hat das entwickelte Modell eine asymptotische Lösung. Dies bedeutet auch, dass der Fall des dynamischen Gleichgewichts bei diesen kontinuier- lichen Mahlprozessen tatsächlich eintritt.

Unter Zuhilfenahme empirischer Daten aus Fachliteratur konnte außerdem gezeigt werden, dass das entwickelte Programm mit der Wirklichkeit übereinstimmt, sodass hieraus ein anwenderorientiertes Programm für die optimale Wahl der Ausgangspara- meter erstellt wurde.

Mit der vorgestellten Methode, Mahlprozesse zu untersuchen, können verschiedene Mühlen bezüglicher ihrer Wirtschaftlichkeit (Ausnutzung von Rohstoffen und Energie) und hinsichtlich des Umweltschutzes (Abfallreduzierung und –vermeidung) optimiert werden. Zu diesen Mühlen gehören u.a.: zylindrische Kugelmühlen mit geschlossenen kontinuierlichen Mahlprozessen, „air jet“-Mühlen und Mühlen verschiedener Industrie- bereiche.

Bevezetés

Az őrlés, az aprítás széleskörűen alkalmazott művelet számos ipari területen, a cement- és a vasgyártásban, a kerámia-, a szilikát-, a gyógyszer-, az élelmiszeriparban, valamint az ásványi anyagok előkészítése területén. E sokféle alkalmazásnak meg- felelően különböző méretű és működési elvű őrlőkészülékeket fejlesztettek ki a laboratóriumi kávéfőző méretűektől a több méter hosszúságú és magasságú őrlő- gépekig. A legelterjedtebb típusok közé tartoznak a hengeres, a kalapácsos, a rudas-, a golyós-, a gyöngy- és a légsugaras malmok. Az őrlés nagy energiaigényű művelet, amellyel nagyrészt a feldolgozóipar számára készítenek alapanyagokat, kisebb részben késztermékeket állítanak elő.

Az őrlési folyamat alapvetően kétféle lehet; szakaszos vagy folyamatos.

A szakaszos őrlés során az őrlendő anyagot elhelyezik az őrlőkészülékben, majd a megadott ideig őrlik. Az őrlési idő eltelte után kiveszik az őrleményt a malomból.

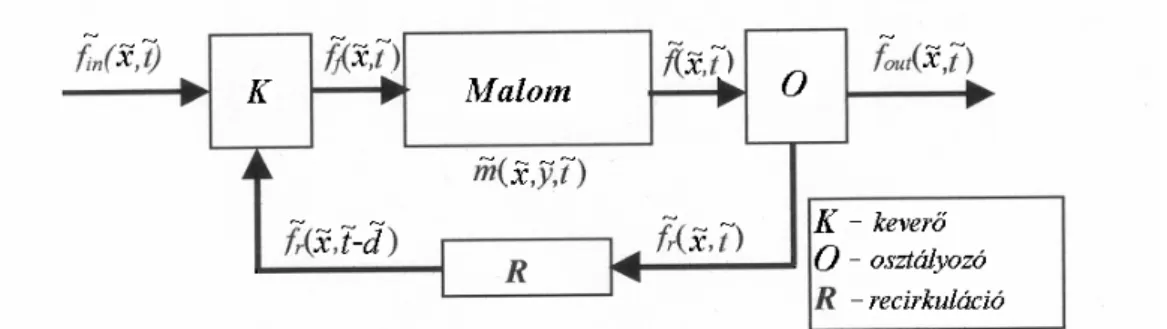
A folyamatos őrlés is kétféle lehet; nyílt folyamatos vagy zárt folyamatos őrlés.

A nyílt folyamatos őrlés esetén az őrlés megkezdésekor a malom lehet üres vagy betöltött állapotban. A malom működése során folyamatosan adagolják be a még őrölet- len anyagot a malom bejáratánál, az anyag a malmon történő végig haladása közben őrlődik, a kijáratánál pedig folyamatosan távozik az őrlemény a malomból. Ezt a folyamatot nyílt őrlési folyamatnak is nevezzük. Gyakran társítanak osztályozót a malomhoz, azzal a céllal, hogy csak a kívánt méretűvé leőrlődött szemcsék kerüljenek ki az őrlési folyamatból. Ilyenkor a malomból az őrlemény az osztályozóba kerül, ott az őrleményt szétválasztják két részre. A már eléggé finomra leőrlődött szemcsék, a

„méreten aluli” szemcsék, alkotják az őrlés végtermékét. Az őrleménynek ezt a részét eltávolítják az őrlési folyamatból. A nagyméretű szemcséket, a „méreten felüli” szem- cséket, újraőrlésre visszatérítik, és a még őröletlen anyaggal, a „friss” szemcsékkel együtt ismét a malomba juttatják. Ezt a fajta őrlést zárt folyamatos őrlésnek, folyamatos recirkulációs őrlésnek vagy körfolyamatos őrlésnek is hívjuk.

A malom kijáratán távozó anyagot őrleménynek nevezzük. Nyílt folyamatos őrlésnél az őrlés szempontjából ez a végtermék, amit készterméknek is nevezünk. Zárt folyamatos őrlésnél viszont megkülönböztetjük az őrleményt a készterméktől. A késztermék vagy röviden a termék, az őrleménynek az a része, amely az osztályozás szerint már elérte a kívánt finomságot.

Egy igen elterjedt malomtípus a hengeres golyósmalom. Maga a malom egy forgó henger, amelyben a különböző méretű golyók a forgás következtében ide-oda ütődnek.

Az őrlőgolyóknak az őrlendő anyaggal történő ütközései idézik elő a malomban lévő anyag összetörését, őrlését. Az ilyen őrlőkészülékben szakaszos, nyílt és zárt folyamatos őrléseket egyaránt végeznek. A dolgozat elsősorban a hengeres golyósmalmokban vég- zett folyamatos őrlések vizsgálatával foglalkozik.

Az őrlés célja a kívánt finomságú őrlemény gazdaságos előállítása, ezért az egyik lényeges kérdés az, hogy hogyan változik az idő függvényében a malomban lévő anyag szemcseméret szerinti tömegeloszlása. A kérdés megválaszolása roppant költséges lenne pusztán fizikai kísérletek elvégzésével kapott tapasztalati eredményekre támaszkodva az őrlőberendezés nagy energiafogyasztása vagy az őrlendő anyag nagy értéke – olykor mindkettő – miatt. Minthogy a matematikai modellezéssel az elvég- zendő kísérletek száma csökkenthető, az őrlés kutatásában az 1940-es évektől egyre nagyobb teret hódít a matematikai modellezés. Az információ technológiában megfi- gyelhető gyors előrehaladás elősegíti a számítógépes szimuláció terjedését az őrlés

tanulmányozása terén is. Végeredményben egyre növekszik a számítógépes szimuláció alapjául vehető modellek iránti igény. A dolgozat az ilyen irányú igénynek a kielé- gítéséhez és az őrlési folyamatok szimuláció útján történő tanulmányozásához kíván hozzájárulni. Az őrlés tág témaköréből a folyamatos őrlések számítógéppel támogatott numerikus vizsgálatát ragadtam ki, mert ez – amint a szakirodalom tanulmányozásából is kiderült – még hiányosan feltárt terület. Az értekezésemben a nyílt folyamatos őrlést a zárt folyamatos őrlés speciális eseteként tárgyalom, nevezetesen, amikor az újraőrlésre visszaadott anyag mennyisége nulla. Megfigyelhető, hogy a szimuláció teret hódít az őrlési folyamatok tanulmányozásán kívül a folyamatok tervezésében, optimalizálásában is. A dolgozatban bemutatott szimuláció felhasználható tervezési és optimalizálási feladatok megoldásában is a késztermékek gazdaságos előállítása érdekében.

A dolgozat első fejezetében a tématerületen született kutatási eredményeket foglalom össze, elsősorban az őrlési folyamatok matematikai leírásai szempontjából.

Áttekintést adok a szakaszos és a folyamatos őrlés matematikai vizsgálata terén, valamint az őrléshez is kapcsolódó további kutatások terén elért tudományos eredményekről. Ismertetem a kutatás célkitűzéseit, bemutatom az alkalmazott kutatási módszereket.

A dolgozat második fejezetében a folyamatos őrlések leírására kifejlesztett matematikai modelleket ismertetem. E fejezet tartalmazza a zárt folyamatos őrlés leírására megalkotott folytonos matematikai modellt, valamint a rekurzív lineáris egyenletrendszer alakjában felírt diszkrét modelleket a származtatásukkal együtt, továbbá a diszkrét modelleket mátrix formában. A folytonos modellből az alkalmazott matematikai levezetéssel előbb a szemcsék törését és áramlását egymást kizáró eseményként leíró modell – Modell I – kapható meg, ebből átalakításokkal a szemcsék törését és áramlását egymástól független eseményeknek tekintő modell – Modell II – származtatható. Az őrlések leírására egyes kutatók a mátrix formában megadott modelleket részesítik előnyben, ezért a diszkrét modelleket ebben az alakban is felírom.

A fejezetet a diszkrét modellek matematikai diszkussziója zárja.

A dolgozat harmadik fejezetében a kidolgozott modellekre alapozott szimulációs eredmények bemutatása következik hét témakörbe csoportosítva. Bizonyítom azt, hogy a kifejlesztett modellek és a szimuláció alkalmasak a folyamatos őrlések tanulmá- nyozására, tervezésére, mert a számítási eredmények a várakozásoknak megfelelőek.

Igazolom, hogy az irodalomból vett mérési eredményekkel megegyeznek a szimulációs eredmények. Bemutatom annak az eljárásnak az alkalmazását, amelyet a malom működési paraméterei értékeinek optimális megválasztására dolgoztam ki, annak érdekében, hogy a felhasználó által megkívánt finomságú őrlemény gazdaságosan elő- állítható legyen. E fejezetben az őrléssel kapcsolatos matematikai jellegű állításokat, érdekességeket is illusztrálok. Végül, vázolom a kidolgozott modellek és szimuláció őrlőüzemi alkalmazási lehetőségeit.

A dolgozat összefoglalással, az alkalmazott jelölésekkel, irodalomjegyzékkel és a tézisek magyar és angol nyelvű ismertetésével zárul.

1. Az őrlési folyamatok matematikai leírásainak áttekintése

1.1. A szakaszos őrlés vizsgálata

A matematikai leírások sorát a szakaszos őrlésre vonatkozó publikációk nyitották meg, amelyek között a sztochasztikus és a determinisztikus megközelítésűek egyaránt megtalálhatók. A determinisztikus megközelítés négy típusa adható meg a szakaszos őrlés esetén attól függően, hogy az idő és a szemcseméret szerint diszkrétnek vagy folytonosnak tekintjük-e a folyamatot. Az őrlési modellek fizikai származtatása mind a négy esetben lényegében azonos elven alapul. Egy szemcseméretet kiszemelve a szemcseméret-eloszlás – vagy a szemcseméret-sűrűség – idő szerinti változását az idézi elő, hogy némely szemcsék kisebb méretűekre törnek a tekintett méretnél, míg a nagyobb méretű szemcsék közül egyesek a kiszemelt méretűvé törnek. Az őrlés egyik legelismertebb kutatója, Austin szerint az 1940-es évektől számíthatjuk az őrlés matematikai leírásának, modellezésének kezdetét (Austin, 1971/72). Ugyanígy vélekednek erről Reid (Reid, 1965), Berthiaux (Berthiaux, 2000), Kostoglou, Karabelas (Kostoglou & Karabelas, 2002) és sokan mások. Az őrlés matematikai vizsgálata során a kutatások főként az őrlemény összetételének – szemcseméret szerinti szám- vagy tömegeloszlásának – meghatározására irányultak.

Az első sztochasztikus modellt a valószínűségszámítás egyik legnagyobb mestere, Kolmogorov publikálta 1941-ben (Kolmogorov, 1941). A szerző igazolta, hogy ha az őrlést, egymást követő nagyszámú törési eseménynek tekintjük és azt is feltesszük, hogy két egyforma darab keletkezik a törés során, továbbá a szemcsék törésének a valószínűsége – méretüktől függetlenül – egyforma, akkor a szemcsék méret szerinti számának eloszlása aszimptotikusan lognormális eloszlású függetlenül a kezdeti eloszlástól.

Kolmogorov elméleti úton vizsgálta az őrlést, vele ellentétben Brown kísérletek végzésével kezdte az őrlés tanulmányozását. Míg Kolmogorov az ismertetett feltételek mellett 1941-ben azt igazolta, hogy az őrlemény eloszlása aszimptotikusan lognormális eloszlású, Brown ugyanebben az évben cikkében arról számolt be, hogy általánosabb feltételek mellett az őrlemény közelítőleg Rosin-Rammler-eloszlású.

Brown 1941-ben megadott modellje idő szerint diszkrét és méret szerint folytonos determinisztikus modell (Brown, 1941), amely Austin szerint az első ilyen modell volt (Austin, 1971/72). A szerző szénőrlési laboratóriumi kísérletek alapján elsőként állapította meg, hogy az őrlemény eloszlása nagyon jól megközelíti a Rosin-Rammler- féle eloszlást. Ezt követően Brown elméleti szempontból is vizsgálta a folyamatot. A kutató feltételezte, hogy mindegyik méretű szénrög, szemcse ugyanolyan arányban törik mindegyik törési ciklusban, vagyis sem a szén keménysége nem változik jelentősen a mérettől függően, sem olyan tendencia nem érvényesül, amely szerint bizonyos szemcsék jobban törnének másoknál. Kutatómunkája során Brown olyan laboratóriumi kísérleti eredményeket is kapott, amelyek azt sugallták, hogy általánosabb feltételek mellett is gyakran tapasztalható különböző anyagok törésekor az őrlemény Rosin- Rammler-eloszlása. Erre alapozva a szerző megjósolta a Rosin-Rammler-eloszlás használatának elterjedését.

Később, 1947-ben az őrlést determinisztikus folyamatnak tekintve Epstein is arra a következtetésre jutott Kolmogorovtól függetlenül (Epstein, 1947, Epstein, 1948), hogy olyan anyagok törésekor, amikor az alábbi két feltétel – A), B) – teljesül, a

szemcseméret szerinti eloszlás jól közelíti a lognormális eloszlást a kezdeti szemcseméret eloszlástól függetlenül.

A) A törési folyamat bármelyik lépése során bármelyik részecske törési valószínűsége független a részecske méretétől.

B) Egyetlen törési esemény során keletkező részecskék eloszlása független az eltört részecske méretétől abban az értelemben, hogy egységnyi mennyiségű L méretű szemcsék törésekor keletkező, a k⋅L -nél kisebb méretű szemcsék súly szerinti frakciója független az L mérettől, ahol 0≤k≤1 .

Az Epstein által megadott egyenlet azt fejezi ki, hogy az őrlés p-dik állapotában az x- nél kisebb méretű frakció mennyisége megegyezik az előző állapotban x-nél kisebb méretű frakció mennyisége és a p-dik állapotban az összes x-nél nagyobb méretű szemcsék közül az x-nél kisebb méretűre törtek mennyisége összegével. Az őrlés p-dik állapotát az őrlés p-dik időpillanatának tekintve, a szerző idő szerint diszkrét és szemcseméret szerint folytonos modellt adott meg.

Az itt szereplő A) feltétel Kolmogorovnál is előfordult, míg a B) feltétel általánosabb Kolmogorov másik kikötésénél, amely szerint két egyforma darabra esik szét a szemcse.

Epstein a törési folyamatot egymást követő törési események sorozatának, míg a méret szerinti változást folytonosnak tekintette. A szerző megjegyezte, hogy mind gyakorlati, mind elméleti szempontból nagyon fontos kérdés, mi történik, ha nem teljesülnek az A) és B) feltételek, ugyanis laboratóriumi kísérletek során a szerző maga is tapasztalta, hogy egyes anyagok őrlésekor a törés valószínűsége a szemcseméret második vagy harmadik hatványával arányos. Fontos kiemelnünk, hogy Epstein kezdte el vizsgálni a törésnek a szemcsemérettől való függését, azonban ilyen esetekben – amikor az A) feltétel nem teljesül – a szerző nem tudta megoldani az őrlemény eloszlásának kiszámítását.

Az aprítás matematikai elméletével Rényi is foglalkozott. Az aprítás folyamatát nagyszámú egymás után következő aprító hatás eredményének tekintette és feltételezte, hogy az egyes aprítási műveletek hatására a szemcsék egyenlő valószínűséggel törnek el, valamint azt is kikötötte, hogy töréskor a szemcsék mérete feleződik (Rényi, 1950).

A szerző cikke első részében Kolmogorovval megegyező eredményt bizonyított a generátorfüggvény módszerének alkalmazásával. Ezután Rényi egy általánosabb törési jelenséget tekintett, olyan törést, amikor a szemcsék egyforma valószínűséggel törnek, de nincs kikötve, hogy a törés utáni méretük feleakkora lesz. Abban az esetben, amikor ismert, de tetszőleges egy megadott szemcseméretről egy megadott szemcseméret- intervallumba törés valószínűsége – azaz teljesen általános törési feltételek esetén – Rényi igazolás nélkül kijelentette, hogy ugyancsak a generátorfüggvény módszerrel megkapható, hogy az őrlemény aszimptotikusan lognormális eloszlású.

Később Filippov méret és idő szerint folytonos, sztochasztikus folyamatként kezelte az őrlést, és bizonyos esetekben az analitikus megoldást is megadta (Filippov, 1961).

Elsőként mutatott rá arra, hogy a sztochasztikus és a determinisztikus megközelítés között világos kapcsolat van: a sztochasztikus esetben a várható értékre kapott egyenlet azonos azzal az integro-differenciálegyenlettel, amelyik az őrlés egyik determinisztikus megközelítésekor, az idő és méret szerint folytonos megközelítésekor adódik. Filippov elméleti eredményeit sem tapasztalati, sem numerikus eredményekkel nem szemléltette.

Laboratóriumi kísérletek alapján az őrleményt sokan találták közelítőleg lognormális eloszlásúnak. Tapasztalati úton azonban az idők során az is kiderült, hogy azt a feltevést, amely szerint bármelyik szemcse egyforma valószínűséggel törik, a tapasztalat a legtöbb esetben nem támasztja alá. Beke szerint (Beke, 1963) az aprító gépekben végbemenő folyamatot az alábbi egyszerű modellel jól szemléltethetjük. Az

aprítás lefolyását oly módon képzeljük el, hogy egy síklapon elterülő halmazra mérünk kalapácsütéseket. Ekkor azonnal érzékeljük, hogy a nagyobb szemcséket, amelyek a halmazból méretük folytán kiemelkednek, nagyobb valószínűséggel éri kalapácsütés.

Tehát az aprítás valószínűsége a szemcsemérettől nem független, azaz a Kolmogorov és Rényi által feltételezett homogenitás nem áll fenn. A fenti „ideális” feltevések abban az üzemi őrlési folyamatban sem érvényesültek, amelyről László Zoltán számolt be (László, 1993). A szerző a cikkében egyben magyarázatot is adott arra, hogy miért állapítottak meg sokszor tévedésből lognormális eloszlást. A valóságban valószínűleg az történhetett – vélekedik László –, hogy kis elemszámú minta alapján állapíthatták meg az eloszlást. A statisztikával foglalkozók ismerik azt a tapasztalatot, hogy egy kis elemszámú mintára többféle eloszlást is lehet illeszteni. Kolmogorov és Rényi dolgozatai is hozzájárulhattak a gyakorlatban a lognormális eloszlás indokolatlan használatához – mutatott rá László.

Idő szerint folytonos és méret szerint diszkrét modellt alkottak meg Sedlatschek és Bass golyósmalmi őrlésre (Sedlatschek & Bass, 1953). A modell alapötlete az a feltevés, hogy annak a valószínűsége, hogy bármelyik szemcseméret szerinti csoportból tetszőlegesen kiválasztott szemcse valamelyik golyóval t+t₁ ideig nem ütközik, független attól, hogy t ideig sem ütközött, vagyis a szemcse múltja nem befolyásolja a jövőbeli ütközéseket. A szerzők kikötései: A szemcseméret szerinti intervallumok hosszainak olyan kicsiknek kell lenniük, hogy bármelyik szemcse – kivéve a legkisebb méretintervallumba tartozót – őrlésekor keletkező törmelékek más-más méretinter- vallumokba kerüljenek. Továbbá, az azonos méretintervallumon belüli szemcsék méretei közötti különbségeknek elenyészőknek kell lenniük a golyók méretéhez képest.

A szerzők a folyamatot lineáris differenciálegyenlet-rendszerrel írták le. Az egyenletek száma megegyezik a méretintervallumok számával. A megoldásban szereplő kons- tansok kiszámítása nagyon komplikált lenne, ezért ezeket kísérleti úton kell meghatározni – javasolták a szerzők. Az elmélet figyelmen kívül hagyja a szemcsék egymással történő ütközése és frikcionálása miatt bekövetkező őrlést, ami a szerzők véleménye szerint jelentéktelen a golyók okozta őrléshez képest. A kikötések teljesítése nehézségekbe ütközhet: egyrészt a méretintervallumok számát nagyon nagynak kellene választani, másrészt az is kérdés, mit értsünk „elenyésző különbség” alatt. A modell nehezen alkalmazható – a kikötések miatt – olyan törés esetén, amikor a szemcséről mindössze parányi részek pattannak le az ütközés hatására, mert a méretintervallumok számát nagyon nagyra kellene választani. A nagyméretű szemcsék őrlése esetén ugyancsak nagyon nagy számú méretintervallumra lenne szükség, ami alkalmazhatósági szempontból szintén akadályt jelent.

Bass idő szerint és méret szerint folytonos modellt is kidolgozott (Bass, 1954). A szerző a szakaszos őrlés leírására időtől függő szemcseméret szerinti tömegeloszlást leíró parciális integro-differenciálegyenletet származtatott, amit elnevezett az őrlés alapegyenletének. Ebben az őrlendő anyag törését és a töréskor keletkező törmelék eloszlását együttesen jellemző, időtől független, tapasztalati úton meghatározandó ε(ξ,α) függvény fordul elő, amely megadja a (ξ,ξ+dξ) méretintervallumba tartozó egységnyi tömegű szemcséből egységnyi idő alatt az (α,α+dα) méretintervallumba tört törmelék tömegét. Tegyük fel, a szemcseméretekre fennáll: 0≤α ≤ξ ≤x_max, ahol

jelöli a legnagyobb szemcseméretet. A szerző szerint az ε(ξ,α) függvény mérések- kel kényelmesen meghatározható, s az alkalmazott függvényközelítések az általános elmélettel összhangban állnak. Jelölje m(x,t) a szemcseméret szerinti tömegsűrűség- függvényt. Az alábbi egyenletet írta fel a szerző:

xmax

∫

∫

⋅

∂ +

∂ ^{x x}

x

d t m x d

x t

x t m

t x m

0

max

) , ( ) , ( )

, ( ) , ) (

,

( ε α α ε ξ ξ ξ.

Bass megadta az alapegyenlet közelítő megoldását zárt alakban arra az esetre nézve, amikor a szemcseméretek kevéssé térnek el a legnagyobb szemcsemérettől. Ekkor az alapegyenlet közelítő megoldása megfelel a félig tapasztalati úton nyert híres Rosin- Rammler-formulának. A szerző közölte, hogy a Rosin-Rammler-formula itt használt alakja az

) (

) ( ) (

) ( ) ) ( , (

t n

t F

x t

n

t e F

x x

t t n x

m ^⎟⎟⎠

⎜⎜ ⎞

⎝

−⎛

⎟⎟ ⋅

⎠

⎜⎜ ⎞

⎝

⋅⎛

=

formula, amelyben két olyan mennyiség, az n(t) és az F(t) fordul elő, melyeket az őrlés minden időpillanatára vonatkozóan újból, egymástól függetlenül meg kell határozni.

Ezek tartalmazzák az időtől való függést. Az n(t) és az F(t) közötti kapcsolatot nem ismerjük, de bizonyára valamiképpen összefüggnek egymással – vélekedik a szerző. A megadott képlettel történő számítási mód csak egy bizonyos, pontosan meg nem határozott őrlési időtartam után használható – írja Bass, azonban ennek az időtartamnak a hossza függ attól, hogy az őrlendő anyag kezdeti eloszlása mennyire közelíti meg a Rosin-Rammler-eloszlást. Csak nagy szemcseméretekre érvényes a képlet, mert ezt a feltevést a levezetéskor kihasználta a szerző.

Bass kis szemcseméretekre is levezette a felírt integro-differenciálegyenlet közelítő megoldását, amely ilyenkor nem adható meg zárt alakban.

A modell gyakorlati alkalmazhatóságát, megbízhatóságát rontják a cikkben előforduló pontatlanságok; nem közölte a szerző, mit értsünk pontosan nagy szemcseméreten, s arra sem utalt, hogyan lehetne megállapítani azt az őrlési időtartamot, amely után az eloszlást a megadott képlettel számolhatjuk. A szerző az ε(ξ,x) függvény alakját nem vizsgálta, a kikötéseket, feltételeket a cikkében nem ismertette, ezek felismerését rábízta az olvasóra. A szakaszos őrlés integro-differenciálegyenlet formájában felírt modellje csak azután terjedt el, miután az ε(ξ,x) függvényt a szelekciós függvény és a törési sűrűségfüggvény szorzataként tekintették – erre később kitérünk.

A szakaszos őrlésre idő szerint és méret szerint is diszkrét modellt Broadbent és Calcott adott meg (Broadbent & Calcott, 1956). Tanulmányukban a szerzők az őrlendő anyag szemcseméret szerinti összetételét – az eloszlást – egy f vektorral jellemezték, amely megadja az egyes szemcseméret tartományokba tartozó szemcsék arányát az összes szemcséhez viszonyítva. A szemcsék törését a B törési mátrixszal írták le, ahol B(i,j) jelöli a j-dik szemcseméretről az i-dikre törő szemcsék arányát egy törési művelet során. Ha az őrlemény eloszlását az n-dik törési művelet után p_n jelöli, akkor p₁=B⋅f, továbbá p₂=B⋅ p₁=B²⋅f, ezt folytatva p_n=Bⁿ⋅f. A szerzők a törési folyamatot egymást követő törési mozzanatoknak tekintették, melyek mindegyikét – a művelet sorszámától független – B mátrixszal jellemezték, majd a törésre vonatkozóan bizonyos egyszerűsítő feltevésekkel élve megadták a törési mátrixnak egy lehetséges alakját.

Ezt követően Broadbent és Calcott ismertették a folyamatos őrlés leírására kifejlesztett idő és méret szerint is diszkrét modelljüket. A szerzők az őrlési zónában végbemenő teljes folyamatot két egymást követő folyamat hatásaként képzelték el. Az első folyamatban kiválasztásra kerülnek azok a szemcsék, amelyek el fognak törni. A kiválasztás leírására a szerzők bevezették a szelekciós mátrix fogalmát, amely egy diagonális mátrix, jelölje ezt S. A fődiagonális elemei rendre azt jelentik, hogy az egyes

mérettartományokba tartozó szemcsék hányad része törik el egy törési esemény során.

A második folyamatban a kiválasztott szemcsék a törési mátrixszal leírt módon eltörnek. Jelölje a törési mátrixot most is B, ekkor B(i,j) most is a j-dik szemcseméretről az i-dikre törő szemcsék arányát jelöli. Az őrlési zónában végbemenő teljes folyamatot – a kiválasztódást és az őrlést együttesen – az alábbi D mátrix írja le, ahol D=B⋅S+(I-S), a jobb oldalon I a megfelelő méretű egységmátrix.

A szerzők egy olyan folyamatos őrlést is tekintettek, amikor osztályozót csatlakoztatnak a malomhoz, ahol az őrleményt szétválasztják „méreten aluli” és „méreten felüli”

részre. Az előbbi az őrlés végterméke, az utóbbit újraőrlésre visszatérítik a malomba.

Ezt a fajta őrlést a szerzők elnevezték zárt folyamatos őrlésnek, melynek speciális eseteként értelmezték a nyílt folyamatos őrlést. A nyílt folyamatos őrlés során egyáltalán nem adnak vissza anyagot a malomba újraőrlésre. Ilyenkor a malomból kifolyó őrleményt teljes egészében „méreten alulinak” tekintjük.

A vázolt zárt őrlési folyamatot Broadbent és Calcott mátrix-egyenletrendszerrel írta le a stacionárius állapotban. A szerzők bár nem definiálták pontosan, mit értenek stacionárius állapot alatt, de utalásaik és a felírt egyenletrendszer alapján a stacionárius állapotot a következőképpen értelmezték: egy bizonyos őrlési idő eltelte után beálló állapot, amikor a malomba bemenő, illetve a malomból távozó anyag eloszlása már nem változik.

A malomba bemenő, illetve a malomból távozó anyag eloszlását jelölje f, illetve p a stacionárius állapotban. Ekkor a malomból távozó anyag eloszlását a szerzők a p=D⋅f egyenlettel írták le, azonban a bemenő anyag eloszlását – f -et – a még őröletlen és a visszatérített anyag együttes eloszlásaként számolták. A késztermék és a visszatérített, a

„méreten felüli” őrlemény együttes eloszlását egyenlőnek tekintették a malomból távozó anyag eloszlásával, p-vel.

A szerzők a zárt folyamatos őrlést csak a stacionárius állapotban vizsgálták. Ebben az állapotban azonban a recirkulációs őrlés olyan, mintha folyamatos recirkuláció nélküli őrlés lenne, mivel a stacionárius állapotban nem változik a malomba bemenő és az onnan távozó anyag összetétele. Így a kutatók valójában a zárt folyamatos őrlés leírását visszavezették egy nyílt folyamatos őrlés leírására.

A szerzők megjegyezték, hogy a szelekciós illetve a törési mátrixot számítani is lehet/lehetne, ha ismerjük/ismernénk a szelekciós illetve a törési eloszlásfüggvényt.

Végül Broadbent és Calcott szénőrlési tapasztalati eredményeiket hasonlították össze a számítottakkal a törési folyamat első néhány lépésére. Megállapították, hogy a felírt modelljeik a szakaszos és a folyamatos őrlések egyaránt valósághű leírásait adják.

A mátrixműveletek könnyen elvégezhetőek, azonban ha a modellben szereplő ismeretleneket – melyek nagyságrendje , ahol n a B mátrix rendje – kísérleti mérési eredményekből kell megállapítani, az veszélyeztetheti a modell alkalmaz- hatóságát, mert egyrészt rengeteg munkát jelent, másrészt nagy mennyiségű mérési hiba halmozódhat fel.

) (n² O

Amint láttuk, Broadbent és Calcott a folyamatos őrlés tanulmányozására megadták a legegyszerűbb modelleket, s elkezdődött a folyamatos őrlés vizsgálata. Mielőtt azonban rátérnénk a folyamatos őrlés tanulmányozására, folytatjuk az újabb szakaszos őrlési modellek ismertetését, mert a szakaszos őrlés most ismertetendő, későbbi, kiforrottabb eredményeit a folyamatos őrlés tanulmányozása során is felhasználják.

A továbbiakban bemutatásra kerülő modellek többségében előfordul a szelekciós függvény, a törési eloszlásfüggvény vagy a törési sűrűségfüggvény. Egyes matematikai leírásokban a szemcseméret szerinti tömeg-eloszlásfüggvény helyett a maradék-

eloszlásfüggvény szerepel. Ezért most ismertetjük ezek definícióit. A törési szelekciós függvény, S(x) kifejezi, hogy egy időegység alatt az x méretű szemcsék hányad része törik el. A törési eloszlásfüggvény, az L méretű szemcse törésekor keletkező törmelék eloszlását adja meg. A törési sűrűségfüggvényt b(x )-lel jelöljük,

megadja az L méretű szemcse törésekor az (x,x+dx) szemcseméret intervallumba tartozó )

, (x L B

,L

sék

min

üggvényét a t időpillanatban M(x,t)- vel jelölve, az R(x,t)=1-M(x,t)-vel definiált függvényt az őrlemény szemcseméret sze

y vélték, hogy a fenti kérdések megválaszolásához –

t az energia

x L x b( , )d

szemc hányadát. E két függvény közötti kapcsolat: ^B(x,L)=

∫

x

ahol x_min jelöli a legkisebb szemcseméretet, vagyis azt a méretet, amelynél kisebbre a szemcse nem törik.

Az őrlemény szemcseméret szerinti tömeg-eloszlásf rinti maradék-eloszlásfüggvényének nevezzük.

Napjainkra az őrlés szaktekintélyévé vált Austin 1964-ben kutatótársával közösen írt tanulmányában (Austin & Klimpel, 1964) kifejtette, mennyire tág az őrlés témaköre. A malmok tervezésekor az alábbi öt kérdés figyelembevételét alapvető követelménynek ítélték: Milyen típusú őrlőgépet válasszanak? Milyen karbantartásra lesz szükség?

Milyen méretű gépre van szükség? Milyen előírások vonatkoznak az őrleményre?

Változó betáplálás esetén milyen lesz a malom teljesítménye és melyek az optimális működési feltételek? A szerzők úg

különösen az utolsóéhoz - az őrlési elmélet kidolgozására van szükség, amelyhez maguk is nagyban hozzájárultak.

Austin és Klimpel ismertették az őrlemény szemcseméret szerinti tömegeloszlását leíró egyenletet, amit elneveztek a szakaszos őrlés alapegyenletének. A szerzők előbb beszámoltak az egyenletben szereplő függvények, a szelekciós függvény – S(x) – és a törési eloszlásfüggvény –B(x,L)– alakjának meghatározására végzett kísérleteikről.

Megállapították, hogy a szelekciós függvény a szemcseméret valahányadik hatványával arányos. A hatványkitevő függ az őrlőkészülék geometriai méreteitől, az őrlés módjától, az őrlendő anyag szerkezetétől. A kutatók szerint nem áll fenn általános érvényű kapcsola bevitel é őrlemény átlagos szemcsemérete között. A szerzők a törési eloszlásfüggvényt vizsgálva kísérleti úton e függvény alakjára az alábbi képletet kapták:

s az

L L x x

B( , )= , ahol B(x,L) az L méretű szemcse törésekor keletkező törmelék eloszlása. Felhasználva e függvényeket, Austin és Klimpel megadták t ideig tartó őrlést követően az őrlemény szemcseméret szerinti tömegeloszlását leíró alábbi egyenletet:

dydt y x B y S y t y M x

M t x

max

) , ( ) ( / ) , ( [ ) 0 , ( ) ,

( ^{= +}

∫ ∫

M

x 0

s ezt a szakaszos őrlés alapegyenletének nevezték, ahol M(x,t) jelöli a t ideig tartó őrlést követően az őrlemény szemcseméret szerinti tömeg-eloszlásfüggvényét, x_max pedig a legnagyobb szemcseméretet, S a szelekciós, B a törési eloszlásfüggvényt. A szerzők a modelljüket véges differencia módszerrel diszkretizálták, s ezt követően IBM 7074 számítógépre írott programmal végeztek numerikus kísérleteket a modelljük igazolására. A tapasztalati úton nyert és a számított eloszlások nagyon közel álltak egymáshoz. A szerzők az analitikus megoldással nem foglalkoztak. A numerikus módszerek alkalmazását helyezték előtérbe, azonban a közelítés pontosságáról nem

nyi

kell tanulmányozni (Reid, 1965). A szerző a pusztán kísérleti eredményekre támaszkodó modellek alkalmazását kétségesnek tartotta a bennük elkerülhetetlenül előforduló mérési hibák miatt. Reid az őrlés alapegyenletét az alá i formában írta fel:

latkoztak, megelégedtek azzal, hogy a numerikus kísérleti eredményeik jól megközelítették a tapasztalati eredményeiket. A kutatók az őrlés tanulmányozására szorgalmazták a számítógép használatát, amelyre példát is mutattak.

Reid 1965-ben az addigi publikációk tanulmányozásából arra a következtetésre jutott, hogy a szakaszos őrlést lehetőleg az őrlési alapegyenlet analitikus megoldásával

bb x dL

t L L M

x k L x B x

t x x M t k

x t x M

x ∂

⋅∂

∂ ⋅ + ∂

∂

− ∂

∂ =

∂

∂ ^{( , ) ( ) ( , ) max}

∫

ahol M(x,t) jelöli a tömeg-eloszlásfüggvényt, B(x,L) a törési eloszlás szelekciós függvényt, x a legnagyobb szemcseméretet, x a szemcse

Az alapegyenletnek ezt a formáját többen is használták, azonban bizonyára kényelmi

2 x

függvényt, k(x) a méretet, t az időt.

max

okokból áttértek a tömeg-sűrűségfüggvényre, s erre általában az

x t x t M

x

m ∂

∂ ( , )

= ) ,

(

jelölést vezették be. A szelekciós függvényt pedig gyakran a nevére is utaló S(x) függvénnyel jelölték k(x) helyett.

A szerző megadta a megoldásokat abban a speciális esetben, amikor k(x)=k·x és L

L x x

B( , )= . Azokban az esetekben, amikor az analitikus megoldás nem ismert, Reid

alkot paramé

az i-dik frakcióba törő szemcsék tömeghányadát (ahol

< -1, ahol n a szemcseméret osztályok szám =1 jelöli a legnagyobb szem tömeghányadok tapasztalati úton megállapítha- véges differencia módszerrel történő diszkretizálás után közelítő megoldás előállítását javasolta rekurzió alkalmazásával. A közelítő megoldás kiszámítását a szerző számító- gépes programmal végezte. Reid egy olyan szemcseméret és idő szerint folytonos modellt ott, amelyre sokan hivatkoztak, napjainkban is használják.

Reid megadott a megoldásával együtt egy „gyakorlati egyenlet”-nek nevezett méret szerint diszkrét, idő szerint folytonos modellt is, amely tapasztalat útján meghatározható

tereken alapul.

Jelölje )w_i(t az i-dik szemcseméret-osztályba tartozó szemcsék tömegének arányát, rövidebben az i-dik frakció tömeghányadát at-dik időpillanatban, jelölje b_i,j egy rövid őrlési idő alatt a j-dik frakcióból

j

i x , i>j, j=1,2,…,n

csék osztályát). A

a és j

j

bi_,

x

tók. Az i-dik frakció törési hányadát jelölje k_i. A bevezetett jelölésekkel Reid az alábbi

„gyakorlati egyenlet”-et írta fel:

) ( )

dt _{j 1} ^{i,j j j}( ^{i i} )

( dw_i t ^{i 1}

t w k t w k

∑

=

−

= (i=1,…,n),

ahol n a szemcseméret-osztályok száma. A legnagyobb szemcsék osztályára i= 1 , míg a legkisebbekére i=n. A „gyakorlati egyenlet”-et később mátrix alakban is felírták, s abban a formában is nagyon használhatónak bizonyult – mutatott rá később Berthiaux (Berthiaux et al., 1996a).

Az őrléssel kapcsolatos publikációk feldolgozásában, rendszerezésében, az őrlési ismeretek fejlesztésében kiemelkedő tevékenységet végzett Beke Béla, aki az őrlés fő kérdéseiről adott áttekintést gyakorló technológus mérnököknek szánt monográfiájában (Beke, 1963). Beke könyve alapmű, ilyen áttekintő munka sem a hazai, sem a külföldi szakirodalomban korábban nem állt rendelkezésre. A szerző egy-egy fejezetben foglalkozik az őrlemény szemcseösszetételével, az aprítási folyamatok energia- igényével, az aprítás kinetikájával, ismerteti a körfolyamatos őrlés elméletét, és annak hatását az őrlemény szemcseméret szerinti összetételére.

Az őrlemény eloszlása vizsgálata során az 1960-as évekre kiderült, hogy Brown előrejelzése bevált, mert az őrlemény Rosin-Rammler-eloszlása ellenőrzésére a köztudatba kerülése óta a hatvanas évekig vizsgálatok ezreit végezték el – írja Beke (Beke, 1963) –, és megállapították, hogy finomőrlésnél a mikroszkópos nagyságrend felett statisztikai érvényessége elfogadható pontosságú. Többen – köztük Bennett, Romadin, Sperling – próbálkoztak az eloszlás elméleti levezetésével, azonban min

egmutatták, hogy a szelekciós függvény és a törési sűrűségfüggvény spe

Az egy

oglalta az addigi modellekben alkalmazott fogalmakat, megadta ezek pontos jelentését és jelölését, a különböző formában felírt mo

t kísérleti cé kü

gyenletének a ha n sá

lásfüggvény speciális megválasztásai esetén, amikor a szelekciós gg

degyik levezetés tartalmaz önkényes feltételezéseket. Mintegy harminc évvel kés- őbb, 1996-ban Mihálykó Csaba és Blickle Tibor a szakaszos őrlés matematikai modellezése során szintén vizsgálták az őrlemény eloszlását (Mihálykó & Blickle, 1996). A szerzők m

ciális megválasztása esetén, ha a kezdeti eloszlás a Rosin-Rammler-eloszlással jellemezhető, akkor az őrlés minden időpillanatában az őrlemény időtől függő paraméterű Rosin-Rammler-eloszlású lesz. A Rosin-Rammler-eloszlás használatának elterjedése az eloszlás jó kezelhetőségére is visszavezethető.

Az 1970-es évekre már az őrlés leírására szolgáló sok modellben fordult elő a törési eloszlásfüggvény – állapították meg Austin és Luckie (Austin & Luckie, 1971/72). A szerzők a diszkrét törési eloszlásfüggvény általuk kidolgozott meghatározási módszerét is ismertették.

Ezekre az évekre lehetővé vált a malom működésének elfogadható pontosságú szimulációja, legalábbis a kisméretű kísérleti malmok esetén (Austin, 1971/72).

mástól független kutatócsoportok jelölései, matematikai technikái különbözőségei miatt azonban a modellek közötti kommunikáció nagy akadályokba ütközött, ezért Austin megtette az első lépéseket az egységes jelölésrendszer bevezetésére. A szerző egy áttekintést publikált, amelyben összef

delleket átírta az egységes jelöléseknek megfelelően.

A Rosin-Rammler-eloszlás használata mellett a kutatók az őrlemény eloszlását vagy kísérletek útján állapították meg, vagy a modelljeik alkalmazásával számították ki.

A főkén lú malmok működésének sikeres szimulálása után a kutatások a lönféle típusú és célú ipari és laboratóriumi őrlőkészülékek modellezésére, a segéd- függvények meghatározására irányultak, az alkalmazott matematikai eszközök széles skálájának igénybevételével.

Gupta és Kapur cikkükben (Gupta & Kapur, 1975) megadták a szakaszos őrlés tömeg-sűrűségfüggvényre felírt alape so ló gi megoldását a szelekciós függvény és az elosz

vény S(x)=k⋅x^α, ahol x jelöli a szemcseméretet, k>0, α>0, az eloszlásfüggvény fü

⎞β

=⎛x L x

B( , ) _⎟ , amely az L méretű szemcse törésekor keletkező törmeléke

⎜ ⎠

⎝L k eloszlása,

l β>0. Ilyen feltételek mellett a hasonlósági me oldás egy általánosított gamma gvény az α=β választása a R er-elo

aho g

füg α=1 esetben, osin-Ramml szlást eredményezi. A

szerzők pszeudo-hasonlósági megoldást is megadtak a szelekciós és az eloszlás-

β

függvények sokkal általánosabb osztályára, ahol S(x)=k⋅[φ(x)]^α,

φ φ ⎟⎟⎠

⎜⎜ ⎞

⎝

=⎛ ) (

) ) (

,

( L

L x x

B ,

φ tetszőleges monoton nem-csökkenő függvény.

Fan és Srivastava idő szerint folytonos, szemcseméret szerint diszkrét sztochasz- tikus modellt fejlesztettek ki (Fan & Srivastava, 1980). Feltételezték, hogy

1) annak a valószínűsége, hogy a szemcse az i-dik állapotból – ami az i-dik szemcseméret- intervallumba tartozást jelenti – ∆t idő alatt az (i-1)-dik állap ba kerül, )_i t o(∆t

ot +

∆

λ ⋅ , ahol λ_i konstans, és o(∆t)/∆t →0, ha ∆t →0, továbbá 2) az i-dik állapotból valamely (i-j)-dik állapotba – ahol >1 – kerülés valószínűsége j

∆t idő alatt o(∆t).

A szerzők megadták a szemcsék szétesési folyamata során a szemcsék méret szerinti eloszlását, megadták az egyes szemcseméret-osztályokba tartozó szemcsék várható értékének és szórásának kiszámítási képleteit, amelyekkel az őrlési folyamat bármelyik pillanatában megkapjuk ezeket az értékeket. Végül Fan és Srivastava megadták az egyes osztályokba tartozó anyagmennyiségek kiszámítási képletét is. A modell alkalmazása egyszerűnek látszik, viszonylag kevés paramétert kell mérésekkel becsülni.

A szerzők azonban nem indokolták publikációjukban, miért helytállóak a fenti feltevéseik, melyeket a levezetések során kihasználtak. A kutatók csupán a λ_i-k kiszámítására mutattak példát abban az esetben, amikor a szemcseméret-osztályok száma 5 volt.

A szakaszos őrlést véletlentől függő folyamatként vizsgálta Verdes Sándor (Verdes, 1984). Az őrlés különböző időpontjaihoz tartozó őrlemény-eloszlások momentumainak időbeli változását írta le. A szerző célja az volt, hogy modelljével több őrlemény- jellemző változása legyen egyidejűleg nyomon követhető. Verdes a modelljében szerep- lő paramétereket kísérleti mérés-sorozatokkal határozta meg, majd modellje igazolására laboratóriumi golyósmalmi őrlési kísérletekkel végzett ellenőrzéseket. A tapasztalati úton nyert és a modell alkalmazásával számított eredmények nagymértékben egyeztek.

Nakajima és Tanaka kísérleteket végeztek a szelekciós függvény és az eloszlás- függvény szorzatának közelítésére. Majd ezt követően a szakaszos őrlés egyenletének az őrlemény szemcseméret szerinti maradék-eloszlásfüggvényével, R(x,t)-vel felírt alakjából kiindulva Laplace-traszformáció alkalmazásával analitikus megoldást adtak meg a szerzők (Nakajima & Tanaka, 1973). (A törés előtti szemcseméretet L, a törés utánit x, az időt t jelöli.) A függvények szorzatára az alábbi képletet használták:

β α ⋅⎜⎛ ⎟⎞

⋅ x

x

k , ahol k konstans, az α, β konstansok értékei az 1 közelében vannak. A

⎠

⎝L

szerzők őrlési kísérleteket végeztek modelljük igazolására. Az α, β értékeire vonatkozó előírások erősen leszűkítik a modell alkalmazási területét.

Később, Nakajimához és Tanakához hasonlóan 1992-ben Gurevich, Kremer és Fidlin az őrlési egyenletet az őrlemény szemcseméret szerinti maradék-eloszlás- függvényével írták fel és feltételezték, hogy a szemcsék szétesésekor a törmelék elosz- lása a Goden-Schulmann-Andreev egyenlettel írható le (Gurevich et al., 1992).

Nakajima és Tanaka módszeréhez hasonlóan a szerzők az analitikus megoldást Laplace- traszformáció alkalmazásával kapták. Végül a kutatók összehasonlították a számított és a tapasztalati eredményeket, s megállapították, hogy ezek nagyon közel állnak egy- máshoz. Bár Gurevich és kutatótársai munkája – a Goden-Schulmann-Andreev egyen-

lete

eplő törési eloszlásfüggvénnyel azonos, a szelekciós függvénnyel k=1 esetén megegyező függvényeket tekintve László Zoltán olyan szakaszos őrlésre vonatkozó modelleket ismertetett publikációjában, amelyek megoldása zárt, vagy egy jól számolható végtelen függvénysor alakjában felírható (László, 1993). László kitért a szelekciós és a törési eloszlásfüggvény paramé-

rei különböző megválasztásával előálló me azt is vizsgálta, hogy léletet, amely szerint a természet folyamatait jól leíró matematikai t kivéve – nem sokban tér el Nakajima és Tanaka munkájától, megerősíti Nakajima és Tanaka módszere és a Laplace-transzformáció alkalmazhatóságát az őrlés kutatására.

Gupta és Kapur 1975-ben közölt fenti cikkében szer

te goldásokra, és

különböző kezdőfeltételek esetén hogyan állítható elő a megoldás. A szerző az egzisz- tencia kérdésének vizsgálatával cikkében nem foglalkozott. E helyett elfogadta azt az alkalmazói szem

modell megoldható, hiszen a valóságban megjelenik a megoldás.

Mihálykó Csaba dolgozatában a szakaszos őrlésnek a sűrűségfüggvényre vonatkozó integro-differenciálegyenletének megoldásával foglalkozott (Mihálykó, 1995a). Az alapegyenletnek a szerző által közölt formája az alábbi:

∫

+

−

∂ = ^m

) , ( ) , ( ) ( ) , ( )

( ( ^x

x

dL t L m L x b L S t

x m x x S

m ,

ahol x_maxa legnagyobb szemcseméretet jelöli, b(x,L) a törési sűrűségfüggvény, m(x,t) a malomban tartózkodó anyag méret szerinti tömeg sűrűségfüggvénye az x méretnél a t időpillanatban.

∂ ) ax

, t

t

A szerző igazolta, hogy bizonyos feltételek mellett létezik a fenti integro-differenciál- egyenletnek megoldása és a megoldás egyértelmű. Mihálykó megadta a megoldás sor alakját és a simaságra vonatkozóan néhány tulajdonságát, s azt is megmutatta, hogy a fizikai háttérből származó néhány természetes elvárásnak is eleget tesz a megoldás.

Azaz, a megoldás valóban sűrűségfüggvény, és megfelel annak a kívánalomnak, hogy rögzített ]x∈]x_min,x_max esetén lim ( , )=0

∞

→ m x t

t teljesüljön, ami azt fejezi ki, hogy leőrlődik az anyag, ahol x_min azt a méretet jelöli, amelynél kisebbé a szemcse nem törhet. A szerző vizsgálta a megoldás aszimptotikus viselkedését és néhány esetben analitikus megoldást is megadott. Az egyenletet numerikusan is megoldotta a szerző, explicit és implicit módszerek alkalmazásával egyaránt. Megvizsgálta a kutató az alkal- mazott numerikus módszerek stabilitását, konvergenciáját, valamint azt, hogy milyen feltételek mellett őrzik meg a kapott közelítő megoldások a folytonos modell kvalitatív tulajdonságait.

Végül a kutató összehasonlította az analitikus megoldásokat a numerikus módszerek alkalmazásával kapott közelítő megoldásokkal. Ezek nagymértékű egyezését tapasztalta a szerző. Mihálykó egy másik munkájában (Mihálykó, 1995b) bizonyos feltételek teljesülése esetén az alapegyenlet megoldását vizsgálta a korlátos és szakaszonként folytonosan differenciálható függvények, továbbá a kétszer folytonosan differenciálható függvények körében. A speciális kvadratúra formulák alkalmazásával konstruált diszkrét közelítések kielégítik a nemnegativitást és a diszkrét megmaradási törvényt, az egzakt megoldás másodrendű közelítését adják.

Később Stoyan, Mihálykó és Ulbert a szakaszos őrlés integro-differenciál- egyenletének megoldását Szoboljev–terekben vizsgálták (Stoyan et al., 1998). Mivel az általános megoldás nem adható meg, a szerzők közelítő megoldást konstruáltak a Galerkin-féle végeselem módszer alkalmazásával. A szerzők foglalkoztak a stabilitás, konvergencia, anyagmegmaradás, nemnegativitás kérdésével. Elegendően sima függvé-

nye

A szakaszos őrlés alapegyenlete megoldására egy numerikus eljárást, a harmad- almazásának módszerét ismertették

al., 1997). U a hasonlósági egyenlet megoldására is

a

kre a numerikus megoldások az egzakt megoldások magas rendű közelítéseit adják.

Ezután a numerikus és az elméleti megoldás összehasonlítását végezték el a kutatók a szelekciós és a törési eloszlásfüggvény néhány esetében. Csekély eltérések mutatkoztak az elméleti és a numerikus úton kapott eredmények között.

rendű splineok alk Everson és kollégái (Everson et

gyanez a megközelítés alkalmazható

bban az esetben, amikor a törési eloszlásfüggvény sokkal bonyolultabb formájú annál, hogy az analitikus megoldás ismert legyen. A hasonlósági egyenletek esetén a spline együtthatók egy sajátérték probléma megoldásával kaphatók meg. A szerzők a közölt módszerükkel kapott numerikus megoldást összehasonlították egyrészt az analitikus megoldással néhány speciális esetben, másrészt a mészkő és aranyérc őrlése során nyert tapasztalati eredményeikkel. A spline módszer alkalmazásával számított eredmények nagyon jól megközelítették a tapasztalati eredményeket.

Austin megmutatta, hogy tipikus esetekben a szakaszos őrlés integro-differenciál- egyenletének megoldása csaknem teljesen megegyezik a szakaszos őrlés méret szerint diszkrét és idő szerint folytonos – Reid által megadott (Reid, 1965) – modelljének megoldásával (Austin, 1999). A szerző a szelekciós függvényt S(x)=k⋅x^α, míg a törési el szlásfügg

β γ

o vényt Φ Φ _⎟

⎜ ⎠

⋅⎝

−

⎟ +

⎜ ⎠

⋅⎝

= L L

L x

B( , ) (1 ) alakban vette fel, ahol k, α, onstans k, x és L jelöli a szemcseméretet.

A méretcsökkentésnek, az ő őrlési alapegyenlettel történő le ás

alkalmazzák ezt a leírásmódot – állapították meg az utóbbi idők idevonatkozó publikációi felsorolásával Kostoglou és Karabelas (Kostoglou & Karabelas, 2002). Az őrlési alapegyenlet megoldása azonban egyáltalán nem triviális, ezért igen sokféle megoldási módszert javasoltak. A numerikus megoldások közül a szerzők kiemelték a diszkretizáció

⎞

⎛

⎞

⎛x x

β, γ, Φ k o

rlésnek a populációs mérlegegyenlettel, különösen az ír a széleskörűen elterjedt, s napjainkban is sokan

módszerét, mint a legfontosabb módszert. A szerzők további módszerek mlítése után rátértek an

e nak vizsgálatára, hogy a gamma eloszlás mennyire jól írja le az őrlemény eloszlását. Kostoglou és Karabelas a korábbiak során már többek által használt momentumok módszerét alkalmazták. A szerzők összehasonlították az anali- tikus és a közelítő megoldásokat azokban a speciális esetekben, amikor az egzakt meg- oldás is megadható.

Jelölje τ az időt, x a szemcse tömegét, f'(x,'τ) a szemcseszám szerinti sűrűség- függvényt, p'(x ,'y') az y' tömegű szemcsék törésekor keletkező 'x tömegű szemcsék valószínűségeloszlását. Legyen f₀^'(x')= f'(x,'0), M ^=∞

∫

0

0'( )dx, ⁼

∫

0 0 0 f '(x)dx N

0

0 N

x = M . A p(x,y)= p'(x,'y')/x₀képlettel definiált függvényt törési magnak nevezzük. A szerzők bemutattak olyan törési mag választást, amikor az analitikus és a közelítő megoldás kevéssé tért el egymástól. Így a szerzők az őrlemény eloszlásának egy kevésbé elterjedt megállapítási módjára hívták fel a figyelmet.

A matematikai leírásokban fontos szerepe van a szelekciós és a törési eloszlás- vagy törési sűrűségfüggvénynek. E függvények meghatározásával számos publikáció foglalkozik, közülük csak a legfontosabbakat ismertetjük.

Az egyes méretosztályokba tartozó szemcsék törését számos kutató vizsgálta nyomjelző anyagok használatával (Gaudin et al., 1951, Moore, 1964, Kelsall, 1964).

Kelsall golyósmalmi őrlési kísérletei során nyomjelzőként kvarcot alkalmazva megállapította, hogy a törési eloszlásfüggvény az alábbi alakú (Kelsall, 1964):

n

L L x x

B ⎟

⎠

⎜ ⎞

⎝

=⎛ ) ,

( , ahol 0,90≤n≤0,95.

Berthiaux és kutatótársa 1996-ben bemutattak egy m ert e függvények közelítő kiszámítására (Berthiaux et al., 1996a). A szerzők Reid – (Reid, 1965) – mátrix alakban felírt „gyakorlati egyenlet”-éből kiindulva az i-dik szemcseméret osztályba tartozó szemcsék törési hányadát k_i helyett S_i-vel jelölve, az alábbi mátrixegyenletet tekintették:

i ódsz

) ( )

( )

d ( ) (

d B I S W t A W t

t t

W = − ⋅ ⋅ = ⋅ ,

ahol W(t) oszlopvektor, melynek i-dik komponense w_i(t) az i-dik szemcseméret- osztályba tartozó szemcsék tömeghányada a t-dik időpillanatban. Az egyenletben szereplő B mátrix alulról trianguláris mátrix, ahol B(i,j)=b_i,j egy rövid ideig tartó őrlés alatt a j-dik frakcióból az i-dik frakcióba törő szemcsék tömeghányadát adja meg. Az S diagonális mátrix, melyet a kutatók elneveztek szelekciós mátrixnak, mert a fődiagonálisában a szemcseméret-osztályokra vonatkozó törési hányadok állnak, azaz S(i,i)=S_i. Az A mátrix időtől való függetlenségét feltételezve a szerzők egy egyenletrendszert kaptak w_i(t)-re (i=1,…,n), amelyből )R_i(t -re vonatkozó egyenlet- rendszerre tértek át, ahol R_i(t) az 1-től i-ig terjedő méret-intervallumokba tartozó szemcsék maradék-eloszlásfüggvénye. (A legnagyobb szemcsékre i=1.) A szerzők a B mátrix, a törési mátrix elemeit a szelekciós mátrix elemeivel fejezték ki. Ehhez a Kapur- féle approximációs formula (Kapur, 1970) Berthiaux-féle általánosított alakját használták. Így a megoldáshoz elegendő a szelekciós mátrix (vagy a szelekciós függvény) ismerete.

Az őrlés kezdeti időszakára – 15 perc vagy annál kevesebb – korlátozva a vizsgálódást, a sz

őrlésre is – írják a szerzők. Szerintük a módszer azonban nem

izonyára ez is az egyik oka lehet – a kutatók által megadott alkalmazhatósági korlátokon kívül –, hogy a törési mátrixnak a ciós mátrix elemeiből történő kiszámítása nem terjedt el, e módszer használata erthiaux kutatócsoportjához kapcsolódik.

ételten felhívták a elmét a Kapur-féle – (Kapur, 1970) – approxi- ációs formula használatára az őrlemény maradék eloszlása meghatározására (Be

erzők megmutatták, hogy az S (és a B) mátrix a szakaszos őrlési tesztekből meghatá- rozhatók (anélkül, hogy bármilyen feltevéssel élnénk a szelekciós és a törési sűrűségfüggvény matematikai alakjára vonatkozóan). Ez a módszer kiterjeszthető rövid tartózkodási idejű folyamatos

alkalmazható hosszabb tartózkodási idő esetén és akkor sem, amikor az őrlésnél különféle hatásokat kell figyelembe venni, például a belső osztályozást vagy a pép áramlása során bekövetkező változásokat. A kutatók laboratóriumi őrlési kísérletekkel illusztrálták e közelítő kiszámítási mód gyakorlati alkalmazhatóságát.

Az ismertetett matematikai levezetésből kiderül, hogy Berthiaux és munkatársai azzal a feltevéssel éltek, hogy a szemcse törés hatására másik méret-intervallumba kerül. Ehhez azonban, figyelembe véve mindazokat a töréseket is, amikor a szemcséről kicsiny részek „pattannak le”, a szemcseméret-intervallumok számát rendkívül nagyra kellene választani, a szelekciós mátrix meghatározása pedig nagyon nagy pontosságú méréseket igényelne. E tényeket a szerzők nem említették. B

szelek B

Később, 1999-ben Berthiaux és Dodds egy újabb cikkben ism gyakorlati szakemberek, mérnökök figy

m

rthiaux & Dodds, 1999).