Angular Momentum of Multispin

C H A P T E R 4

Angular Momentum of Multispin Systems

1. Products of Vector Spaces A. Introduction

T h e greater part of the theory of angular momentum developed in Chapter 2 was restricted to the case for which the eigenvalues of I^z were nondegenerate, and thereby limited to systems consisting of a single particle with spin quantum number / . This limitation is much too severe for later problems, which will be almost exclusively concerned with systems consisting of several spinning particles, occasionally even with systems composed of an arbitrary number of such particles. It is necessary, therefore, to generalize the single-particle theory of spin angular momentum to include multispin systems.

T o fix ideas, let Ι^χ and I² denote two noninteracting spin angular momenta with I¹ = \ and I² = 1. An arbitrary state of the first particle can be represented by a normalized vector in a two-dimensional spin space:

1 0 = a

l/2

2

-l/2

2

An arbitrary state of the second particle is represented by a normalized vector in a three-dimensional spin space:

| 2 > = Α¹| 1 , 1 > + * ο Ι 1 , 0> + 6_1| 1 , - 1 > .

Since the particles do not interact, a state of the composite spin system is defined whenever the states of its component systems are specified.

Hence a generic state of the joint system is described by a vector pair such as [I 1>, I 2>]. Specifically, if both particles are quantized in the ζ direction, the combined system will be defined by one of the six vector

95

96 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S

couples: [| \, -|>, | 1, 1>], [| \ , -|>, | 1, 0>], which correspond to total ζ components of angular momentum m = m¹ m² = F > I > — È > È >

_ 1 _ 3 2 > 2 ·

For a single particle with spin 7, the total number of m values (i.e., 21 + 1) is equal to the dimension of the spin space, and the associated eigenvectors form a basis for this space. If it is assumed that these properties also hold for a composite spin system, it follows that the composite spin space is six-dimensional, and that the vector pairs which generate the six possible values oi m = m¹ -\- m² constitute a basis for this space. On this assumption, a generic state [| 1>, | 2>] may be ex- pressed

[I 1>, I 2>] = £ £ c^mini2 [I 7^X , <>, 11², m²}l

where, in terms of the notation introduced above,

This equality must hold if the expansion is to include the six vector pairs {[| Ix , w^x>, 112 , m²>]} as special cases. For example, the pair [|£, — |->, I 1, 0>] is specified by the relations a_^1/2 = e^ioLy b^Q = e~^ioLy

ai/2 = hi = b_^x = 0, so that all c^mi)n are zero except ^_ι/²,ο ^{= α}-ι/2^ο >

whose value is unity.

T h e preceding example does not provide a rigorous definition of the vector space required for the description of a composite spin system, but it does reveal some characteristic properties of this space. In particular, it shows that vectors in the composite spin space are con- structed from vectors of the component spaces, and that the dimension of the composite space is equal to the product of the dimensions of the component spaces. These properties are characteristic of a product space, which will now be formally defined.

B. Definition of Product Spaces

Let S^± and *S² be finite-dimensional unitary vector spaces with dim S¹ = m and dim S² = n. With every vector χ in S¹ and every vector y in S² , one can associate an ordered vector pair¹ χ (x) y called the product of χ and y. T h e vector χ (X) y is an element in a new vector space, called the product space of S1 and S2 , defined as the

1 H e n c e f o r t h , the o r d e r e d vector pair [x, y] will be d e n o t e d χ (X) y.

1 . P R O D U C T S O F V E C T O R S P A C E S 97

set of all linear combinations of all ordered pairs χ (χ) y with the properties

(x¹ + x²) ®y = (x)y + x² ®y, (1.1)

*®Cvi +^

) =

c(x ® y) = (cx) (x)y = χ ® (cy), (1.3)

(Λ?! ® y¹ , *2 ® J >2) = (x¹ ,

x

)(^i

Equations (1.1) through (1.4) provide the fundamental rules for the manipulation of ordered pairs χ ® y. With these rules of operation, one can show that the set S satisfies all the axioms in the definition of a vector space (7, 2).

Let {e1, e^m} and {fx, . . . , /n} be orthonormal bases for S1 and S2 . If # and y are vectors in S± and AS² , then

x

= X ' ^

X

and, by (1.1) through (1.3),

χ ®y = ΧΧ &^Α· ®Λ · (1-5)

T h u s any ordered pair Λ; ® J; may be expressed as a linear combination of the tnn pairs eⁱ ®f^{r 9} so that these elements span S. Moreover, these vectors are independent, for if

i,r

then the scalar product of this equation with e$ ® /s gives X <Vr(*i ® Λ » ® Λ) = X *fr δ,?· 5^{< sr} = C js = 0,

i,r i,r

by (1.4) and the assumed orthonormality of the e's a n d / ' s . T h u s the set {eⁱ ® f^r} is a basis for S, so that

dim S = dim £χ dim S2 .

T h e basis {eⁱ ® /^r} will be referred to as the product basis.

T h e product space of a finite number of finite-dimensional vector spaces S1 , £² , S^N is defined as follows. One first forms S1 ® S² ,

98 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S

then ( S i ® S2) ® S³ ···, and, finally, {(S1 ® S²) ® ···} ® S^{N )} which is abbreviated²

5 is spanned by the set of all linear combinations of all ordered vector TV-tuples X-^ (x) X2 ' ' ' ® xN , where each xi is a vector in St . These iV-tuples satisfy relations analogous to (1.1) through (1.4), and one can show that if { e j , { / J , {^J, ... are bases for S¹, S², then {ei ® / j ® g h. ® ***} i^{s a} basis for S ; hence

dim S = dim .Sx dim S2 ··· dim .S^ . (1.6) If the vector spaces Sx , 52 , ... are spin spaces for particles with spin

quantum numbers Ix, I² , then, since dim 5^ = 2 /{ + 1, the dimen- sion of the product spin space is

d i m S = n(2// + l)- (1.7)

2 . Kronecker Products of Linear Transformations A. Definition of Kronecker Products

T h e completion of the mathematical basis for the theory of multispin systems requires only the concept of a Kronecker product of linear transformations. This concept provides the means for converting linear transformations defined on the component spaces into linear trans- formations on their product space.

T h e necessity for introducing the Kronecker product of linear transformations can be easily appreciated by considering the example discussed in the preceding section. If both spins are quantized in the ζ direction, the components of the total angular momentum along the ζ axis are given by f , J , J , — J , — J , — f . T h e question which immediately arises is: What operator is associated with these eigen- values ? Since the values of the total spin variable are obtained by sum- ming the component spin variables, it seems natural to assume that the operator for the ζ component of the total angular momentum is

Iz = Izi H~ I^Z2

-

2 T h e o r d e r in w h i c h the vector spaces .St are c o m p o u n d e d to form their p r o d u c t space S is arbitrary, b u t once a definite o r d e r has b e e n settled u p o n , it m u s t be m a i n t a i n e d . T w o p r o d u c t spaces w h i c h differ only in t h e o r d e r in w h i c h their c o m p o n e n t spaces have been multiplied are related by a p e r m u t a t i o n t r a n s f o r m a t i o n .

2. K R O N E C K E R P R O D U C T S O F L I N E A R T R A N S F O R M A T I O N S 99

This assumption is not correct; for if Izl and Iz2 are represented by matrices, the right side of this equation will be represented by

This result is absurd. Not only is the sum of these matrices undefined, neither matrix is the representative of an operator defined on a six- dimensional space. These difficulties are removed by the Kronecker product of linear transformations.

Let A and A' denote arbitrary linear transformations of S1 into itself, and lx the identity transformation on S1 . Similarly, let Β and B' denote arbitrary linear transformations of S2 into itself, and 12 the identity transformation on S2. If χ and y denote arbitrary vectors in Sx and S2 , respectively, then x' = Ax and y' = By are also vectors in these spaces.

Thus when 5^X and S2 are subjected to the transformations A and B, the product χ ® y is transformed into Ax ® By = x' ®y'. It follows that the linear transformations A and Β together define a linear trans- formation on S = Sx ® S2 . This transformation, called the Kronecker product of A and B, is denoted Α ® Β and is defined by the equation

(A ® B)x ®y = Ax® By. (2.1)

From this definition, one can deduce a number of important properties of the transformation A ® B.

Consider first the case where A = lx and Β — 12 . Since 1λχ = χ and l2y = yf it follows that 1λ ® 12 is the identity operator for S. On the other hand, if Β = 12, but Α Φ lx, then

(A ® J²)x ®y = Ax®l²y = Ax®y. (2.2)

This equation shows that the operator A ® 12 transforms the com- ponents of a vector in S but has no effect on the S2 components. A similar remark applies to the operator lx ® B, since

(7x ® B)x ®y = llX®By = x® By. (2.3) Equations (2.2) and (2.3) provide the rules for converting operators

defined on the component spaces into operators on the product space.

T h e prescription is simple: A —>- A ® 12 , Β —> lx ® B. Thus the answer to the question previously posed is I^z = I^zl ® 1² + 1± ® I^Z2 >

and it will be shown below that this formula removes all the dimen- sionality problems encountered with the incorrect expression Izl + Iz2 .

100 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S

Consider now the Kronecker product A' ® B' and apply this operator to both sides of (2.1). Since χ and y are arbitrary, one obtains

(Α' ® B')(A ®B) = Α'A ® B'B. (2.4)

This equation states that the (ordinary) operator product of two Kronecker products is equal to the Kronecker product of the (ordinary) operator products. The order of the factors on both sides of (2.4) is important, since the operators A, A' or B, B' may not commute. Indeed, if the primed and unprimed quantities in (2.4) are interchanged, one concludes that [A' ® B\ A ® B] = 0 if and only if [Α, Α'] = [Β, B'] = 0.

Since 11 commutes with every A, and 12 commutes with every B, it follows that

(A ® l2)(lx ®B) = (I, ® B)(A ®12) = A®B. (2.5) Hence operators defined with respect to distinct component spaces

commute when interpreted as operators on the product spaces. Equation (2.5) is thus the mathematical expression of the quantum mechanical statement that operators referring to independent particles commute.

If A and Β have inverses, then (2.4) with A' = Α~λ and Β' = Β~λ

shows that

(Α ®B)~1 = A~l®B-\ (2.6)

In particular, if A and Β are unitary, so that A~l =-- A^f and B'1 = B^f, then (2.6) can be written in the form

(A ®By = A' ®B\ (2.7)

It will be shown in Section 2.Β that (2.7) gives the general rule for determining the adjoint of A ® B. Hence A ® Β is unitary or hermitian if and only if A and Β are both unitary or hermitian.

The generalization of the preceding results presents no difficulties.

If C, Z), ... denote linear transformations on Ss , 54 , the Kronecker product A ® Β ® C ® ··· is defined by

(A ® Β ® C ® ·••)(*! ® x2 ® x3 ® ···) = Axx ® Bx2 ® Cx3 ® ··· , where xi is a vector in S{ . The component operators A, B, C, ... are converted into operators on the product space Sx ® S2 ® 53 ® ···

through the prescriptions

A->A®l²®l³-®l^Ny B-+U&B® /2- ® 1N, /x® /2® C - - - ® 7^,...,

and it is easily verified that these operators commute.

2. KRONECKER PRODUCTS OF LINEAR TRANSFORMATIONS 101

Finally, (2.4), (2.6), and (2.7) generalize to

(Α' ®Β' ®C ® -)(Α ®B®C® ···) = ΑΆ ® Β'Β ® CC ® ···, (Α

(χ)

(χ)

(χ)

B. Matrix Representations of Kronecker Products

T h e Kronecker product A ® Β can be represented by a matrix constructed from the matrices representing the operators A and B. T h e matrices of A and Β are defined by their effect on the bases {^}, { /;} of the component spaces:

Ae^r = 2) Alre^l, Bf^s = ^ B^QSf^Q ,

l Q

where /, r = 1, 2, m; q, s = 1 , 2 , . . . , « . It is necessary, however, to introduce an ordering convention for the elements of the product basis {eⁱ ®fj}- T h e customary procedure is the so-called lexicographical ordering, defined by the prescription

{*/ ®fi) = Ul ® / L > el ® Λ > · · · > el ®fn , *2 ® / L ,

e^{2 ® /2 > - M} *2 ® / N » - > *ro ® / L , *ro ® /² > ··>

*ηι

Operating with A ® Β on the r, s element of this basis gives (A ® B)e^r ®/, = Ae^r ® Bf^H =

£ Χ

^{®Λ ·}

I

Q

Taking the scalar product of this equation with ei ® fj gives, by virtue of (1.4) and the orthonormality of the component bases,

(*, ®fj yA®Ber ®/,) = ^ £ AlrBQS(e7., el)(fJ Jq)

l Q

— 2^ ^ AlrB^Qß^?l8j^Q = A^irBj^S.

I Q

T h e scalar product (ei ® fj, A ® Ber ®fs) will be denoted (A ® B)iJ;rit, so that the matrix elements of A ® Β are given by

(A®B)^iJ:r8 = A^irB^ja. (2.8)

102 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S

Equation (2.8) shows that the rows of Α ® Β are labeled with row indices of A and B. One speaks of the "11 row" (read "one-one row"), the "12 row," etc. T o compute the 12 row, one sets i = 1,7 = 2, and then allows r and s to take on all values in their respective ranges, taking care to order these indices lexicographically, as previously noted for the product basis. Similar remarks hold for the columns of Α ® B, so that the full matrix has the form

M A

A\\B^nl

^ 2 1 ^ 1 1

A\\Bn2 - A²¹B¹² -

AⁿBⁿⁿ A²¹B^ln

A¹²B^nl A²²B^U

A\²Bⁿ² A²²B¹²

A¹²Bⁿⁿ A²²B^ln

• A R

A^2mB^ln A²\B^nl A2iBn2 A²¹Bⁿⁿ A²²B^nl A²²Bⁿ² A22Bnn • A R

11

2m

nn

A^m\B^xx A^miB¹² A^mlB^ln A^m2B^xx Am2B12 Am2Bln • A R

\^A^mlB^nl A^m\B^{n2 " A R} Am2Bnl Am2Bn2 - A R

-

m2

-

nn

J

This matrix is called the Kronecker product of A and B\ its form suggests the following simple procedure for writing down the matrix of Α ® Β from the matrices for A and B. Form the m2 matrices A{jB and write

/AⁿB A¹²B ··· A^lnB\

A®B=l

*}

™

' ' '

*r

I. (2.9)

\AmlB Am2B AwmB ]

An examination of either form of A ® Β shows that Α ® Β is an mn X win square matrix and that (2.7) is a generally valid expression for (A ® B)\

The computation of Kronecker products will be illustrated by evaluating I^zl ® 1² and l^x ® I^z2 for two spin angular momenta with

^i = \ ^{a n o}^ ^2 — 1 · T h e identity operator 72 is represented by a three- dimensional identity matrix, so that

1 1 0

l

°\

1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 - 1 0 0 0 0 0 0 - 1 0 0 0 0 0 0 - 1

2. K R O N E C K E R P R O D U C T S O F L I N E A R T R A N S F O R M A T I O N S 103 Similarly,

1 0 /^{l 0 0}

/ , 2 - * Λ ® / Ζ 2 = (^N J ® 0 0 0

\0 0 - 1

1 0 0 0 0 0N

0 0 0 0 0 0 0 0 - 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 ,0 0 0 0 0 - 1 T h e sum of Izl (Χ) 1² and 7² (X) Iz2 is

0 0 0 ( 0 0 0 ( - \ 0 0 ( 0 \ 0 ( 0 0 - i (

0 0 Ö —Ί

These matrices have all the properties demanded by the dimensionality of the product space and the formula m = m¹ -\- m² .

Further examples of Kronecker products are given in Table 4.1, which lists the 16 possible Kronecker products for two spin-£ nuclei relative to the bases which diagonalize Izl and Iz2 . In this tabulation, 1 denotes the 2 x 2 identity matrix, 0 the 2 x 2 zero matrix, and σχ , σν , and σζ the 2 x 2 Pauli spin matrices.

TABLE 4.1

KRONECKER PRODUCTS

(8) ^2 Ιχ2 Iy2 Iz2

/ / 0\

\_ίσ

\/o

1 ΙΟ

l)

a J

aj

a

I/O I\

Xl

2

\σ

\σ„

1 /1 2 1/ 0 / 4 \ σχ 0 / 4 U^v 0 / 4 \ σζ 0 /

0 \ ΐ Κ 0 \ 1 / α , 0 \

\ίο

21 2 ΙΟ - / / 4 ΙΟ

-ο)

-α)

T h e formula for computing the Kronecker product of two matrices also holds for the vectors eⁱ ®fj of the product basis. Consider, for

104 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S

example, two spin-^ particles. T h e product basis is {| + > ® | + > , I +> ® I ->, I -> ® I +>> I -> ® I ->}> where | ± > = | \ , ± £>, and where the first ket in each product refers to particle 1, the second ket to particle 2. Upon introducing the column vectors for | + > and I — >, one obtains

i+>®i+> = (J)®(J)

I-> ® I+> = (?) ® (i)

C. Diagonalization of Kronecker Products

T h e matrix representative of a Kronecker product Α ® Β depends upon the matrix representatives of A and B. In fact, an examination of the matrix for Α ® Β reveals that it is diagonal if and only if A and Β are diagonal. This result is a direct consequence of equations (2.5) and the theorem on commuting operators (cf. Appendix I).

The matrix which diagonalizes Α ® Β is given by the Kronecker product of the matrices which diagonalize A and B. For if R~^lAR = (Aⁱ 8^ir) and S^BS = (B^j 8^j)t), then

(R ® S)~\A ® B)(R ®S) = R¹ ® S-\A (x)B)R®S = R^XAR ® S^BS, so that

[(R ® S)-\A ® B)(R ® S)]^iS:ra = A^}Bj S^ir 8^js. (2.10) From this equation it follows that the determinant and trace of A ® Β

are given by

det A ® Β = (det A)n(det B)m, (2.11)

tr^ ® Β = Xx A tr B. (2.12) Equations (2.11) and (2.12) are generally valid, since they can be easily

deduced from the weaker assumption that A and Β can be simul- taneously brought into triangular form.

T h e preceding results may be readily generalized. If A, B, C, ...

3. GENERAL THEORY OF S P I N ANGULAR M O M E N T U M 105

(3.5) denote square matrices of dimensions nA y nB y nc y ... which are diagonalized by Ry S^y T^y respectively, then

(A ® Β ® C ® -)tf*...;R-F- = W * R ' >

[(ie-¹ ® S-i ® 7 ^ ® -)(A ®B®C® -)(R ® S ® Τ ®-J]^m...^;rst...

= AiBjCk "· 8ir 8jS 8kt ···, tr ,4 ® 5 ® C ® ··· = tr ^ tr Β tr C ··· .

3. General Theory of Spin Angular Momentum A. The Angular Momentum Operators

T h e mathematical ideas developed in the preceding sections provide the basis for the theoretical treatment of a system of particles with nonvanishing spin angular momenta. T h e general problem can be treated by a straightforward solution of an eigenvalue problem, but considerable expedition can be achieved with the aid of other techniques (3). In this section the general problem will be outlined and derivations of some important results required for subsequent developments will be given.

Let Ν denote the total number of particles, Ij = (Ixj , Iy j, Izj) the vector spin operator for the 7TH particle, and 1 / = 1^ + Iyj + 1% its square. T h e operators I^{x j}, I^{y j}, I^zj, and Iy² satisfy the commutation rules

IV > hj] = 0, , /„,] = iXe^AßvI^vj, (3.1)

V

where j = 1 , 2 , Ν; λ, /Χ, ν = xy y^y ζ; i = V— 1 ; and βλμν is the Levi- Civita tensor density defined in Chapter 2.

T h e spin operators for the ^th particle operate on the vectors of a (21j + l)-dimensional spin space Sj , and the eigenvectors of I? and I^zj constitute a particular basis for Sj . This basis is denoted {| Ij, ntj = —Ij, —13 + 1, i y , and its elements are such that

I,²| / , , m , > = / , ( / , + 1)| /,,*!,>, (3.2)

7^2J

I

ra, I /,·, m,->,

J,± I / , , mi) = [(/, =F m,)(/, ± m, + l)]i/2 | / . , ^m. ± 1>, (³.4)

106 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S

where3

If = I

± il

. (3.6)

The vector space S of the composite spin system is the Kronecker product of the spaces 5^, and its dimension is given by (1.7).

The product basis for S is given by the set of all products of the form 11\ y ^mi) ® I h y ^mù '*' ®\In y ^mN)y ^{D Ut} it will simplify matters if the symbol ® is omitted. Thus a typical element of the product basis will be denoted

I A , ™i> I h y ^m2> "' I h y ^mN> ^ I h y ^m\ y h > ^W2*> J Ν y ^mN>y

with the understanding that the first ket refers to the first particle, the second ket to the second particle, and so forth. If all particles have spin ^ , the notation will often be simplified by writing | + ) for | ^ , and

I — > for I \, — -|>. For example, if Ν = 5, | +H h) will mean I +> Θ I +> ® I —> ® i —> ® I + > · This product ket may also be denoted αα/3/3α.⁴

T h e spin operators associated with any one of the component spaces become operators on the product space by forming the Kronecker product of these operators and identity operators taken from the other component spaces. For example if Xj denotes any spin operator defined on Sj, then Xj becomes an operator on S through the prescription

Xj -> h ® h ®

® Xi ® Λ+i - ®

structed from Xj and Xk' commute if j Φ k. On the other hand, if j = k^y then the operators constructed from Xj and X/ satisfy com-

mutation relations of the same form as those satisfied by Xj and X/.

For example, if Xj = IX J and Xk' = I^{Y K} , then

Ιχΐ -+ Λ ® h "' ®

®

xi ®

® Λ\ ,

Iyk -> Λ ® /² ® Ik-1 ®Iyk ® lk+1 ® ^]N ·

If j Φ ky then the Kronecker products on the right commute, whereas the commutator of these Kronecker products is i times

Λ ® h "' ® lk-i®hk ® h+i "' ® In,

3 T h e " r a i s i n g " a n d " l o w e r i n g " o p e r a t o r s are h e r e d e n o t e d / ± , to facilitate t h e use of subscripts.

4 A l t h o u g h t h e s y m b o l s α, β are n o less concise t h a n | + > , | — >, t h e r e are n o s t a n d a r d symbols for t h e eigenvectors w h e n / > \ . H o w e v e r , t h e D i r a c notation concisely describes the spin states of particles with arbitrary spin q u a n t u m n u m b e r s a n d will b e used t h r o u g h o u t .

3. G E N E R A L T H E O R Y O F S P I N A N G U L A R M O M E N T U M 107 when j = k. Hence all commutation relations satisfied by the operators Xⁱ preserve their form when the Xⁱ are interpreted as operators on the product space S.

T h e notation for the Kronecker products of operators is extremely awkward, and its continued use would considerably inhibit the writing and manipulation of operators referred to the product space S. Hence- forth the symbol ® and the identity factors will be omitted in all operator expressions. Thus the operator on the right of (3.7) will be denoted Xj . It must be emphasized that the various symbols are omitted only for notational convenience, and that the remaining symbols would be meaningless unless the omitted notation is understood to be present without being explicitly written down. For example, the operator product Ιχ$Ι^μΐ€ (j φ k) without the above convention is meaningless, but according to convention, this symbol signifies the operator product of two Kronecker products,

Vi®"' h-i®hi ® h+i "'® J

N)UI

uk ®

®1N)

= h® ·*· h-i ®hi ® h+i "' h - i ®I

k ® h+i "' ®1N = h i

^ ·

With this understanding, all sums and products of operators will be meaningful in their abbreviated form. For example, all the commutation relations satisfied by the spin operators can now be written quite con- cisely as

[ΙΛΆ*]=0, (3.8)

[hi » hk] = ßjk Χ <νΛ,· · (3.9) Ν

Β. The Total Angular Momentum Operators

T h e total spin vector for a system of iV particles is defined as

I (Ιχ ^y I y ^y I ζ) ^ f "^j >

where, in the conventional notation,

h = Σι¹** ( λ = * , ^ * ) , (3.10)

3=1

and Ij = (Ixj , Iyj , Izj). T h e square of the total spin angular momentum is defined as

Ρ = + V +/Λ (3.11)

108 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S

which is equivalent to

P = 21,⁸ + 2 2)21, • I*. (3.12)

3 3 < A"

These definitions are generalizations of the corresponding definitions for a single angular momentum operator. Their significance is that whatever the value of NY the operators I2, Ix , Iy , and Iz satisfy the same commutation relations:

[ P . / J = 0 , (3.13) [Λ , = * · (3.14)

ν

Equation (3.14) follows directly from (3.9), since

[H

XX ^[HI

^{ΧΧΧ^ΑΜΛΛ:}

jι A: j k ν ν

T o prove (3.13), suppose first that λ = z. Since Iz commutes with I; 2 and hjhk for all j" and k, the commutator of 7S and I2 simplifies to

[I y Jz\ ^^^^ [HJHK HIHK y HL\'

3^k I

N o w every term ΊηΣιΙζ1 with / Φ j or k commutes with IxjIxk + hihk >

so that it is necessary to consider only those terms for which / = k and / = But

[HJHK HIHK y HJ ~~\~ HK\ 0,

so that [I2, Iz] = 0, as asserted. Similar arguments can be used to establish the commutation of Ix and Iy with I2.

T h e identity of the commutation properties of I^x , I^y , I^z , and I² with those of the corresponding operators for a single particle permits the formal adaptation of all properties deduced from these relations in Chapter 2 to the general multispin system. In particular, one can introduce the operators

I* = XH* = %Ixi ± i%hi (3.15)

3 3 3

and show that a proper rotation of the cartesian axes through an angle ψ about the unit vector η induces a unitary transformation5

Ν

€

-ί

.\

Y^e-iwij

3

= 1

5 T h e factorization on t h e right side of (3.16) is permissible since [η · Ι, , η · IJ = 0.

3. GENERAL T H E O R Y OF SPIN ANGULAR M O M E N T U M 109

IG(IG + 1)

Since there are glQ identical blocks, the complete submatrix consists of I^G(I^G + 1) times a [gIc(2I^G + l)]-dimensional unit matrix. T h e full matrix for I2 is obtained by forming the submatrices for all classes and assembling them into a diagonal matrix. In other words, the matrix for I² is the direct s u m⁶ of all submatrices of the form described. It must be noted, however, that the spin quantum numbers I^A , I^B , are distinct, so that I2 is not a scalar matrix.

0 0 1 0 0 0

(3.18)

6 See Appendix I.

of the vectors of the spin space S. Moreover, the set of all eigenvectors of the square and ζ component of the total spin angular momentum must have the properties of the most general set of eigenvectors established in Chapter 2. T h u s the eigenvectors of I² and I^z may be partitioned into classes G = A, B, ... such that each class is characterized by the spin quantum number I^G with spin multiplicity g, . T h e total number of eigenvectors is

Xg^Ia(2I^G + 1),

G

and, since this is the maximum number of linearly independent eigen- vectors, it must be equal to the dimension of S:

%glG(2Ic + l)=fl(2Iⁱ + \). (3.17)

G

T h e right-hand member of (3.17) is the dimension of S as determined by the number of elements in the product basis, whereas the left-hand member expresses the dimension of S as determined by an enumeration of the elements in the basis of eigenvectors of I2 and Iz . T h e equality of these numbers expresses the invariance of the dimension of S.

Although the values of IG and gj are not determined by the counting procedures just described, enough information is available to describe the general form of the matrices for I2 and Iz relative to the basis of eigenvectors. Consider first the submatrix of I2 generated by a generic class G. This submatrix has the form indicated in Fig. 4.1. All matrix elements not enclosed by the square blocks vanish, and each block consists of a (21G + l)-dimensional square matrix of the form

110 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S

s⁰ = 2

s^G =3

So ⁼9I(

F I G. 4 . 1 . T h e form of t h e s u b m a t r i c e s of I2 a n d I^z generated by a generic class G of eigenvectors. Each s q u a r e block is a diagonal matrix of d i m e n s i o n 2 I^G + 1 ; all other matrix elements vanish.

T h e submatrix of I^z for class G also has the form shown in Fig. 4.1, except that each subblock has the form

Ig 0

0 Iq 1

Ô Ô

T h e matrix for Iz is obtained by direct summation over all classes.

T h e eigenvectors of I² and l^z will be denoted | I^G , m^G ; s^G}, where s^G = 1, 2, -"ygi^G is the spin multiplicity index,⁷ and G = A, B, ... . These eigenvectors satisfy the orthogonality conditions

<Ικ , \IG>mG; sG} -= 8^KG δ , ^ , , ^ δ , ^ , ^ . (3.20) The spin quantum numbers I^G , their spin multiplicities g, , and the

eigenvectors of I2 and Iz may be determined by an analysis of the eigen- (3.19)

7 T h e spin-multiplicity index will be o m i t t e d w h e n e v e r g , — 1.

3. GENERAL THEORY OF S P I N ANGULAR M O M E N T U M 111 value problem as formulated in the product basis. T h e matrix for Iz

is diagonal, and its diagonal elements are all taken from the sequence

/max > 7m ax 1, /max ~\~ 1> /max > ( 3 . 2 1 )

where

/max

· Ν 3=1

This sequence contains 2 /^{m a x} + 1 terms, and is generated by the distinct values of the total spin variable

m = m1 + m2 + *·· + mN, ( 3 . 2 2 )

(j = 1 , 2 , ...,7V). ( 3 . 2 3 )

Since

2/max + 1 < Π (

> + 0 =

* »

whenever TV is greater than unity,8 all values of m except m = ± /m a x

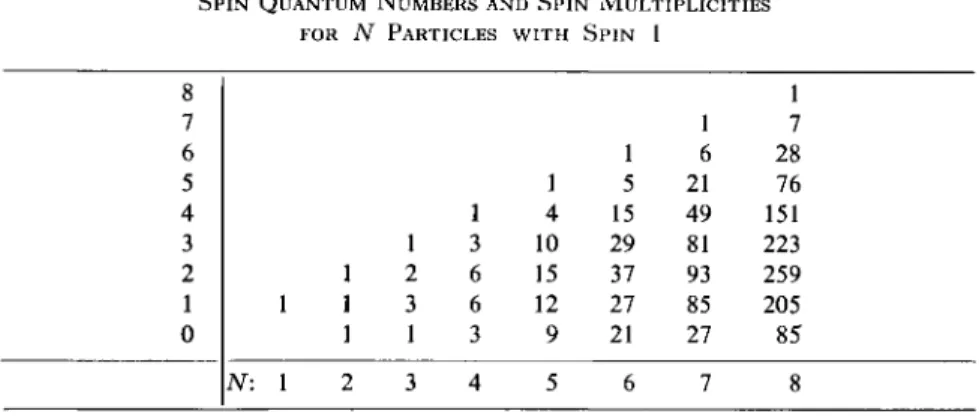
are degenerate. T h e degree of degeneracy of a given value of m, which will be denoted v(m), is equal to the number of ways in which the ntj can be chosen so as to satisfy (3.22), subject to the restrictions imposed by (3.23). Evidently, v(m) has the following properties:

v(m) = v(—m),

K/max)

K-Jmax) =

χ " ( « ) = η

3=1

For small values of N, the values of v(m) may be determined by explicit construction of the product basis. For example, if Ν = 2, and I^x = I² = 1, dim S = ( 2 /^x + l ) ( 2 /² + 1) = 9, and there are 2/ma x + 1 = 2(1 + 1) + 1 = 5 values of m with v{± 2) = 1, v(±\) = 2, K O ) = 3 (Table 4.2). If Ν = 2, and /x = f, /2 = 1, then dim 5 - 1 2 , and there are 2 ( | + 1) + 1 = 6 values of m with v(± f ) = 1, v(± f ) = 2, v( ± i ) = 3 (Table 4.3). T h e values of v(m) for arbitrary values of I± and I2 will be determined in Section 4.E.

8 T h i s s t a t e m e n t can b e p r o v e d b y m a t h e m a t i c a l i n d u c t i o n on N.

112 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S T A B L E 4 . 2

PRODUCT K E T S FOR T W O S P I N S W I T H I1 = I2 = 1

P r o d u c t ket ml m2 m v(m)

1

1 l, l; l, 0 > 1 0 1 2

I 1, 0 ; 1, 1> 0 1 1

1 1, 1; 1, - 1 > 1 - 1 0

1 1 , 0 ; 1, 0 > 0 0 0 3

1

1 1, - 1 ; 1 , 0 > - 1 0 - 1 2

1 1 , 0 ; 1, - 1 > 0 - 1 - 1

1 1, - l ; 1, - i > - 1 - 1 - 2 1

T A B L E 4 . 3

PRODUCT K E T S FOR T W O S P I N S W I T H I1 - 3 ι — ι

— 2 ' i2 — 1

P r o d u c t ket ml m

2

Ι ι

? , | ; i , o >

-2-.

I:

0 1

3 2

3 2

3. G E N E R A L T H E O R Y O F S P I N A N G U L A R M O M E N T U M 113

In the important special case of a spin system consisting entirely of spin-^ particles, a simple combinatorial argument leads to the formula

The sum of v(m) from m = — N/2 to m = +N/2 is 2N, so that (3.25) has all the properties required by (3.24).

T h e preceding results can be used to described the general structure of the matrix for I2 in the product basis. Since I2 commutes with Iz ,

where | ni) and | m'y are abbreviations for two product kets with the indicated eigenvalues of I^z . It follows that the matrix elements of I² vanish unless m' — m. T h u s the matrix for I² is the direct sum of

2 /^{m a x} + 1 submatrices whose dimensions are given by the v(m). T h e

form of the matrix for I² is shown in Fig. 4.2. All matrix elements not enclosed by the diagonal blocks vanish. T h e label in each block spécifies the eigenvalue of I^z\ that is, the submatrices enclosed by these blocks

v(m) (3.25)

<m I l2Iz - /2I2 I my = (m - m')(m \ I² | my = 0,

man

max -2

F I G . 4.2. T h e form of t h e m a t r i x for i2 in t h e p r o d u c t basis. T h e s q u a r e blocks are labeled with the eigenvalues of Iz a n d contain all n o n v a n i s h i n g matrix elements of i2.

114 4. A N G U L A R M O M E N T U M O F M U L T I S P I N S Y S T E M S

are generated by elements in the product basis with the indicated value of M. Since v ( ± /^{m a x}) = 1, it follows that the two products kets I Ix , ±I± ; 12 , ± /² î ··· ï IN Y ± ^ J V ) ^{a re} eigenvectors of I² with the eigenvalue I^mQlX(I^max + 1). This may be directly verified by introducing the operator identity

Ii · Ifc = ',Λ* + Wfh- + W ) (3.26) into the expression for I², obtaining

I2 =

2 ^V

^£27

^,/

22 ^{( W +}

j i < i < A*

and operating with I² on | I^x , ; I^N , ± /^N> . These kets are but two of the 2 /^{m a x} + 1 spin states associated with a spin quantum number I = I^{m ax} . T h e remaining 2 J^{m ax} — 1 states with / = /^{m a x} , and all other spin quantum numbers, are obtained by diagonalizing9 the sub- matrices of I2 whose dimensions exceed unity.

It is clear that no spin quantum number can exceed /^{m a x} , and, since v ( /^{m a x}) = 1, £ /^{m ax} = 1 · T h e spin quantum numbers will be of the form (cf. Section 3.E)

I 1

Anax j ^Anax

^/max

^/

^{i n}

where the spin quantum number 7m i n is implicitly defined by the condi- tion

Vax ^Ν

X g,(2I+\) = Π (2Λ + 1). (3.29)

F— W „_1

C. Systems with Spin \

When the spin quantum numbers have been determined, sets of linear equations can be formed whose solutions can be used to express the eigenvectors of I² and I^z as linear combinations of elements in the product basis (3). However, the results required most frequently in the analysis of high-resolution spectra are the values of the spin quantum numbers and their multiplicities for systems composed of identical

9 T h e matrices for I2 a n d Iz , relative to t h e p r o d u c t basis, have b e e n labeled b y t h e values of t h e total spin variable m. U p o n r e d u c t i o n to diagonal form, these matrices will not, in general, have t h e diagonal form described previously, b u t t h e desired form can b e achieved by s o m e trivial i n t e r c h a n g e s of rows a n d c o l u m n s in t h e matrices for I2, Iz , a n d t h e diagonalizing u n i t a r y m a t r i x .

3. GENERAL THEORY OF S P I N ANGULAR M O M E N T U M 115

particles with all Ij — \ . These results can be deduced without solving the eigenvalue problem, but before carrying out the analysis, the explicit solution of the eigenvalue problem will be illustrated for some relevant special cases.

1. Ν = 2. T h e product basis is {| + + > , | + - > , | - + > , | >}, whose elements are represented by the column vectors determined in Section 2.B. Operating on the product kets with Iz = I^zl + I^z2, one obtains

/, I + + > = ι · Ι + +>, h I + - > = ο · | + - > ,

i^z\-+> = 0 - | - + > , I9\ > = - 1- 1 — > . These equations show that the matrix for Iz is

(

1

0 0 0 0 Γ 0 0 0 - 1 /

a result which could have been written down immediately by adding the Kronecker products for I^zl (x) 1² and 1^λ ®I^z2 given in Table 4.1.

T h e product kets | + + > and | > are eigenvectors of I2 = Ιχ2 + I2 2 + 2IZ1IZ2

+ v /

- + /

/

,

both eigenvectors corresponding to a total spin of 7m a x = Ix + I2 —

^ - f \ = 1. T h e only other possible value of / allowed by (3.28) is

1

= Anax

Λ( 2 · 1 + 1 ) +Λ( 2 · 0 + 1) = 2·.

T h e matrix for I2 may be obtained from the following calculations:

ι

1 + - > = ( ! - + - ! - έ){ΐ + - > + 1 - + > } = ι + - > + 1 —+>, ι

1 - + > = ( I + t - J X I - + > + I + - > } = I + - > + I - + > .

<+— 11

1 + - > = <—+11

1 + - > = < + - 1 1

1 - + > = 1;

hence

(

ο ι ι ο I

0 0 0 2 /

T h e matrix for I² may also be obtained from Table 4.1.