stable set for coalition function form games The equivalence of the minimal dominant set and the myopic Games and Economic Behavior

Contents lists available atScienceDirect

Games and Economic Behavior

www.elsevier.com/locate/geb

The equivalence of the minimal dominant set and the myopic stable set for coalition function form games ^✩

P. Jean-Jacques Herings

^a

^,∗ , László Á. Kóczy

^b

^,

^c

aDepartmentofEconomics,MaastrichtUniversity,P.O.Box616,6200MD,Maastricht,theNetherlands bCentreforEconomicandRegionalStudies,TóthKámánu.4.,1097Budapest,Hungary

cDepartmentofFinance,FacultyofEconomicsandSocialSciences,BudapestUniversityofTechnologyandEconomics, Magyar tudósok körútja 2,1117Budapest,Hungary

a rt i c l e i nf o a b s t ra c t

Articlehistory:

Received29May2020

Availableonline20February2021

JELclassification:

C71

Keywords:

Coalitionstructurecore Sequentialdominance

Incooperativegames,thecoalitionstructurecoreis,despiteitspotentialemptiness,oneof themostpopularsolutions.Whileitisafundamentallystaticconcept,theconsideration of a sequential extension of the underlying dominance correspondence gave rise to a selection of non-empty generalizations. Among these, the payoff-equivalence minimal dominant set and the myopic stable set are defined by asimilar set ofconditions. We identifysomeproblemswith thepayoff-equivalenceminimal dominantset and propose an appropriatereformulation called the minimaldominant set.We show that replacing asymptoticexternalstabilitybysequentialweakdominanceleaves themyopicstableset unaffected.Themyopicstablesetisthereforeequivalenttotheminimaldominantset.

©^{2021TheAuthor(s).PublishedbyElsevierInc.Thisisanopenaccessarticleunderthe} CCBYlicense(http://creativecommons.org/licenses/by/4.0/).

1. Introduction

Thecoreisoneofthemostpopularsolutionconcepts incooperativegametheory.Itintroduces acoalitionalnotionof stability not unlike theNash equilibrium:once sucha proposalismade, it isnot abandoned.The similarities gofurther:

neither oftheseconcepts tellushow such agreements arereached. Suppose thegame starts withan arbitraryproposal:

howtomovefromthisproposaltoanacceptable,equilibriumallocation?

To ourknowledge Stearns (1968) wasthe first to lookat thisproblem by considering a recontractingprocess where myopic deviationsbycoalitions areconsidered asimprovements.Green(1974), Neuefeind(1974),andWu(1977) present resultsthatsuch improvementsalmost surelyorapproximatelyreachthecore.TheresultsofArnoldandSchwalbe(2002) extendeventoNTU-games.Morerecently,RothandVandeVate(1990),Diamantoudietal.(2004),KlausandKlijn(2007) andChen etal.(2016) show formatchingmarkets andSenguptaandSengupta (1994,1996), KóczyandLauwers(2004), andKóczy(2006) showforcoalitionalgamesthatthecorecanactuallybereached.Thelatterresultsprovetheexistenceof an upperboundonthenumberofstepsneeded.Thisboundhassincebeendrasticallylowered(Yang,2010,2011; Béalet al.,2012,2013a,b).

✩ KóczythanksthesupportoftheNationalResearchDevelopmentandInnovationOffice (NKFIH)undergrantnumberK-128573. Thisresearchwas supportedbytheHigherEducationInstitutionalExcellenceProgram2020oftheMinistryofInnovationandTechnologyintheframeworkofthe‘Financial andPublicServices’researchproject(TKP2020-IKA-02)atCorvinusUniversityofBudapest.

*

Correspondingauthor.

E-mailaddresses:P.Herings@maastrichtuniversity.nl(P.J.J. Herings),koczy@krtk.mta.hu(L.Á. Kóczy).

https://doi.org/10.1016/j.geb.2021.02.003

0899-8256/©^{2021TheAuthor(s).PublishedbyElsevierInc.ThisisanopenaccessarticleundertheCCBYlicense} (http://creativecommons.org/licenses/by/4.0/).

It is naturalto ask wheredo thesecoalitionalimprovements lead in casethecore is(possibly) empty.Sengupta and Sengupta (1994) define the setofviableproposals, Kóczyand Lauwers(2007) the payoff-equivalenceminimaldominantset¹ andmostrecentlyDemuyncketal.(2019) themyopicstableset.Alltheseconceptsrelyonnotionsofsequentialdominance andbelongtothefamilyofstochasticsolutions(Packel,1981)withappropriaterestrictionsonthepermittedtransitions.

We identifya probleminthedefinitionof thepayoff-equivalence minimaldominantset; underthecurrentdefinition Theorem 4 ofKóczy andLauwers(2007) does nothold. The problemiscaused bythe incorporationof payoff-equivalent outcomesinthedominancecorrespondence.Wearguethatpayoffequivalenceshouldbedropped,whichleadstothenotion ofthe minimaldominantset.Wego onto show thatthe minimal dominantsetandthemyopic stablesetare equivalent, whereforthelatterconceptitdoesnotmatterwhetherstrictorweakdominanceisusedinthedefinition.Itthenfollows fromYang(2020) thatbothconceptsareincludedinthesetofviableproposals.

Accordingly, the structure of thepaper is asfollows. First,we introduce the basic terminologyand notation together withboththepayoff-equivalentminimaldominantsetandtheminimaldominantset.Thenweintroducethemyopicstable set anditsvariant basedonweak dominance calledtheweak dominancemyopic stableset.We presentourmain result showingtheequivalenceoftheminimal dominantset,themyopic stableset,andtheweakdominancemyopic stableset.

Finally, forthe class of proper simple games, we presenta general resultof payoff equivalence of the payoff-equivalent minimaldominantset,theminimaldominantset,andthemyopicstableset.

2. Thepayoff-equivalenceminimaldominantset

A characteristicfunction formgame isdefinedby a pair

(

N

,

v

)

,where N is a setof playerswithcardinalityn anda characteristicfunctionv

:

^2N

→

R^{thatassignstoeachcoalitionC}

⊆

^{N anumberv}

(

C

) ∈

R^{,calledtheworthofC,withthe} usualconventionthat v

( ∅ ) =

^{0.Thecollectionofnon-emptycoalitionsisdenotedby}N^{.Acoalitionstructureisapartition} P

= {

^C1

, . . . ,

C^m

}

^{ofN.Itdescribeshowthegrandcoalitionisdividedinto}non-overlappingsubcoalitions.Thecollectionof allcoalitionstructures,thatis,thecollectionofpartitionsofN,isdenotedby

.ForacoalitionC

∈

N,let

C

denotethe partitionintosingletoncoalitions.Formally,wehavethat

^C

= {{

ⁱ

} |

ⁱ

∈

^C

}

^.

ForacoalitionstructureP

∈

andacoalitionD

∈

N^{,thepartners’set P}

(

D

,

P

)

ofD inP^{istheunionofthosecoalitions} inPthathaveanon-emptyintersectionwithD,theresidualplayers R

(

D

,

P)aretheplayersinthepartners’setoutsideD andtheoutsiders O

(

D

,

P)^{arealltheplayersoutsidethepartners’set,somoreformallywehave}

P

(

D

,

P

) =

C∈P,C∩^D=∅

C

,

(2.1a)

R

(

D

,

P

) =

^P

(

D

,

P

) \

^D

,

(2.1b)

O

(

D

,

P

) =

^N

\

^P

(

D

,

P

).

(2.1c)

Thecollectionofcoalitionstowhichtheoutsidersbelongisgivenby O

(

D

,

P

) = {

^O

∈

P

|

^O

∩

^D

= ∅} .

Forcoalitionfunctionformgames,we definethesetofoutcomes X asthesetofcoalitionstructures

together withall individually rational payoff vectorsthat can be obtainedby allocating the worthsamong themembers of therespective coalitions:

X

=

(

P

,

u

) ∈ × R

^N

| ∀

ⁱ

∈

^N

,

u_i

≥

^v

({

ⁱ

})

^and,

∀

^C

∈

P

,

i∈C

u_i

=

^v

(

C

)

.

Givenan outcome x

∈

^{X,we denoteby}P(^x

)

the projectionto itsfirst component,that is,thecoalitionstructure, andby u

(

x

)

the projection to its second component, that is,thepayoff vector. We can thus write x

= (

P

(

x

),

u

(

x

))

. The set X is non-empty sinceitalwayscontains theoutcome xwhereN ispartitionedintosingletons,so P

(

x

) =

^N

^{,andeachplayer} i

∈

^{N receivesthepayoff v}

( {

ⁱ

} )

.

KóczyandLauwers(2007) definethenotionofoutsider-independent dominance,towhichwewillreferasweakdomi- nanceinthispaper.

Definition2.1.Anoutcome y

∈

^{X weaklydominatesanoutcomex}

∈

^{X bydeviating}coalition D if

•

P(^y

) = {

^D

} ∪

^R

(

D

,

P(^x

)) ∪

O(^D

,

P(^x

))

, and

1 KóczyandLauwers(2007) usetheterminologyminimaldominantset,butfollowingthelaterliteraturewereservethistermforadifferentconcept.

•

^foreveryi

∈

^D,ui

(

y

) ≥

^ui

(

x

)

andthereexistsi

∈

^Dsuchthatui

(

y

) >

ui

(

x

)

,

•

^foreveryi

∈

^O

(

D

,

P(^x

))

,u_i

(

y

) =

^ui

(

x

)

.

After a coalition D deviates, theresidual playersfall apartintosingletons,whereas theoutsiders stayintheir original coalitions. Utilities ofoutsiders arenot affected, whereas theutilities ofthe deviating playersall weaklyimprove andat least one deviating player strictly improves. Since y

∈

^{X, it follows fromDefinition 2.1that}

i∈^Dui

(

y

) =

^v

(

D

)

and, for everyi

∈

^R

(

D

,

P(x

))

,ui

(

y

) =

^v

( {

ⁱ

} )

.Thetreatmentofresidualplayerscorrespondstothe

γ

-modelofHartandKurz(1983).

ThepropertythatoutsidersarenotaffectedbyacoalitionaldeviationisalsoreferredtoascoalitionalsovereigntyinKonishi andRay(2003),RayandVohra(2014,2015),andHeringsetal.(2017).

Oneofthemostprominentset-valuedsolutionconceptsforcoalitionfunctionformgamesisthecoalitionstructurecore asdefinedinAumannandDrèze(1974).

Definition2.2.Thecoalitionstructurecore(CSC)of

(

N

,

v

)

isthesetofoutcomesx

∈

^{X suchthat,foreverycoalitionC}

∈

N,

i∈C

ui

(

x

) ≥

v

(

C

).

Inwords,thecoalitionstructurecoregivestothemembersofeachcoalitionatleastthepayofftheycanobtainbyforming thatcoalition.Itiseasytoprovideexampleswherethecoalitionstructurecoreisempty.

Letsome outcome x

∈

^{X be given. The set ofall outcomes that weaklydominate x together withoutcome x itself is} denotedby g

(

x

)

,so

g

(

x

) = {

^x

} ∪ {

^y

∈

^X

|

^{there isD}

∈

N such thatyweakly dominatesxbyD

} .

We definethetwo-foldcompositionof g by g²

(

x

) = {

^z

∈

^X

| ∃

^y

∈

^g

(

x

)

such thatz

∈

^g

(

y

) }

^{.Byinduction,we definethek-} folditeration g^k

(

x

)

asthesubsetof X thatcontainsalloutcomesobtainedbyacompositionofdominancecorrespondences of length k

∈

N^{,that is, gk}

(

x

) = {

^z

∈

^X

| ∃

^y

∈

^gk−1

(

x

)

such thatz

∈

^g

(

y

) }

^{. Observe that forevery k}

, ∈

N ^ifk

≤

,then g^k

(

x

) ⊆

g

(

x

)

.Wedefinethesetofalloutcomesthatcanbereachedfromxbyafinitenumberofdominationsby g^N

(

x

)

, so

g^N

(

x

) =

k∈Ng^k

(

x

).

Theoutcomesx

,

y

∈

^{X arepayoffequivalentifu}

(

x

) =

^u

(

y

)

.Thenotionofpayoffequivalencepartitionsthesetofoutcomes into equivalence classes. We denote the equivalence class containing x by

[

^x

]

^{. Kóczy and Lauwers (2007) say that the} outcome y

∈

^{X isaccessiblefromtheoutcome x}

∈

^{X ify}

∈

^gN

(

x

)

or y ispayoffequivalent tox.Thesetofoutcomesthat areaccessiblefromxinthesenseofKóczyandLauwers(2007) canthereforebewrittenas

g

^N

(

x

) =

^gN

(

x

) ∪ [

^x

].

Thecorrespondence_gNmayfailtobetransitive.Asweareconsideringoutcomesaccessiblefromaccessibleoutcomesitis naturaltoconsideritstransitiveversion:

g

(

x

) =

g

(

x

) ∪ [

x

].

We define its two-foldcomposition by g²

(

x

) = {

^z

∈

^X

| ∃

^y

∈

^g

(

x

)

such thatz

∈

^g

(

y

)}

^{. Byinduction, we define the k-fold} iteration g^k

(

x

)

asthe subset of X that contains all outcomes obtainedby a composition ofdominance correspondences of length k

∈

N^{,that is, gk}

(

x

) = {

^z

∈

^X

| ∃

^y

∈

^gk−1

(

x

)

such thatz

∈

^g

(

y

) }

^{. Observe that forevery k}

, ∈

N ^ifk

≤

,then g^k

(

x

) ⊆

^g

(

x

)

.Wedefinethesetofalloutcomesthat canbereachedfromxbyafinitenumberofdominationsandpayoff equivalencesby g^N

(

x

)

,so

g^N

(

x

) =

k∈Ng^k

(

x

).

Itiseasilyseenthat

g^N

(

x

) ⊇

_g

N

(

x

) =

^gN

(

x

) ∪ [

^x

].

Inthispaper,wesaythattheoutcome y

∈

^{X isaccessiblefromtheoutcomex}

∈

^{X if y}

∈

^gN

(

x

)

.

Definition2.3.Let

(

N

,

v

)

be a coalition function form game. The set

⊆

^{X isa} payoff-equivalenceminimaldominantset (PEMDS)ifitsatisfiesthefollowingthreeconditions:

1. Closure:Foreveryx

∈

,g^N

(

x

) ⊆

.

2. Accessibility:Foreveryx

∈ / ,

g^N

(

x

) ∩ = ∅

^.

3. Minimality:Thereisnoset

thatsatisfiesConditions1 and2.

Wearguenextthatmultiplepayoff-equivalenceminimaldominantsetscannotco-exist.Theargumentreliesheavilyon thetransitivityofg^N.

Theorem2.4.Acoalitionfunctionformgame

(

N

,

v

)

canhaveatmostonePEMDS.

Proof. Let

1 and

2 both be a PEMDS of

(

N

,

v

)

. We argue that

1

∩

2 satisfies Closure andAccessibility,which by Minimalityimpliesthat

1

=

2.NoticethatAccessibilityof

1

∩

2impliesthat

1

∩

2

=

∅^.

ToshowClosurefor

1

∩

2,letx

∈

1

∩

2 andy

∈

^gN

(

x

)

.Thengiventhatx

∈

1and

¹satisfiesClosure,itmustbe that y

∈

1.Alsogiventhatx

∈

2 and

2 satisfiesClosure,itmustbethat y

∈

2.Thisimpliesthat y

∈

1

∩

2 aswas tobeshown.

ForAccessibility,takeanyx

∈ /

1

∩

2.Therearethreecasestoconsider.

Case1.x

∈

1

\

2.Then, byAccessibility of

2,there is y

∈

2 such that y

∈

^gN

(

x

)

.ByClosureof

1,wehavethat y

∈

1.Thismeansthat y

∈

1

∩

2,whichiswhatweneededtoshow.

Case2.x

∈

2

\

1.TheproofissymmetrictoCase 1with

1 and

2interchanged.

Case3.x

∈

^X

\ (

1

∪

2

)

.Weknow,byAccessibilityof

1,thatthereis y

∈

1 suchthat y

∈

^gN

(

x

)

.If y

∈

2,weare done. Ifnot,thenwe knowfromCase 1that thereis z

∈

1

∩

2 suchthat z

∈

^gN

(

y

)

.It followsfromtransitivity of g^N that z

∈

^gN

(

x

)

.

Kóczy andLauwers(2007) also assertexistence ofa PEMDSfora coalitionfunction formgame

(

N

,

v

)

.Unfortunately, Kóczy and Lauwers (2007) do not use Accessibility consistently, formost of the paper the correspondence g^N is used interchangeablywith _gN.MostnotablyTheorem 4ofKóczyandLauwers(2007) isfalse.Theproblematicassertionisthat thereexistsanaturalnumber

τ ∈

N^{suchthatforalloutcomesx}

,

y

∈

^{X wehavethat y}

∈

_gN

(

x

)

ifandonlyify

∈

^gτ

(

x

)

.

Thefollowingisacounterexample.

Example2.5.Consider a game with N

= {

¹

,

2

}

^{and v}

(

C

) = |

^C

|

^{for all C}

⊆

^{N and the outcome x where} P

(

x

) = {

^N

}

^and u

(

x

) = (

1

,

1

)

.ThisisanelementofthecoalitionstructurecoreCSC andthereforeg

(

x

) =

^gN

(

x

) = {

^x

}

^{.Ontheotherhandthe} outcome ywhereP

(

y

) =

^N

^andu

(

y

) =

^u

(

x

)

ispayoffequivalent toxandistherefore,bydefinition,accessible.Contrary totheassertionoftheaforementionedTheorem,wehavethat y

∈

_gN

(

x

) ⊆

^gN

(

x

)

,whereas y

∈ /

^gN

(

x

)

.

3. Theminimaldominantset

It is clear that payoff equivalence causes problems, while it turns out that it is completely superfluous and can be eliminated.Inthissectionwedroppay-off equivalencefromthedominancecorrespondence.Otherpapersintheliterature studyingthepayoff-equivalenceminimaldominantsethavedonesoaswell,seeforinstanceYang(2011,2020).Thismakes also sense froma conceptual point of view.For a new coalition to form, atleast one of the coalition members should improve,whichisnotthecaseunderpayoffequivalence.

Definition3.1.Let

(

N

,

v

)

beacoalitionfunctionformgame.Theset

⊆

^{X isaminimaldominantset(MDS)ifitsatisfiesthe} followingthreeconditions:

1. Closure:Foreveryx

∈

,g^N

(

x

) ⊆

.

2. Sequentialweakdominance:Foreveryx

∈ /

,g^N

(

x

) ∩ = ∅

^. 3. Minimality:Thereisnoset

thatsatisfiesConditions1 and2.

Definition3.1isobtainedfromDefinition2.3byreplacingthecorrespondence g^Nby g^N.The onlydifferencebetween thesecorrespondencesistheabsenceofpayoffequivalenceinthelatter,soforevery x

∈

^{X itholdsthat gN}

(

x

) ⊆

^gN

(

x

)

.

TheproofofTheorem 4ofKóczyandLauwers(2007) reliesonaconstructionwherethesetofoutcomesispartitioned intosimilarity classes.Similarityclassesareclosed andconvexsets ofoutcomesdeterminedby thecoalitionaldeviations they are subjectto.Notably, twodistinct payoff-equivalentoutcomesbelong to differentsimilarityclasses andtheir pay- off equivalenceis not takeninto accountat all.As a result, ifwe replace Accessibility withSequentialweak dominance, Theorem 4ofKóczyandLauwers(2007) holds.

Theorem3.2.Let

(

N

,

v

)

beagame.Thenthereexistsanaturalnumber

τ ∈

N^{suchthatforalloutcomesx}

,

y

∈

^{X wehavethat} y

∈

^gN

(

x

)

ifandonlyify

∈

^gτ

(

x

)

.

Whilethisresultpresentsnoexplicitbounds,Yang(2011) showsthatelementsoftheMDScanbereachedinanumber ofstepsthatisquadraticinn.

Next,wecanproceedasinKóczyandLauwers(2007) toshowthefollowingresult.

Theorem3.3.Acoalitionfunctionformgame

(

N

,

v

)

hasauniqueMDS.Ifthecoalitionstructurecoreofthegameisnon-empty,then itisequaltotheMDS.

It followsfrom a counterexamplein Bhattacharya andZiad(2006) that Theorem 3.3cannot be extended to thenon- transferableutilitycase;Kóczy(2018,p. 99) conjecturesthesameforpartitionfunctionformgames.

Whatistheeffectoftheremovalofpayoffequivalenceonthesolutionconcept?Notethatforagenericcoalitionfunction formgame

(

N

,

v

)

,ifP,Q

∈

aredifferentpartitionsofN,soP

=

Q^,then

C∈Pv

(

C

) =

C∈Qv

(

C

)

.

Theorem 3.4.Let

(

N

,

v

)

be a coalitionfunction formgame suchthat, forevery P,Q

∈

suchthatP

=

Q^,

C∈Pv

(

C

) =

C∈Qv

(

C

)

.Then

isanMDSof

(

N

,

v

)

ifandonlyifitisaPEMDSof

(

N

,

v

)

.

Proof. TheassumptionofTheorem3.4impliesthatpayoffequivalencescannotoccur.Therefore,itholdsthat g^N

=

^gN. Theorem3.4establishesthatforgenericcoalitionfunctionformgames,thePEMDScoincideswiththeMDS.

Apartfromthegenericcasewheremultiplepartitionswiththesametotalpayoffdonotexist,thereisanotherinteresting classofcoalitionfunctionformgameswherethepredictionsofPEMDSandMDScoincide,that is,coalitionfunction form gameswithanon-emptycoalitionstructurecore.

Theorem3.5.Let

(

N

,

v

)

beacoalitionfunctionformgamewithanon-emptycoalitionstructurecore.ThenthePEMDSof

(

N

,

v

)

is equaltothecoalitionstructurecore.

Proof. We arguefirst that anyelement ofthe coalitionstructure corebelongs toa PEMDS. Assume that

isa PEMDS.

Let x

∈

^{CSC. It holds that gN}

(

x

) = {

^x

}

^{. Forevery y}

∈ [

^x

]

^{, it holds that y belongs to CSC, so gN}

(

y

) = {

^y

}

^{and therefore} g^N

(

x

) = [

^x

]

^.

Suppose x

∈ /

.Then, wehave g^N

(

x

) ∩ = [

^x

] ∩ = ∅

^.Closureof

nowimplies

[

^x

] ⊆

,contradicting x

∈ /

.Conse- quently,itholdsthatx

∈

.

We arguethat CSC satisfies Closure andAccessibility,whichby Minimality impliesthat

=

^{CSC.We alreadyshowed} thatforeveryx

∈

^{CSC wehavegN}

(

x

) = [

^x

]

^{.ThisshowsClosure.}

By Theorem 3.3, it holds that the MDS of

(

N

,

v

)

is equal to CSC, so CSC satisfies Sequential weak dominance and thereforeAccessibility.

It followsfromTheorems 3.3and3.5thattheMDS andthe PEMDScoincide forcoalitionfunctionformgameswitha non-emptycoalitionstructurecore.

WenowpresentanexamplewheretheMDSisapropersubsetofthePEMDS.

Example3.6.Let

(

N

,

v

)

be the three-playersimple majoritygame,so N

= {

¹

,

2

,

3

}

^{and v}

( {

¹

,

2

} ) =

^v

( {

¹

,

3

} ) =

^v

( {

²

,

3

} ) =

v

(

N

) =

^{1,whereastheworthofanyothercoalitionisequaltozero.ItholdsthatCSC}

= ∅

^.LetM

= {{

¹

,

2

} , {

¹

,

3

} , {

²

,

3

}}

^be thesetofminimalwinningcoalitions.Considertheset F

⊆

^{X definedby}

F

= {

^x

∈

^X

|

P

(

x

) ∩

M

= ∅} ,

so in payoffterms the set F isgiven by thefacets ofthe unit simplex. It iseasily verified that F satisfiesClosure with respectto g^N andAccessibility.Moreover, forevery x

∈

^{F,itholdsthat gN}

(

x

) =

^{F,sothereisnopropersubset ofF that} satisfiesClosurewithrespectto g^N andAccessibility.ItfollowsthattheMDSof

(

N

,

v

)

isequalto F.Thepredictionofthe MDSisthataminimalwinningcoalitionformsandoneplayerbecomesasingleton.Itisexcludedthatthegrandcoalition forms.

ThesetF isnotaPEMDS,sinceoutcomeswhicharepayoffequivalenttooutcomesinF maynotbelongtoF themselves.

Forinstance,foreveryx

∈

^{F itholdsthat y}

∈

^{X definedby}P

(

y

) = {

^N

}

^andu

(

y

) =

^u

(

x

)

ispayoffequivalenttox,butisnot partof F.WedefinethesetF

⊆

^{X by}

F

=

F

∪ {

x

∈

X

|

P

(

x

) = {

N

}

and there existsi

∈

Nsuch thatui

(

x

) =

0

}

= {

^x

∈

^X

|

P

(

x

) ∩ (

M

∪ {

^N

}) = ∅

and there existsi

∈

^{Nsuch thatu}i

(

x

) =

⁰

}.

ItiseasilyverifiedthatthePEMDSof

(

N

,

v

)

isgivenby F.

Example3.6presentsanexamplewherethePEMDSisdifferentfromtheMDS,butthesamewhenprojectedtothespace ofpayoffs.Thisturnsouttobeageneralfeatureofso-calledpropersimplegamesaswewillformallystateinTheorem6.1.

Itisnaturaltoaskifthepropertyholdsingeneral:shouldweignorepartitionsandfocusonthepayoffvectorsonly,dowe haveequivalence?Thenextexampleanswersthisquestioninthenegative.

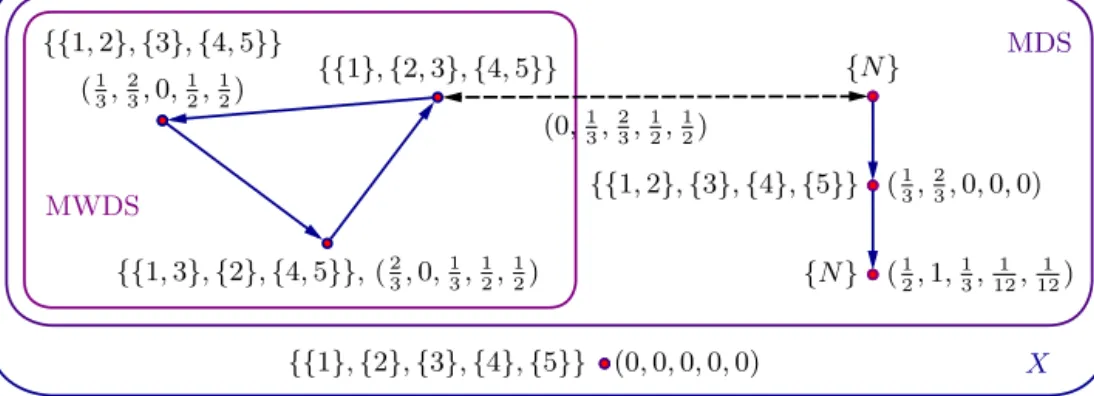
Fig. 1.An illustration of Example3.7. Arrows indicate weak dominances, dashed lines payoff equivalence. Not all weak dominances are displayed.

Example3.7.Considerthefollowing5-playerexample.Coalitions

{

1

,

2

} , {

1

,

3

}

,and

{

2

,

3

}

haveaworthof1;sodoescoalition

{

⁴

,

5

}

^{.Thegrandcoalition}

{

¹

,

2

,

3

,

4

,

5

}

^{hasaworthof2.}

TheMDSequalstheunionofthefacetsofthesimplexonplayers

{

¹

,

2

,

3

}

^{,withoneofthetwo-playersubsetsforming} asa coalition,plus an arbitrarypayoffdivision of theworth of1 ofcoalition

{

⁴

,

5

}

^{.The grandcoalitiondoesnot havea} profitabledeviationfromthis,soisnotpartoftheMDS.Ontheotherhand,itispartofaPEMDS

bypayoffequivalence.

Now atleast one of the coalitions

{

¹

,

2

} , {

¹

,

3

}

^{, or}

{

²

,

3

}

^{can deviate, andplayers 4 and5 become} singletons. Now the grandcoalitioncandeviatewithapayoffvectordifferentfromanypayoffvectorintheMDS.OnecanshowthatthePEMDS containsmuchmoreoftheoutcomesalthoughnotall–withonetrivialexampleindicatedinFig.1.

4. Themyopicstableset

Demuynck et al.(2019) introduce the solutionconcept ofthe myopicstableset forgeneral social environments. They then use theconcept to study specific social environments comingfromapplications like coalitionfunction formgames, matchingmodels,networks,andnon-cooperativegames.Wenowexplainhowthesolutionconceptisdefinedwhenapplied tocoalitionfunctionformgames.

Definition4.1.Anoutcome y

∈

X dominatesanoutcome x

∈

^{X bydeviating}coalition D if

•

P

(

y

) = {

^D

} ∪

^R

(

D

,

P

(

x

)) ∪

O

(

D

,

P

(

x

))

, and

•

^foreveryi

∈

^D,ui

(

y

) >

ui

(

x

)

,

•

^foreveryi

∈

^O

(

D

,

P(x

))

,ui

(

y

) =

^ui

(

x

)

.

The only difference betweenDefinitions 2.1 and4.1 is that the condition that at leastone memberof the deviating coalitionstrictlyimproveshasbeenreplacedbytherequirementthatallmembersofthedeviatingcoalitionstrictlyimprove.

Letsome outcomex

∈

^{X begiven. Thesubset ofX consistingofalloutcomesthatdominatextogetherwithoutcome x} itselfisdenotedby f

(

x

)

,so

f

(

x

) = {

^x

} ∪ {

^y

∈

^X

|

^{there isD}

∈

Nsuch thatydominatesxbyD

} .

As before, we define the two-fold composition of f by f²

(

x

) = {

^z

∈

^X

|∃

^y

∈

^f

(

x

)

such thatz

∈

^f

(

y

) }

^{. By induction, we} define the k-fold iteration f^k

(

x

)

asthe subset of X that contains all outcomesobtainedby a composition ofdominance correspondencesoflengthk

∈

N^{,thatis, fk}

(

x

) = {

^z

∈

^X

|∃

^y

∈

^fk−1

(

x

)

such thatz

∈

^f

(

y

) }

^{.Observethatforeveryk}

, ∈

N^if k

≤

,then f^k

(

x

) ⊆

^f

(

x

)

.Wedefinethesetofalloutcomesthatcanbereachedfromxbyafinitenumberofdominations by f^N

(

x

)

,so f^N

(

x

) =

k∈Nf^k

(

x

)

.

Anoutcome y issaidtoasymptoticallydominatetheoutcomexifstartingfromx,itispossibletogetarbitrarilycloseto y inafinitenumberofdominations.Wedefinethemetricdon X bysettingforeveryx

,

y

∈

^X,

d

(

x

,

y

) = 1

{P(x)=P(y)}

+

^u

(

x

) −

^u

(

y

)

∞

,

where1^{istheindicatorfunctionand}

·

∞istheinfinitynorm.

Notice that payoff-equivalent outcomeswith differentunderlying partitions are not neardue tothe first term ofthe metric.

Definition4.2.Anoutcome y

∈

X asymptoticallydominatesanoutcome x

∈

^{X ifforevery}

ε >

0 thereexistsanumberk

∈

N andanoutcomez

∈

^fk

(

x

)

suchthatd

(

y

,

z

) < ε

.

Wedenoteby f^∞

(

x

)

thesetofalloutcomesin X thatasymptoticallydominatex.Formally,wehave f^∞

(

x

) = {

^y

∈

^X

|∀ ε >

0

, ∃

^k

∈ N, ∃

^z

∈

^fk

(

x

) :

^d

(

y

,

z

) < ε }.

Itiseasytoseethattheset f^∞

(

x

)

coincideswiththeclosureoftheset f^N

(

x

)

. Wearenowreadytodefinethemyopicstableset,abbreviatedasMSS.

Definition4.3.Let

(

N

,

v

)

bea coalitionfunctionformgame.Theset M

⊆

^{X isa myopicstableset(MSS) ifitisclosedand} satisfiesthefollowingthreeconditions:

1. Deterrenceofexternaldeviations:Foreveryx

∈

^{M, f}

(

x

) ⊆

^M.

2. Asymptoticexternalstability:Foreveryx

∈ /

^{M, f∞}

(

x

) ∩

^M

= ∅

^.

3. Minimality:ThereisnoclosedsetM^{MthatsatisfiesConditions1 and2.}

Let M be an MSS. Deterrence of external deviations requires that no coalition can profitably deviate to an outcome outside M.Asymptoticexternalstability requiresthatanyoutcome outsideM isasymptoticallydominatedbyanoutcome inM.Hence,fromanyoutcomeoutsideofMitispossibletogetarbitraryclosetoanoutcomeinM byafinitenumberof dominations.Observethat anempty setwouldnecessarilyviolate externalstability,soanyMSSisnon-empty.Minimality imposes that there is no smallerclosed set of outcomesthat satisfies Deterrence ofexternal deviationsand Asymptotic externalstability.

Apartfromtheuseofthe dominancecorrespondenceinstead oftheweakdominance correspondence, thereare three differencesbetweentheMSSandtheMDS.TherequirementofClosureforMDShasbeenreplacedbyDeterrenceofexternal deviationsinMSS.Since“forevery x

∈

^{M, f}

(

x

) ⊆

^{M”implies“forevery x}

∈

^{M, fN}

(

x

) ⊆

^{M,”thisdifferencereducestothe} use ofthe dominance correspondenceinsteadof theweak dominance correspondence. The second difference is thatthe requirementof Sequentialweak dominancein MDSisbased onthe finitelyiterateddominance correspondence, whereas AsymptoticexternalstabilityinMSSisbasedontheasymptoticdominancecorrespondence.Finally,theMSSisaclosedset bydefinition.

Demuyncketal.(2019) showthefollowingresult.

Theorem4.4.Acoalitionfunctionformgame

(

N

,

v

)

hasauniqueMSS.Ifthecoalitionstructurecoreofthegameisnon-empty,then itisequaltotheMSS.

AsaconsequenceofTheorems3.3,3.5,and4.4,weconcludethattheMDS,thePEMDS,andtheMSScoincidewhenever CSC

= ∅

^{.Example3.6showsthatingeneralMDSandPEMDSarenotthesame.WenextarguethatinExample3.6,theMSS} coincideswiththeMDS.

Example4.5.As in Example 3.6, let

(

N

,

v

)

be the three-player simple majority game, so N

= {

¹

,

2

,

3

}

^{and v}

({

¹

,

2

}) =

v

( {

¹

,

3

} ) =

^v

( {

²

,

3

} ) =

^v

(

N

) =

^{1,whereastheworth ofanyother coalitionisequaltozero.Recall that}M

= {{

¹

,

2

} , {

¹

,

3

} , {

²

,

3

}}

^{isthesetofminimalwinning}coalitions.ItfollowsfromTheorem 4.5inDemuyncketal.(2019) thattheMSSisequal totheset

F

= {

^x

∈

^X

|

P

(

x

) ∩

M

= ∅},

sotheMSScoincideswiththeMDS.

TheequivalenceoftheMSSandtheMDSholdsingeneral;thisisthetopicofthenextsection.

5. Equivalence

BeforeshowingtherelationbetweentheMSSandMDS,we firstintroduceanotherconcept,theweak dominanceMSS, whichresultsfromreplacingthedominancecorrespondenceintheMSSbytheweakdominancecorrespondence.

Definition5.1.Let

(

N

,

v

)

be a coalition function formgame. Theset W

⊆

^{X isa weakdominancemyopicstableset(weak} dominanceMSS)ifitisclosedandsatisfiesthefollowingthreeconditions:

1. Deterrenceofweakexternaldeviations:Foreveryx

∈

^W,g

(

x

) ⊆

^W. 2. Asymptoticweakexternalstability:Forevery x

∈ /

^W,g∞

(

x

) ∩

^W

= ∅

^.

3. Minimality:ThereisnoclosedsetW^{W thatsatisfiesConditions1 and2.}

Theweak dominanceMSShasalsobeenstudiedinDemuyncketal.(2019) anditisexplainedtherehowmostresults establishedfortheMSScarryovertotheweakdominanceMSSforgeneralsocialenvironments.

We show next thatthe concepts ofMSSandweak dominance MSSare equivalent whenapplied to coalitionfunction formgames.

To do so, we need two lemmas first. The first one makes clear that Asymptotic external stability, Asymptotic weak externalstability,andSequentialweakdominanceareequivalent.

Lemma5.2.Let

(

N

,

v

)

beacoalitionfunctionformgame.Foreveryx

∈

^{X itholdsthatf∞}

(

x

) =

^g∞

(

x

) =

^gN

(

x

)

. Proof. Letx

∈

^X.

Lemma 9inKóczyandLauwers(2007) statesthat g^N

(

x

)

isaclosedset,so g^∞

(

x

) =

^gN

(

x

)

. Since f

(

x

) ⊆

^g

(

x

)

,itfollowsimmediatelythat f^∞

(

x

) ⊆

^g∞

(

x

) =

^gN

(

x

)

.

Toshow the reverseinclusion, letsome y

∈

^gN

(

x

)

and

ε >

0 begiven. We havetoshow that there exists

∈

N^and z

∈

^f

(

x

)

suchthatd

(

y

,

z

) < ε

.

Since y

∈

^gN

(

x

)

thereexistsasequenceofoutcomes

(

x⁰

, . . . ,

x

)

suchthatx⁰

=

^x,foreveryk

=

¹

, . . . ,

,x^k

∈

^g

(

x^k−1

)

,and x

=

^y.Fork

=

¹

, . . . ,

,let D^kbethedeviatingcoalitionthatchangestheoutcomefromx^k−1tox^kandP^k

=

^P

(

D^k

,

P

(

x^k−1

))

be the partners’ set of D^k in P(^xk−1

)

. We also define R^k

=

^Pk

\

^{Dk and Ok}

=

^N

\

^{Pk as the setof residual playersand} outsiders,respectively.Wehavethat

u_i

(

x^k

) =

^v

({

ⁱ

}),

ⁱ

∈

^Rk

,

u_i

(

x^k

) =

^ui

(

x^k−1

),

i

∈

^Ok

.

We define W^k

⊂

^{Dk tobe the,possiblyempty, propersubset of Dk consistingofplayersthat onlyweakly improvewhen} movingfromoutcomex^k−1tooutcomex^k,soforevery i

∈

^{Wk itholdsthatu}i

(

x^k−1

) =

^ui

(

x^k

)

.Wedefine

δ =

^min

k∈{1,...,} min

i∈^Dk\^Wku_i

(

x^k

) −

^ui

(

x^k−1

), ε

=

^min

{δ, ε },

so

δ

isthesmallestimprovementofanyofthestrictlyimprovingplayersinvolvedinanymovealongthesequence.Itholds that

δ >

0 andthereforethat

ε

>

0.Fork

∈ {

⁰

, . . . , }

^,define

ν

_k

=

^n2k n²⁺¹

.

We define e

(

W^k

) =

0 if W^k

= ∅

ande

(

W^k

) =

1 otherwise. We usethesequence

(

x⁰

,

x¹

, . . . ,

x

)

ofoutcomesto definea newsequence

(

x⁰

,

x¹

, . . . ,

x

)

ofoutcomesbysettingx⁰

=

^{x0 and,foreveryk}

∈ {

¹

, . . . , }

^,

P

(

x^k

) =

P

(

x^k

),

u_i

(

x^k

) =

⎧ ⎪

⎪ ⎪

⎪ ⎨

⎪ ⎪

⎪ ⎪

⎩

ui

(

x^k

) + ε

ν

k|^Dk\^Wk|

|W^k|

,

i

∈

W^k

,

u_i

(

x^k

) − ε

ν

ke

(

W^k

),

i

∈

^Dk

\

^Wk

,

u_i

(

x^k

) =

^v

( {

ⁱ

} ),

i

∈

^Rk

,

u_i

(

x^k−1

),

i

∈

^Ok

.

Some ofthesedefinitionsneedsomeexplanation.Noticefirstthat thefirstlinedoesnotentailadivision byzero,sinceif i

∈

^{Wk,then Wk}

= ∅

^{.The payoff fortheoutsidersin Ok istheonly onethat directlydependson xk−1 since thatpayoff} cannotbemodifiedbythedeviation.Itisalsodifferentfromu_i

(

x^k−1

)

asitmayhavebeenmodifiedbypreviousdeviations, when,forexample,i

∈

^Wk−1

∩

^Ok.

Compared to the sequence

(

x⁰

,

x¹

, . . . ,

x

)

,the sequence

(

x⁰

,

x¹

, . . . ,

x

)

is such that each strictly improving player in D^k

\

^{Wk donates an amount}

ε

ν

k

/ |

^Wk

|

^{to each of the players in Wk whenever the latter set is non-empty. It is also} importanttoobservethatthefraction

ν

kisann² multipleof

ν

k−¹ andthat

ν

=

¹

/

n.

We showfirst byinduction that,foreveryk

∈ {

⁰

, . . . , }

^,xk

∈

^{X.Obviously,itholds that x0}

=

^x0

∈

^{X.Assume that,for} somek

∈ {

¹

, . . . , }

^,xk−1

∈

^{X.Weshowthatxk}

∈

^{X.Itholdsthat}

ui

(

x^k

) >

ui

(

x^k

) ≥

^v

( {

ⁱ

} ),

i

∈

^Wk

,

ui

(

x^k

) ≥

ui

(

x^k−1

) + δ − ε

ν

_k

>

ui

(

x^k−1

) + δ − ε

≥

ui

(

x^k−1

) ≥

v

({

i

}),

i

∈

D^k

\

W^k

,

ui

(

x^k

) =

v

({

i

}),

i

∈

R^k

,

u_i

(

x^k

) =

^ui

(

x^k−1

) ≥

^v

({

ⁱ

}),

ⁱ

∈

^Ok

,