F U L L L E N G T H P A P E R
Series B
Popular branchings and their dual certificates
Telikepalli Kavitha1·Tamás Király2·Jannik Matuschke3·Ildikó Schlotter4,5· Ulrike Schmidt-Kraepelin6
Received: 30 June 2020 / Accepted: 24 April 2021
© The Author(s) 2021, corrected publication 2021
Abstract
LetGbe a digraph where every node has preferences over its incoming edges. The preferences of a node extend naturally to preferences overbranchings, i.e., directed forests; a branching B ispopularif Bdoes not lose a head-to-head election (where nodes cast votes) against any branching. Such popular branchings have a natural appli- cation in liquid democracy. The popular branching problem is to decide ifGadmits a popular branching or not. We give a characterization of popular branchings in terms ofdual certificatesand use this characterization to design an efficient combinatorial algorithm for the popular branching problem. When preferences are weak rankings, we use our characterization to formulate thepopular branching polytopein the orig- inal space and also show that our algorithm can be modified to compute a branching
A preliminary version of this work has appeared in the proceedings of IPCO 2020.
B
Ulrike Schmidt-Kraepelin u.schmidt-kraepelin@tu-berlin.de Telikepalli Kavithakavitha@tifr.res.in Tamás Király tkiraly@cs.elte.hu Jannik Matuschke
jannik.matuschke@kuleuven.be Ildikó Schlotter
ildi@cs.bme.hu 1 TIFR, Mumbai, India
2 Eötvös University, Budapest, Hungary
3 Research Center for Operations Management, KU Leuven, Leuven, Belgium 4 Centre for Economic and Regional Studies, Budapest, Hungary
5 Budapest University of Technology and Economics, Budapest, Hungary
6 Research Group Efficient Algorithms, Technische Universität Berlin, Berlin, Germany
withleast unpopularity margin. When preferences are strict rankings, we show that
“approximately popular” branchings always exist.
Mathematics Subject Classification 90C27·90C46·68W01
1 Introduction
LetGbe a directed graph where every node has preferences (in partial order) over its incoming edges. We assume thatGcan have parallel edges but no self-loops. In case Gis simple, the preferences can equivalently be defined on in-neighbors. We define a branchingto be a subgraph ofGthat is a directed forest where each node has in-degree at most 1; a node with in-degree 0 is aroot. Thesizeof a branching is the number of edges in it. The problem we consider is to find a branching that ispopular.
Given any pair of branchings, we say a nodeuprefers the branching where it has a more preferred incoming edge (being a root isu’s worst choice). If neither incoming edge is preferred to the other, thenu is indifferent between the two branchings. So any pair of branchings, say B and B, can be compared by asking for the majority opinion, i.e., every node opts for the branching that it prefers, and it abstains if it is indifferent between them. Letφ(B,B)(resp.,φ(B,B)) be the number of nodes that preferB(resp.,B) in theB-vs-Bcomparison. Ifφ(B,B) > φ(B,B), then we say Bismore popularthanB.
Definition 1.1 A branchingBis popular inG, if no branching inGis more popular thanB. That is,φ(B,B)≥φ(B,B)for all branchingsBinG.
An application in computational social choice.We see the main application of popu- lar branchings withinliquid democracy. Suppose there is an election where a specific issue should be decided upon, and there are several proposed alternatives. Every indi- vidual voter has an opinion on these alternatives, but might also consider certain other voters as being better informed than her. Liquid democracy is a novel voting scheme that provides a middle ground between the feasibility of representative democracy and the idealistic appeal of direct democracy [4]: Voters can choose whether they delegate their vote to another, well-informed voter or cast their vote themselves. As the name suggests, voting power flows through the underlying network, or in other words, del- egations are transitive. During the last decade, this idea has been implemented within several online decision platforms such as SovereignandLiquidFeedback1 and was used for internal decision making at Google [23] and political parties, such as the GermanPirate Partyor the Swedish partyDemoex.
In order to circumventdelegation cycles, e.g., a situation in which voterxdelegates to voteryand vice versa, and to enhance the expressiveness of delegation preferences, several authors proposed to let voters declare a set of acceptable representatives [20]
together with a preference relation among them [5,23,31]. A mechanism selects an approved representative for each voter, avoiding delegation cycles. Similarly as sug- gested in [6], we additionally assume voters to accept themselves as their least preferred approved representative.
1 Seewww.democracy.earthandwww.interaktive-demokratie.org, respectively.
This reveals the connection to branchings in simple graphs where nodes correspond to voters and the edge(x,y)indicates that voterxis an approved delegate of votery.2 Every root in the branching casts a weighted vote on behalf of all her descendants. We assume that voters rate branchings only based on their predecessors. This is justified when approved delegates are considered to be more competent both in deciding on the issue as well as in assessing the competence of others. What is a good mechanism to select representatives for voters? A crucial aspect in liquid democracy is thestability of the delegation process [3,14]. For the model described above, we propose popular branchings as a new concept of stability.
Not every directed graph admits a popular branching. Consider the following simple graph on four nodesa,b,c,dwherea,b(similarly,c,d) are each other’s top choices, whilea,c(similarly,b,d) are each other’s second choices. There is no edge between a,d (similarly, b,c). Consider the branching B = {(a,b), (a,c), (c,d)}. A more popular branching is B = {(d,c), (c,a), (a,b)}. Observe thata andcpreferBto B, whiled prefers BtoBandbis indifferent between BandB. We can similarly obtain a branchingB= {(b,a), (b,d), (d,c)}that is more popular thanB. It is easy to check that this instance has no popular branching.
1.1 Our problem and results
The popular branching problem is to decide if a given digraphG admits a popular branching or not, and if so, to find one. We show that determining whether a given branchingBis popular is equivalent to solving a min-cost arborescence problem in an extension ofGwith appropriately defined edge costs (these edge costs are afunction of the branching). The dual LP to this arborescence problem gives rise to a laminar set system that serves as a certificate for the popularity of B, if it is popular. This dual certificate is crucial in devising an algorithm for efficiently solving the popular branching problem.
Theorem 1.2 Given a directed graph G where every node has preferences in arbitrary partial order over its incoming edges, there is a polynomial-time algorithm to decide if G admits a popular branching, and if so, to find one.
The proof of Theorem1.2is presented in Sect.3; it is based on a characterization of popular branchings that we develop in Sect.2. In applications like liquid democracy, it is natural to assume that the preference order of every node is aweak ranking, i.e., a ranking of its incoming edges with possible ties. In this case, the proof of correctness of our popular branching algorithm leads to a formulation of thepopular branching polytopeBG, i.e., the convex hull of incidence vectors of popular branchings inG.
Theorem 1.3 Let G be a digraph on n nodes and m edges where every node has a weak ranking over its incoming edges. The popular branching polytope of G admits a formulation of size O(2n)inRm, and hasΩ(2n)facets.
2 Typically, such a delegation is represented by an edge(y,x); for the sake of consistency with downward edges in a branching, we use(x,y).
Though the above formulation has an exponential number of constraints, it admits an efficient separation oracle. As a consequence, whenGhas edge costs and node pref- erences are weak rankings, the min-cost popular branching problem can be efficiently solved. Thus we can efficiently solve extensions of the popular branching problem where we minimize the largest rank used or allow constraints for forced/forbidden edges when node preferences are weak rankings. In contrast, we show that the min- cost popular branching problem is NP-hard when node preferences are in arbitrary partial order in Section 6.
Relaxing popularity. Since popular branchings need not always exist in G, this motivates relaxing popularity toapproximate popularity—do approximately popular branchings always exist in any instanceG? An approximately popular branchingB may lose an election against another branching, however the extent of this defeat will be bounded. There are two measures of unpopularity:unpopularity factor u(·)and unpopularity marginμ(·), defined as follows:
u(B)= max
φ(B,B)>0
φ(B,B)
φ(B,B) and μ(B)=max
B φ(B,B)−φ(B,B).
A branchingBis popular if and only ifu(B)≤1 orμ(B)=0. We show the following results.
Theorem 1.4 A branching with minimum unpopularity margin in a digraph where every node has a weak ranking over its incoming edges can be efficiently computed. In contrast, when node preferences are in arbitrary partial order, the minimum unpopu- larity margin problem isNP-hard.
Theorem 1.5 Let G be a digraph where every node has a strict ranking over its incom- ing edges. Then there always exists a branching B in G with u(B)≤ logn. Moreover, for every n, we can show an instance Gnon n nodes with strict rankings such that u(B)≥ lognfor every branching B in Gn.
Hardness results for restricted popular branching problems.A natural optimization problem here is to compute a popular branching where no tree is large. In liquid democracy, a large-sized tree shows a high concentration of power in the hands of a single voter, and this is harmful for social welfare [20]. When there is a fixed subset of root nodes in a directed graph, it was shown in [20] that it isNP-hard to find a branching that minimizes the size of the largest tree. To translate this result to popular branchings, we need to allow ties, whereas Theorem1.6below holds even for strict rankings. Another natural restriction is to limit the out-degree of nodes; Theorem1.6 also shows that this variant is computationally hard. The proof of Theorem1.6can be found in the online supplement or in the full version [28] of our paper.
Theorem 1.6 Given a digraph G where each node has a strict ranking over its incom- ing edges, it isNP-hard to decide if there exists
(a) a popular branching in G where each node has at most9descendants;
(b) a popular branching in G with maximum out-degree at most2.
We also consider popularmixed branchingsin the online supplement and in the full version [28]. A mixed branching Pis a probability distribution (or lottery) over branchings inG, i.e.,P = {(B1,p1) . . . , (Bk,pk)}, whereBiis a branching inGfor eachi andk
i=1pi =1,pi ≥0 for alli. The notion of popularity extends naturally to mixed branchings and we show that popular mixed branchings always exist inG;
moreover, a popular mixed branching can be computed in polynomial time.
Background and Related Work.The notion of popularity was introduced by Gärdenfors [19] in 1975 in the domain of bipartite matchings. Algorithmic questions in popular matchings have been well-studied for the last 10-15 years [1,2,8,9,15,16,22,24–27,29, 32]. Algorithms for popular matchings were first studied in theone-sidedpreferences model where vertices on only one side of the bipartite graph have preferences over their neighbors. Popular matchings need not always exist here and there is an efficient algorithm to solve the popular matching problem [1]. The functions unpopularity factor/margin were introduced in [32] to measure theunpopularityof a matching; it was shown in [32] that it isNP-hard to compute a matching that minimizes either of these quantities. In the domain of bipartite matchings withtwo-sidedstrict preferences, popular matchings always exist since stable matchings always exist [18] and every stable matching is popular [19].
The concept of popularity has previously been applied to (undirected) spanning trees [10–12]. In contrast to our setting, voters have rankings over the entire edge set.
This allows for a number of different ways to derive preferences over trees, most of which lead to hardness results.
Techniques.Starting from an LP formulation for determining the unpopularity margin of a given branching, we use LP duality to characterize popular branchings in terms of dual certificates. A dual certificate for a given branching is a family of subsets of the node setV exhibiting a certain combinatorial structure. A certificate of sizek implies that the unpopularity margin of the branching is at most n−k, and thus a certificate of sizenconstitutes a proof that the branching is popular. This is analogous to characterizing popular matchings in bipartite graphs in terms of witnesses (see [15,25,27]). However, such witnesses are points in Rn rather than set families and their structure is far simpler than that of dual certificates for popular branchings.
Our algorithm constructs a partitionXofV such that ifGadmits popular branch- ings, then there has to besomepopular branching inGwith a dual certificate of size nsupported byX(see Sect.3). Moreover, when nodes have weak rankings,Xsup- ports some dual certificate of sizentoeverypopular branching inG: this leads to the formulation of the popular branching polytopeBG (see Sect.6). Our positive results on low unpopularity branchings are extensions of our algorithm (these results are in Sect.4and Sect.5).
Notation.The preferences of nodevon its incoming edges are given by a strict partial order≺v, soe≺v f means thatvprefers edge f to edgee. We usee∼v f to denote thatvis indifferent betweeneand f, that is, neithere≺v f nore v f holds. The relation≺vis aweak rankingif∼v is transitive. In this case,∼v is an equivalence relation and there is a strict order on the equivalence classes. When each equivalence class has size 1, we call it astrict ranking.
2 Dual certificates
We add a dummy noder toG = (VG,EG)as the root and make(r, v)the least preferred incoming edge of any nodevinG. LetD=(V ∪ {r},E)be the resulting graph whereV =VG andE =EG∪ {(r,u):u ∈V}. Anr-arborescenceinDis an out-tree with rootr(throughout the paper, all arborescences are assumed to be rooted atrand to spanV, unless otherwise stated).
Note that there is a one-to-one correspondence between branchings in G and arborescences inD(simply makerthe parent of all roots of the branching). A branch- ing is popular inGif and only if the corresponding arborescence is popular among all arborescences inD.3We will therefore prove our results for arborescences inD.
The corresponding results for branchings inGfollow immediately by projection, i.e., removing noderand its incident edges.
For an arborescence AinD, there is a simple way to check if Ais popular inD.
LetA(v)be the incoming edge ofvinA. Fore=(u, v)inD, define:
cA(e):=
⎧⎪
⎨
⎪⎩
0, ife v A(v), i.e.,vprefersetoA(v);
1, ife∼v A(v), i.e.,vis indifferent betweeneandA(v);
2, ife≺v A(v), i.e.,vprefersA(v)toe.
ForS ⊆E we definecA(S)=
e∈ScA(e). Observe thatcA(A)= |V| =nsince cA(e) = 1 for everye ∈ A. Let Abe any arborescence in D and letΔ(A,A)= φ(A,A)−φ(A,A)be the difference in the number of votes forAand the number of votes for Ain theA-vs-Acomparison. Observe thatcA(A)=Δ(A,A)+n. Since μ(A)=maxA(−Δ(A,A))=maxA(n−cA(A)), we can conclude the following.
Proposition 2.1 Let A be a min-cost arborescence in D with respect to cA. Then μ(A)=n−cA(A). In particular, A is popular in D if and only if it is a min-cost arborescence in D with edge costs given by cA.
Consider the following linear programLP1, which computes a min-cost arbores- cence inD, and its dualLP2. For any non-emptyX ⊆V, letδ−(X)be the set of edges entering the setX in the graphD.
minimize
e∈E
cA(e)·xe (LP1)
subject to
e∈δ−(X)
xe ≥ 1 ∀X⊆V, X = ∅ xe ≥ 0 ∀e∈E.
3 Note that, by the special structure ofD, an arborescence is popular among all arborescences inDif and only if it is a popular branching inD.
maximize
X⊆V,X=∅
yX (LP2)
subject to
X:δ−(X)e
yX ≤ cA(e) ∀e∈E
yX ≥ 0 ∀X ⊆V, X= ∅.
For any feasible solution ytoLP2, letFy := {X ⊆V : yX >0}be the support of y. Inspired by Edmonds’ branching algorithm [13], Fulkerson [17] gave an algorithm to find an optimal solutionytoLP2such thatyis integral. From an alternative proof (Theorem 6.13 in [30]), we get Lemma2.2. A family of setsSis calledlaminarif for any two setsS,S∈Swe have:S⊆SorS⊆SorS∩S= ∅.
Lemma 2.2 There exists an optimal, integral solution y∗ to LP2 such that Fy∗ is laminar.
Letybe an optimal, integral solution toLP2such thatFyis laminar. Note that for any nonemptyX ⊆V, there is ane ∈ A∩δ−(X)and thus yX ≤cA(e)=1. This implies thatyX ∈ {0,1}for allX. We conclude thatFy is a dual certificate for Ain the sense of the following definition.
Definition 2.3 Adual certificate for Ais a laminar familyY ⊆ 2V such that|{X ∈ Y:e∈δ−(X)}| ≤cA(e)for alle∈E.
Lemma 2.4 The following three statements are equivalent:
(1) A is popular.
(2) There exists a dual certificateYfor A with|Y| =n.
(3) There exists a dual certificateY for A with|A∩δ−(X)| =1for all X ∈Y and
|{X ∈Y:e∈δ−(X)}| =1for all e∈ A.
Proof LetYbe a dual certificate for Aof maximum cardinality and observe thatY corresponds to an optimal solution toLP2of value|Y|. Recall from Proposition2.1 that A is popular if and only if it is a min-cost arborescence in D with respect to cA. Hence (1) is equivalent toAcorresponding to an optimal solution toLP1. By LP duality, this is the case if and only ifcA(A)= |Y|, which is equivalent to (2) because cA(A)=nby definition ofcA. Lastly, (3) is equivalent to the characteristic vectors of AandYfulfilling complementary slackness, which is again equivalent toAandY
being optimal solutions.
For the rest of this section, letYbe a dual certificate maximizing|Y|.
Observation 2.5 For everyv∈V we have|{X ∈Y:v∈ X}| ≤2.
Observation2.5is implied by the fact thate=(r, v)is an edge inDfor everyv∈V andcA(e)≤2. For the case whenAis popular, Lemma2.4establishes the following one-to-one correspondence between the nodes inV and the sets ofY: For every set
X ∈Y, there is a unique edge(u, v)∈ Athat entersX. We callvtheentry-pointfor X. Conversely, we letYvbe the unique set inY for whichvis the entry-point; thus Y= {Yv:v∈V}. Laminarity ofYyields the following corollary of Lemma2.4and Observation2.5:
Corollary 2.6 If|Y| =n andw∈Yv\ {v}for somev∈V , then Yw = {w}.
Proof Assume z ∈ Yw \ {w}. By laminarity eitherYw ⊆ Yv holds, in which case z ∈Yw∩Yv∩Yz, a contradiction to Observation2.5, orYv ⊆Ywimplying that the edge from AenteringYw enters two sets fromY, namelyYwandYv, a contradiction to|{X ∈Y:e∈δ−(X)}| =1 for alle∈ A(see Lemma2.4).
The following definition of the set ofsafe edges S(X)with respect to a subset X ⊆V will be useful. LetS(X)be the set of edges(u, v)inE[X] :=E∩(X ×X) such that properties 1. and 2. hold:
1. (u, v)isundominatedinE[X], i.e.,(u, v)⊀v(u, v)∀(u, v)∈E[X].
2. (u, v)dominates(w, v)∀w /∈ X, i.e.,(u, v) v(w, v)∀(w, v)∈δ−(X).
Observation 2.7 If A is popular, then A∩E[X] ⊆S(X)for all X∈Y.
Proof LetX ∈ Ywith|X| >1. By Corollary2.6, for every nodev ∈ X other than the entry-point for X we have{v} =Yv ∈ Y. So any edgee ∈ δ−(v)within E[X] enters exactly one dual set, i.e.,{v}, implyingcA(e) ≥ 1 byLP2. By contrast, any edge (w, v) ∈ E where w /∈ X enters two of the dual sets: X and{v}, yielding cA((w, v))≥2. For the edge(u, v)∈ A∩E[X], these conditions induce exactly the constraints 1. and 2. given above, showing that the edgeA(v)must be safe.
3 Popular branching algorithm
We are now ready to present our algorithm for deciding ifDadmits a popular arbores- cence or not. For eachv ∈ V, step 1 of the algorithm builds the largest setXvsuch thatvcan reach all nodes in Xvusing edges inS(Xv). To construct the setsXv we make use of themonotonicityof S(·), which follows directly from the definition of safe edges:
Observation 3.1 If X ⊆X⊆V , then S(X)⊆S(X).
We will establish later that the collection X = {Xv : v ∈ V} is laminar (see Lemma3.2). In steps 2-3, the algorithm contracts each maximal set inXinto a single node and builds a graphDon these nodes andr. For each contracted setX ∈X, edges leading to nodeXinDcorrespond to undominated edges in Dleading from outside X to thecandidate entry-pointsof X, which are nodes v ∈ X such that X = Xv. Theorems3.3-3.4show thatDadmits a popular arborescence if and only ifDadmits an arborescence.
Our algorithm for computing a popular arborescence in D is given below. An example of the execution of the algorithm is shown in Fig.1.
1. For eachv∈V do:
– letXv0=V andi=0;
– whilevdoes not reach all nodes in the graphDvi =(Xiv,S(Xiv))do:
Xvi+1=the set of nodes reachable fromvinDiv; leti =i+1.
– letXv=Xiv.
2. LetX = {Xv:v∈V},X= {Xv∈X : Xvis⊆-maximal inX},E= ∅.
3. For every edgee=(u, v)inDsuch thatXv∈Xandu∈/ Xvdo:
– ifeis undominated (i.e.,e⊀ve) among all edgese∈δ−(Xv), then f(e)=
(U,Xv) whereu∈UandU∈X, (r,Xv) ifu=r;
– letE:=E {f(e)}.
4. IfD=(X∪ {r},E)contains an arborescenceA, then – letAD = {e: f(e)∈ A};
– letR= {v∈V : vhas an incoming edge in AD};
– for eachv∈ R: letAvbe an arborescence in(Xv,S(Xv))rooted atv;
– return A∗=AD∪v∈R Av.
Else return “No popular arborescence in D”.
Correctness of the above algorithm.We first establish the laminarity of the sets Xu
foru ∈V constructed in step 1 of the algorithm.
Lemma 3.2 X = {Xv:v∈V}is laminar. For anyv∈V , if u∈ Xvthen Xu⊆Xv. Proof We start by proving the second statement. Letv ∈ V andu ∈ Xv. We first show that Xiu ⊆ Xivfor anyi, where we setXvi := Xvwhenever Xivis not defined by the above algorithm. The claim clearly holds fori=0. Letibe the smallest index such thatx ∈ Xui \ Xvi for some nodex; we must havex ∈ Xui−1∩ Xiv−1. By the definition ofXiu,xis reachable fromu inS(Xui−1). Note thatXiu−1⊆ Xiv−1implies S(Xiu−1) ⊆ S(Xvi−1), which yields thatx is reachable fromu inS(Xvi−1)as well.
Moreover,u is reachable fromv inS(Xiv−1)⊇ S(Xv)becauseu ∈ Xv andS(·)is monotone. Hence it follows thatxis reachable fromvinS(Xiv−1)viau, contradicting the assumption thatx ∈/ Xiv. This concludes the proof of the second statement.
Now we will show the laminarity ofX. For contradiction, assume there exists,t ∈ Vsuch thatXs andXtcross, i.e., their intersection is non-empty and neither contains the other. Then, by the second statement of the lemma, neithers∈Xtnort ∈ Xscan hold. So we have thats∈/ Xt andt ∈/ Xs.
Let(x,y)be an edge inS(Xt)such thaty∈ Xs∩Xtbutx∈ Xt \Xs; since each node inXtis reachable fromtinS(Xt), such an edge exists. Sincey∈ Xs\ {s}, there also exists an edge(u,y)in S(Xs). As x ∈/ Xs but(u,y) ∈ S(Xs), we know that
(u,y) y (x,y)which contradicts(x,y)∈S(Xt).
Theorem 3.3 If the above algorithm returns an edge set A∗, then A∗ is a popular arborescence in D.
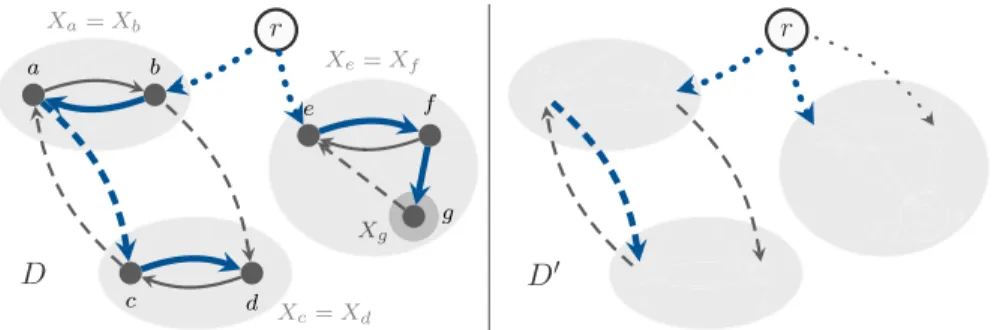
Fig. 1 The left figure shows an example for the graphD, i.e., the input instance extended by a root node r. Some outgoing arcs from the root are omitted inD. Solid arcs are preferred over dashed arcs which are preferred over dotted arcs. Grey areas correspond to sets inX. The right figure depicts the corresponding graphDconstructed by our algorithm. Any arborescence inDcan be extended to a popular arborescence inD. e.g., the arborescence indicated by bold blue arcs is popular
Proof We start by showing that A∗is an arborescence inD. Laminarity ofXimplies that the sets inXare pairwise disjoint. Moreover, by construction, each node inV is included in at least one set in X, namelyv ∈ Xv for each v ∈ V. Hence,X forms a partition ofV. Thus eachw ∈ V has exactly one incoming edge in A∗: an edge from AD ifw ∈ Ror an edge from the arborescence Avfor the unique node v ∈ Rwithw∈ Xvifw∈ V \R. Now assume by contradiction thatA∗contains a cycleC. Because the arborescences Avforv ∈ Rare node-disjoint, this cycle must contain edges from ADand the set{f(e):e∈C∩AD} ⊆Amust contain a cycle, a contradiction. ThusA∗is an arborescence.
We now establish that A∗is popular by showing thatY := {Xv:v ∈ R} ∪ {{v} : v∈ V\R}is a dual certificate for A∗of sizen. Note that|Y| = |R| + |V \R| =n.
We now show that for allv∈V, the incoming edges satisfy the constraints inLP2.
Supposev∈ R. An edge(w, v)∈E enters one set ofYiffw /∈ Xvand no set iff w∈ Xv. Hence, it suffices to show thatcA∗((w, v))∈ {1,2}forw /∈ Xv. Let(u, v) be the incoming edge ofvin arborescenceA∗; note that(u, v)∈ ADandu ∈/ Xv. By construction ofE,(w, v)does not dominate(u, v)and thereforecA∗((w, v))∈ {1,2}.
Supposev ∈V \R. Lets ∈ Rbe the unique node in Rwithv ∈ Xs. Then there is(u, v)∈ As ⊆ S(Xs)by construction of As. Any edge(w, v)∈ δ−(v)enters at most two sets ofY:{v}and possibly Xs. If, on the one hand,(w, v)∈ δ−(Xs), then (u, v)∈S(Xs)dominates(w, v)by property 2. ofS(Xs), and hencecA∗((w, v))=2.
If, on the other hand,w ∈ Xs, then(u, v) ∈ S(Xs)is not dominated by(w, v)by property 1. ofS(Xs), and hencecA∗((w, v))≥1. This proves thatYis a dual certificate
of sizenfor A∗, thusA∗is popular.
Theorem 3.4 If D has a popular arborescence, then our algorithm finds one.
Before we prove Theorem3.4, we need Lemma3.5and Lemma3.6.
Lemma 3.5 Let A be a popular arborescence andY= {Yv:v∈V}a dual certificate for A of size n. Then Yv⊆Xvfor anyv∈V .
Proof Assume for contradiction thatYv\Xv = ∅. BecauseYv ⊆V = X0v, there is an iterationi withYv ⊆ Xvi andYv Xiv+1. Letz ∈Yv\Xvi+1. By Lemma2.4, A entersYvonly atv and thus Acontains a directedv-z-path using only nodes ofYv. Becausez∈/ Xvi+1, there must be an edge(u, w)∈ Aon this path withu∈ Xiv+1and w∈Yv\Xvi+1. Note thatδ+(Xvi+1)∩S(Xiv)= ∅by construction ofXiv+1fromXiv. Thus(u, w) /∈S(Xiv)and one of the following two cases must be true:
Case 1: There exists an edge(x, w) ∈ E[Xiv] that dominates(u, w)and hence cA((x, w))=0. However,{w} ∈Yby Corollary2.6. SoYviolates the dual constraint for(x, w), a contradiction.
Case 2: There is an edge(x, w)∈ δ−(Xiv)which is not dominated by(u, w)and hencecA((x, w))∈ {0,1}. But sincex ∈/ Xiv⊇Yvthe edge(x, w)enters both the set
{w}and the setYvinY, again a contradiction.
Lemma 3.6 Let A be a popular arborescence in D and let X ∈X. Then A enters X exactly once, and it enters X at some nodevsuch that X =Xv.
Proof LetX ∈Xand let Abe a popular arborescence which entersXat some node v∈V through an edge(u, v)∈ A∩δ−(X). Moreover, letYbe a dual certificate for
A, and letYvbe the set whose entry-point isv.
Letentry(X):= {w∈ V :Xw =X}. We first show thatentry(X)⊆Yv. Assume for contradiction that there existsw∈ entry(X)such thatw /∈ Yv. Since Xw = X, we know that there exists aw-v-path P in(X,S(X)). Hence, there exists an edge e = (u, v) ∈ P which enters Yv. Ifv = v, we know thate ∈ S(X)dominates (u, v)∈δ−(X)and hencecA(e)=0, a contradiction to the feasibility ofY. Ifv=v, theneenters not onlyYv∈Y, but also{v} ∈Y. However,cA(e)≤1 sincee∈S(X) must be an undominated edge, a contradiction to the feasibility ofY.
We next show thatv∈entry(X). Lets∈entry(X). By the previous paragraph and Lemma3.5, we gets∈Yv⊆Xv, from which Lemma3.2impliesXs ⊆Xv. Because s∈entry(X), we have X=Xs ⊆Xv. BecauseX ∈Xis inclusionwise maximal in X, we getX =Xv, provingv∈entry(X).
It remains to prove that A enters X only once. Suppose for contradiction that there exist two nodesv, v ∈ entry(X)such that(u, v), (u, v) ∈ A∩δ−(X). By
∅ = entry(X) ⊆ Yv∩Yv and the laminarity of Y, we can assume w.l.o.g. that Yv ⊆Yv. Moreover, sinceu ∈/ X ⊇Yv, the edge(u, v)∈ Aenters bothYvandYv,
contradicting the feasibility of the dual solutionY.
Proof (of Theorem3.4) Assume there exists a popular arborescenceAinD; then there exists a dual certificateY = {Yv : v ∈ V}of sizen for A. We will show that there exists an arborescence inD. By Lemma3.6, for eachX ∈Xthere exists exactly one edgeeX =(u, v)of Athat entersX =Xv.
We claim that(u, v) is not dominated by any (u, v) ∈ δ−(X). Recall that by Lemma3.5, we knowYv⊆Xv=X. If some(u, v)∈δ−(X)dominates(u, v)∈ A, its cost must becA((u, v)) = 0. However,(u, v)clearly enters Yv ⊆ X, andY violates the dual constraint for (u, v), a contradiction. Hence, eX is undominated among the edges ofδ−(X)∩δ−(v)and so our algorithm creates an edge f(eX)in E pointing to X. Using that A is an arborescence in D, it is straightforward to verify that the edges{f(eX): X ∈ X}form an arborescence Ain D. Thus our
algorithm returns an edge set A∗, which by Theorem 3.3 must be a popular
arborescence inD.
Observe that step 1, the bottleneck step, takesO(mn)time per node. An arbores- cence inDcan be found by breadth first search, i.e., in timeO(n+m)wherenand mare the number of vertices and edges inD, respectively. Thus the running time of the algorithm isO(mn2), and Theorem1.2follows.
4 Branchings with minimum unpopularity margin
Recall the definition of theunpopularity marginfor branchings from Sect.1. Again, instead of studying minimum unpopularity margin branchings within the digraphG, we look atr-arborescences of minimum unpopularity margin within the digraphDas constructed in Sect.2. It is easy to see that the unpopularity margin of a branching in G is the same as the unpopularity margin of the corresponding arborescence in D.4 Thus we are looking for an arborescence of minimum unpopularity margin inD. We further obtain the following variant of Lemma2.4which proves useful in bounding the unpopularity margin of a given arborescence inD.
Lemma 4.1 Let A be an arborescence in D andY be a dual certificate for A. Then μ(A)≤n− |Y|, with equality ifYhas maximum cardinality.
Proof LetAbe a min-cost arborescence inDwith respect tocA. Recalling the pair of integral LPsLP1andLP2from Sect.2, we observe thatAcorresponds to an optimal solution toLP1of valuecA(A)andY corresponds to a feasible solution toLP2of value|Y|. We conclude thatcA(A)≥ |Y|by LP duality. Thus, Proposition2.1implies thatμ(A)=n−cA(A)≤n−|Y|. IfYhas maximum cardinality, it is optimal toLP2 and the inequality becomes an equality by strong duality.
4.1 A simple extension of our algorithm: algorithmMinMargin
Our algorithm from Sect.3can be extended to compute an arborescence with mini- mumunpopularity marginwhen nodes have weak rankings. IfDdoes not admit an arborescence, algorithmMinMarginbelow computes a maximum-size branchingB inDand adds edges fromrto all root nodes inBto construct an arborescence. This arborescence inDis then transformed into an arborescence inD. Figure2shows an example execution of the algorithm.
1. LetDbe the graph constructed in the algorithm in Sect.3, and letBbe a branching of maximum size inD.
2. LetBD = {e: f(e)∈ B},R1= {v∈V :δ−(v)∩BD = ∅},R2= ∅.
3. For eachX ∈Xwhich is a root in the branching B, select one arbitraryv ∈ V withXv=X. AddvtoR2and add(r, v)toBD.
4. For eachv∈ R1∪R2, let Avbe an arborescence in(Xv,S(Xv))rooted atv.
4 Note that, due to the special structure ofD, there always exists an arborescence A such that A ∈ arg maxB∈B(D)φ(B,A)−φ(A,B), whereB(D)is the set of branchings inD.
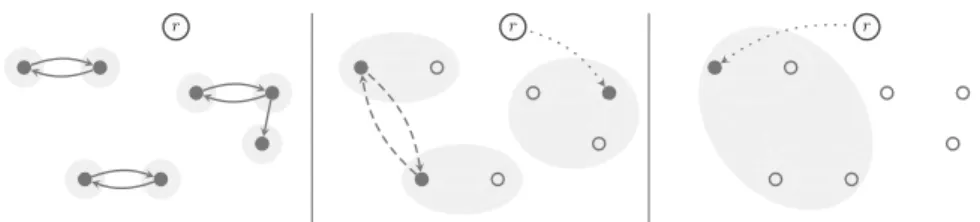
Fig. 2 Variant of the example introduced in Fig.1with one additional incoming arc for nodeb, i.e., the arc (d,b). As a consequence,Ddoes not contain an arborescence. On the right, the bold blue edges form a maximum-size branching inD, which induces an arborescence of minimum unpopularity margin within the graphD. Again, in the left figure, the grey areas correspond to the sets inXand some outgoing arcs of rare omitted (color figure online)
5. Return A∗:=BD v∈R1∪R2 Av.
Theorem 4.2 When nodes have weak rankings, AlgorithmMinMargin returns an arborescence with minimum unpopularity margin in D.
To prove Theorem4.2, we first show in Lemma 4.3that the size of the set R2
is an upper bound on the unpopularity margin of the arborescence A∗ returned by AlgorithmMinMargin. Then we introduce the concept of completeness of dual cer- tificates, which can be used to show that any arborescence in D has unpopularity margin at least|R2|. We remark that only the latter bound requires the properties of weak rankings, whereas the algorithm itself and Lemma4.3hold for arbitrary partial- order preferences.
Lemma 4.3 Let A∗,R2be as computed by the algorithm. Thenμ(A∗)≤ |R2|.
Proof By Lemma4.1it suffices to construct a dual certificate forA∗of sizen− |R2|. DefineY := {Xv : v ∈ R1} ∪ {{v} : v ∈ V \ {R1∪ R2}} and note thatY is a laminar family of sizen− |R2|. It remains to show thatYfulfills the constraints of Definition2.3. To this end, consider any edgee =(w, v)∈ E and let(u, v)be the unique incoming edge ofvinA∗.
Supposev ∈ R2. Thenv is not contained in any set ofY, so the constraint for e=(w, v)is not violated.
Supposev∈ R1. Then(u, v)∈BDandu∈/ Xv. Edgee=(w, v)enters exactly one set ofYifw /∈ Xvand no set ifw∈ Xv. Hence, it suffices to show thatcA∗(e)∈ {1,2}
forw /∈ Xv. Note that(u, v)∈ BD corresponds to an edge in D and henceewith w /∈ Xvdoes not dominate(u, v)by construction ofD. ThuscA∗(e)∈ {1,2}in this case.
Supposev∈V \(R1∪R2). Lets∈ R1∪R2be the unique node in R1∪R2with v∈ Xs. Then(u, v)∈ Asby construction ofA∗. Edgee=(w, v)enters at most two sets ofY ifw /∈ Xs and exactly one set ifw ∈ Xs. Ifw /∈ Xs, then by construction of As and property 2 ofS(Xs), it holds that(w, v)is dominated by(u, v), and hence
cA∗(e)=2. Ifw ∈ Xs, then by construction of As and property 1 of S(Xs),(w, v) does not dominate(u, v), and hencecA∗(e)∈ {1,2}. Thus,Yis a dual certificate for
A∗of sizen− |R2|.
Lemma 4.4 Let A be an arborescence in D. For Z ⊆V andv∈ Z , letYZ,v := {{w} : w∈Z\ {v}} ∪ {Z}. If|{Y ∈YZ,v :e∈δ−(Y)}| ≤cA(e)for all e=(w,x)∈E with x∈Z\ {v}, then Z ⊆Xv.
Proof The proof is a direct analog of the proof of Lemma3.5, withZtaking the role of Yvand noting that this proof only makes use of dual constraints for nodesw∈Yv\{v}.
For Observation 4.5recall that the weakly connected components of a directed graph are the connected components of its induced undirected graph.
Observation 4.5 Let B be a branching of maximum size in D and C ⊆ X be a weakly connected component of Bnot containing r . Then, there exists C ⊆C such thatδ−D(C)= ∅.
Proof Assume for contradiction thatδ−D(C)= ∅for allC⊆C. Hence, everyX∈C is reachable from{r} ∪X\CinD. Consequently, we can modify Bby attaching eachX ∈Cto one of the other connected components ofB, increasing its size by 1.
This contradicts the maximality ofB.
Completeness of dual certificates.LetAbe an arborescence inDandYa dual certifi- cate for A. If an edge(u, v)∈ Aenters a setY ∈Ywe say thatY belongstov. Note that every set ofYbelongs to some node and, sincecA(e)=1 for everye∈ A, at most one set may belong to a node. However, if|Y|<n, the same set ofYmay belong to multiple distinct nodes and there may be nodes to which no set inYbelongs. We say thatYiscomplete on S⊆V, if|{Y ∈Y:Y belongs to somev∈ S}| = |S|. Note that ifYis complete onS, then for eachv ∈Sthere is a unique setYv ∈Ybelonging to v, and for any two distinct nodesv, v∈ Swe haveYv=Yv. In the following proof of Theorem4.2we will show that there exist|R2|disjoint node sets for which no dual certificate of any arborescence can be complete.
Proof (of Theorem4.2) LetAbe an arborescence with minimum unpopularity margin andY a dual certificate for Awith maximum cardinality. We will show that|Y| ≤ n− |R2|. By Lemmas4.1and4.3this impliesμ(A)≥ |R2| ≥μ(A∗), which proves the theorem.
Note that there is a one-to-one correspondence between nodes in R2and the con- nected components ofBinDnot containingr. LetCbe such a connected component.
By Observation4.5, there exists someC ⊆C withδ−D(C)= ∅. We will show that Yis not complete onS:= X∈C X. As the setsSare disjoint for distinct connected componentsC, there exist|R2| pairwise disjoint sets on whichY is not complete.
Since each set ofYbelongs to some node ofV, and at most one set belongs to each node, this implies|Y| ≤n− |R2|.
It remains to show thatYis not complete onS. Assume for contradiction thatYis complete onS and for eachv ∈ SletYvbe the unique set belonging tov. Consider
any edgee=(u, v)∈ A∩δ−D(S)at whichAentersS. We will show thatYv∩Sandv fulfill the requirements of Lemma4.4, but thatYv∩SXv, deriving a contradiction.
ThusYcannot be complete onS.
In the proof of the first claim, we rely on our assumption that the preferences are given by a weak ranking.
Claim LetZ :=Yv∩SandYZ,v := {{w} : w∈ Z\ {v}} ∪ {Z}. Then|{Y ∈YZ,v : e∈δ−(Y)}| ≤cA(e)for alle=(w,x)∈Ewithx∈ Z\ {v}.
Proof of Claim Lete = (w,x) ∈ E withx ∈ Z \ {v}. By the laminarity ofY and its completeness on S, we know that Yx ∩S = {x}. Indeed, assuming thatx is a node inYx ∩S other thanx, the setsYx,Yx, andYvwould necessarily contradict Observation2.5. We distinguish two cases:
Case 1:w /∈ Yv\S. In this caseeentersYvif and only if it entersZ =Yv∩S.
Hence|{Y ∈YZ,v :e∈δ−(Y)}| = |{Y ∈Y :e∈δ−(Y)}| ≤cA(e).
Case 2:w∈Yv\S. In that caseeenters the two setsYv∩Sand{x}. We need to prove cA(e)=2. Consider the setX ∈ Cthat containsx. Note thatδ−D(C)= ∅implies thatemust be dominated by some edge f enteringXatx. Without loss of generality we can choose f such that it is undominated among all edges in δ−D(X)∩δ−D(x). Clearly, f enters the set{x} ∈YZ,v. Note that f cannot enterS, becauseδ−D(C)= ∅ and f is not dominated by edges enteringX ⊆S. So we can apply the statement of the previous case to f, yielding 1≤ |{Y ∈ YZ,v : f ∈δ−(Y)}| ≤ cA(f). This implies that f does not dominateA(x). So eitherA(x) x f x eorA(x)∼x f, which also impliesA(x) x ebecause preferences are weak rankings. HencecA(e)=2.
Claim Yv∩S Xv.
Proof of Claim LetX ∈Xbe the unique set ofXwithv∈X.
Case 1:Xv= X. Lets ∈ V withXs = X. Note thatv ∈ X impliess ∈ X ⊆S.
By construction ofXsthere exists ans-v-pathP⊆S(X)containing only safe edges for Xs. Recall that a safe edge cannot be dominated by any other edge. Ifs ∈/ Yv, then there is an edge(u, v) ∈ P enteringYv. Ifv = v, then the non-dominated edge(u, v)enters two sets ofY, a contradiction. Ifv =v, then(u, v)dominates (u, v)∈ Abut entersYv, again a contradiction. We conclude thats∈Yv. However, as Xv= Xs, we know thats∈/ Xvby Lemma3.2. We obtains∈(Yv∩S)\Xv.
Case 2:Xv=X. Because f(e) /∈δ−D(C)= ∅, there must be an edgee=(u, v) enteringXvatvand dominatinge. Without loss of generality, we can chooseesuch that it is undominated among all edges inδ−D(v)∩δ−D(Xv). Becausee∈ A, we obtain cA(e)=0 and henceecannot enterYv∈Y. We conclude thatu∈(Yv∩S)\Xv.
This completes the proof of Theorem4.2.
4.2 Unpopularity margin under partial preference orders
The following theorem shows that AlgorithmMinMargincannot be extended for the case where each nodevhas an arbitrary partial order overδ−(v).