Napjainkban teljesen magától értetôdônek tûnik, hogy munkánk során számítógépet használunk, internetezünk, bankkártyával fizetünk vagy meghallgatunk egy CD-lemezt. Ilyenkor talán végig sem gondoljuk, hogy ezek egyikét sem tehetnénk meg, ha nem jöttek volna létre a matematika új ágai: az algoritmuselmélet, a kriptográfia vagy a bonyolultságelmélet. Gon- dolnánk-e, hogy adatvédelmünk, a katonai létesítmények, a bankrendszer, s így a gazdaság biztonsága azon is múlik, hogy egy elég nagy szám felbont- ható-e belátható idôn belül prímszámok szorzatára? Miért fontos tudni egy számról, hogy azt véletlen módon adták-e meg nekünk vagy valamilyen al- goritmus eredményeként? Milyen régi problémák megoldásában segíthet nekünk a számítógép s melyekben nem? Ezekre az izgalmas, mindannyiun- kat érintô kérdésekre keresi a választ az elôadás.
Bevezetés
A 20. században az igazi forradalom a számítógépek megjelenésével tört ki.
Az elmúlt évszázad második felét gyakran „atomkorszaknak” nevezik, a
„számítógépek korszaka” elnevezés azonban pontosabb lenne. Akár egy 357
Lovász László matematikus az MTA rendes tagja
1948-ban született. A Fazekas Mihály Gyakorló Gimnázium elsô matematika tagozatos osztályá- ba járt. Szinte minden matemati- ka versenyt megnyert (Ki miben tudós?, KöMaL, OKTV, Nemzet- közi Matematikai Diákolimpia, Schweitzer-verseny stb.). 1971- ben végzett az ELTE Természet- tudományi Karának matematikus szakán. 1970-ben, ötödéves egyetemistaként megvédte a gráfok faktorairól írt kandidátusi disszertációját. Világhírû ered- ménye a perfekt gráfsejtés bizo- nyítása volt. 1979-ben megoldot- ta az információelmélet egyik legnevezetesebb problémáját, a Shannon-problémát. Cikke az év publikációja lett az IEEE Trans- action Information Theorycímû folyóiratban. 1979-ben, harminc- egy éves korában lett az MTA le- velezô, 1985-ben pedig rendes tagja. 1999-ben megkapta a ma- tematikusok Nobel-díjának tar- tott Wolf-díjat.
Pályáját 1971-ben az ELTE tu- dományos fômunkatársaként kezdte, 1982-tôl tanszékvezetô egyetemi tanár, 1987-tôl a Prin- ceton Egyetem, majd a Yale Egyetem egyetemi tanára. Szá- mos nemzetközi tudományos folyóirat – az Acta Mathematica, az Advances in Mathematics szerkesztôbizottságának tagja, aCombinatoricafôszerkesztôje.
Fôbb kutatási területei: kom- binatorika, algoritmuselmélet.
Mit kívánnak a számítógépek
a matematikától,és mit adnak neki?
évig tartó elôadás-sorozatot is össze lehetne állítani arról, hogy a számítógé- pek, az információs technológia milyen hatást gyakoroltak a kultúra és a tudomány különbözô területeire. Ez az elôadás csak a matematika szem- pontjából veszi szemügyre a számítógépeket.
Legjobb, ha mindjárt az elején felhívom a figyelmet arra, hogy a mate- matika az egzakt gondolkodásról szól, és nem lehet a matematikáról anél- kül beszélni, hogy legalább egy kicsit ne kóstoljunk bele ebbe az egzakt gondolkodásba. Elkerülhetetlen tehát, hogy a hallgatókat, olvasókat leg- alábbis idônként arra kérjem, hogy együtt gondolkozzunk, hogy ne csak a tényeket, hanem azok logikáját is kövessék.
Mindjárt fel is teszek egy kérdést, mely gyakran felvetôdik, és melyre az elsô, átgondolatlan válaszunk könnyen az igazság ellenkezôje lehet: Felesle- gessé teszik-e a számítógépek a matematikát?
Minden nagy fejlôdés sok olyan dolgot tesz feleslegessé, mely koráb- ban fontos, sôt alapvetô volt. Odakerül-e a matematika is a logarléc és a gôzmozdony mellé? Látni fogjuk, hogy éppen ellenkezôleg, a számítógé- pek igénye a matematika új fejezeteit hívja létre, és a régi fejezeteket egé- szen új megvilágításba helyezi. A számítógép új kérdéseket tesz fel a mate- matikának, és ezek a kérdések új fogalmak, új paradigmák kialakulásához vezetnek.
A probléma gyakran konkrétabb formában is megfogalmazódik: Nem teszi-e feleslegessé a hardver fejlôdése a matematikai módszereket a programo- zásban? A hardver hihetetlen fejlôdésen ment és megy keresztül. Ezt a fejlô- dést Moore törvényével lehet leírni. Gordon Moore – az Intel egyik alapí- tója – 1965-ben azt a megfigyelést tette, hogy az egy-egy integrált áramkör- ben használt tranzisztorok száma mintegy kétévenként megduplázódik. Ez a gyors fejlôdés azóta is tart.
Sok olyan feladat van, amelyet csak nehezen, bonyolult trükköket be- vetve tudunk megoldani, de alig telik el egy év, és a sokkal gyorsabb, na- gyobb kapacitású gépek játszva megoldják ôket. Úgy tûnhet tehát, hogy kár a bonyolultabb matematikai módszereket erôltetni. Ám ha jobban meg- nézzük, kiderül, hogy éppen ellenkezôleg: a technikai fejlôdés olyan felada- tokat hoz létre, amelyeket „trükkös” gondolkodással már nem lehet megol- dani, csak komoly matematikai módszerekkel.
Meg lehet-e érteni például egzakt matematikai gondolkodás nélkül az internetet, ami több százmillió számítógépet köt össze egymással? Meg le- het-e tervezni egzakt matematikai módszerek nélkül egy modern integrált áramkört, ahol ötvenmillió számítási alapegység van egy négyzetcentimé- teren összezsúfolva? Lehet-e pontos matematikai modellezés nélkül gon- dolkodni egy olyan rendszer biztonságáról, amelyet milliárdnyi ember használ, akiket nem ismerünk – de tudjuk, hogy vannak köztük bûnözôk és terroristák is?
A matematika tehát nagyon is sokat tud nyújtani a számítástechnikának.
De mit kap cserébe? Nagyon sok mindent: izgalmas új fogalmakat, problé- mákat és módszereket, új kísérletezési lehetôségeket. Ezek közül nézünk meg néhányat a következôkben.
358
Eukleidész görög matematikus, Raffaello freskójának részlete
Neumann János alkotta számító- gépben minden egyes rádiócsô egy logikai egység; ma az ábrán látható integrált áramkörökben (amelyek közel mérethûek) akár 50 millió ilyen egység is van
A bonyolultság új fogalma
Abonyolultságfogalma hasonló fejlôdésen ment át az utóbbi ötven évben, mint sok más alapvetô fogalom. Elôször egy megértést akadályozó körül- ményt jelentett (vagy talán csak kényelmes kifogást?). Ha egy jelenség vagy struktúra túl bonyolult, akkor a kutatás során megkerüljük, leegyszerûsít- jük vagy részeire bontjuk. A fogalom történetében az a következô fázis, amikor a tudós elkezdi a bonyolultságot mint önálló jelenséget szemlélni:
kidolgozza, hogyan lehet mérni, szabályokat és törvényeket állapít meg, ezeket kapcsolatba hozza más, korábban megismert dolgokkal. Végül je- lentkezik a mérnök, hogy a bonyolultságot eszközként használja fontos ter- vezési problémák megoldására: az adatvédelem, az elektronikus posta, a ke- reskedelem, a pénzforgalom biztonsága ma nagyrészt a bonyolultság fogal- mán és annak tulajdonságain alapul.
A 19. századi matematika egyik nagy sikere a végtelen fogalmának meg- ragadása volt. Ennek bûvölete olyan erôs, hogy hajlamosak vagyunk min- denre, ami véges, rálegyinteni: „Véges sok eset van, amit végig lehet nézni!”
A számítógépek megjelenése következtében rájöttünk: a véges nagyon nagy lehet, bekövetkezhet az „exponenciális robbanás”.
Exponenciális robbanás
A sakkjáték feltalálójáról szóló klasszikus történet szerint az unalma elûzé- séért hálás király felajánlotta neki, hogy azt kívánhat jutalmul, amit akar.
A feltaláló azt kérte, hogy a sakktábla elsô mezejére tegyenek egy búzasze- met, a másodikra kettôt, a harmadikra négyet, a negyedikre nyolcat és így tovább, minden mezôre kétszer annyit, mint az elôzôre. A király nagyon megörült, hogy ilyen olcsón megúszta, de aztán rá kellett jönnie: nemcsak hogy a 10–12-ik mezôtôl már nem férnek el a búzaszemek, de a tábla köze- pe táján már birodalmának teljes búzatermése sem lett volna elegendô, hogy ígéretét betartsa.
Ezt a jelenséget, hogy ha egy mennyiséget ismételten duplázunk (vagy bármilyen egynél nagyobb számmal szorzunk), akkor igen gyorsan növek- szik, exponenciális robbanásnak hívjuk. Moore említett törvényében az a meglepô, hogy az informatikában bekövetkezett exponenciális robbanás ilyen hosszan tart. Az 1960-as évek környezetvédelmi forradalma azért jött létre, mert egyre többen értették meg: az exponenciális növekedés nem tarthat örökké sem a népesség, sem a termelés, sem a fogyasztás területén.
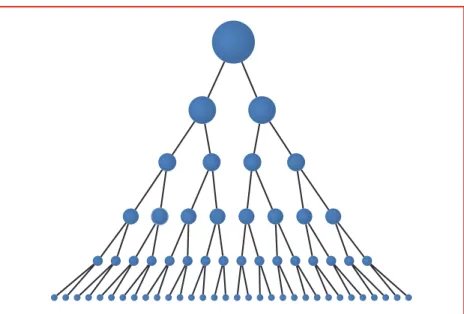
A számítástudományban az exponenciális robbanás leggyakrabban ak- kor lép fel, ha azt a kijelentést, hogy „Véges sok eset van, amit végig lehet nézni!”, megpróbáljuk közelebbrôl is megvizsgálni. Mondjuk, az esetek megkülönböztetéséhez elôször is két alapesetet kell megkülönböztetni; az- tán ezek mindegyikén belül két újabb eset van stb. Ezt a logikai helyzetet egy hálózattal, az ún. bináris fával ábrázolhatjuk (1. ábra). Látható, hogy a végignézendô esetek száma már néhány elágazás után is ugrásszerûen nô, és
bekövetkezik az exponenciális robbanás. Haalgoritmusunknak egy ilyen 359
Sakkozók. Miniatúra a Manesse- féle kéziratból, 14. sz.
Moore-törvény:
Gordon Moore 1965-ben tett megfigyelése, mely szerint egy-egy integrált áramkörben használt tranzisztorok száma mintegy kétévenként meg- duplázódik.
Exponenciális robbanás:
azon jelenség, hogy ha egy mennyiséget ismételten egy 1-nél nagyobb számmal szor- zunk, akkor az igen gyorsan (robbanásszerûen) növekszik.
Bináris fa:
olyan fa (gráf ), melynek min- den ága (éle) tovább ágazik két- felé.
Algoritmus:
egy elvégzendô cselekvésso- rozat megtervezése lépésrôl lépésre.
fát kell végigvizsgálnia, akkor a modern számítógépek – mondjuk – har- minc szint mélységig még bírják, csakhogy minden egyes újabb szint meg- duplázza az esetek számát. Itt még a Moore-törvény sem segít: ha tíz évig várunk, akkor – mondjuk – öt szinttel tudunk továbbmenni.
Ezért aztán a számítástudományban elég hamar megfogalmazódott, hogy olyan algoritmusok tervezésére kell törekedni, melyek lépésszáma a feladat méretével csak mérsékelten nô úgy, mint a méret egy hatványa, nem pedig exponenciálisan. Tehát ha a feladat mérete n,akkor a lépésszám lehet n2vagy n3,de nem lehet 2n.Az ilyen algoritmust polinomiálisnak neve- zik. A kétfajta növekedés közötti különbséget úgy lehet a legjobban szem- léltetni, ha elgondoljuk, mekkora teljesítménynövekedést lehet várni a technológia fejlôdésétôl. Tegyük fel, hogy mind az Aalgoritmus, mind a B algoritmus ma 50 bemenô adattal tud egy adott problémát megoldani. Az Aalgoritmus lépésszáma úgy nô a bemenô adatok számával, mint n3,aB algoritmusé, mint 2n. Ha várunk tíz évet, és a számítógép teljesítménye harminckétszer nagyobb lesz, mint ma (a Moore-törvény szerint), akkor az Aalgoritmus már 150 bemenô adatot tud kezelni, míg a Balgoritmus telje- sítôképessége csak 55 adatra emelkedik.
Prímtesztelés és -faktorizáció
Egy pozitív egész számot prímszámnak nevezünk, ha 1-en és önmagán kí- vül más egész számmal nem osztható. Az 1-et nem tekintjük prímnek, de utána aztán sok példát látunk: 2, 3, 5, 7, 11, 13 stb. Azokat a természetes számokat, melyek nem prímek, fel lehet bontani prímszámok szorzatára, például 6 = 2×3, 40 = 2×2×2×5 stb. – ezt a felbontást nevezzük prímfak- torizációnak.
Aprímszámokkalkapcsolatban két fontos algoritmikus problémát fogal- mazhatunk meg: ha adott egy kjegyû szám, hogyan tudjuk eldönteni róla, hogy prímszám-e; és ha nem prímszám, hogyan tudjuk megtalálni a prím- tényezôit?
360
1. ábra.Bináris fa
Polinomiális algoritmus:
olyan algoritmus, melynek lé- pésszáma a feladat méretével úgy nô, mint a méret egy hat- ványa.
Prímszám:
olyan egész szám, melynek csak az 1 és önmaga az osztója.
Prímfaktorizáció:
a nemprím egész számok (összetett számok) felbontása prímszámok szorzatára. Pél- dául 90 = 2×3×3×5.
Mindkét kérdésre könnyû „véges” választ adni: csak ki kell próbálni, hogy a szám osztható-e a következô számokkal: 2, 3, 4, 5 stb. Ha találunk olyan számot, amelyik osztója, akkor tudjuk, hogy nem prímszám, és a fel- bontást is könnyû elvégezni. A baj ezzel csak az, hogy iszonyú sok számot kell kipróbálni: ahhoz, hogy egy 100 jegyû számról eldöntsük, prím-e: 10100 számot kell kipróbálni, ami nagyobb, mint a világegyetem bármilyen para- métere. Kis odafigyeléssel észrevehetjük, hogy elegendô a szám négyzetgyö- kéig kipróbálni a számokat. De ez sem segít eleget: egy 100 jegyû szám négy- zetgyöke 50 jegyû, és 1050 is messze túl van a lehetôségek határán.
Kiderül, hogy az elsô kérdés sokkal könnyebb, mint a második: olyan hatékony (polinomiális) algoritmusok vannak, amelyek akár 1000 jegyû számról is könnyedén eldöntik, hogy prím-e. A tényezôkre bontásra azon- ban csak olyan algoritmust ismerünk, amely lényegében exponenciális:
100-nál több jegy esetén már csak nagy üggyel-bajjal mûködik, 150 jegy fölött pedig egyáltalában nem. Látni fogjuk, hogy ennek az egyszerû tény- nek hallatlan gyakorlati következményei vannak.
Hogyan lehetséges, hogy a prímfaktorizáció ennyivel nehezebb, mint a prímtesztelés? Azt gondolnánk, hogy mindegyikhez végig kell próbálni az adott számnál kisebb számokat, meg kell gyôzôdni: nem osztható-e velük az adott szám. Nyilvánvaló, hogy ez nagyon hosszadalmas lenne, ezért vala- hogy másképp kell eljárnunk. A hatékony prímtesztelô algoritmusok az ún.
„kis” Fermat-tételen alapulnak (a „kis” jelzô nem a tétel fontosságára utal, azért használjuk, hogy megkülönböztessük a „nagy” Fermat-tételtôl. En- nek bizonyítása sokat váratott magára, amíg Andrew Wiles brit matemati- kus végre megoldotta a problémát. A bizonyítást 1995-ben tette közzé az Annals of Mathematicshasábjain. Pierre de Fermat, a nagy 17. századi fran- cia matematikus csak a „kis tétel” bizonyítását adta meg.)
Fermat tétele szerint, ha pprímszám, és atetszôleges egész szám, akkor p|ap– a
(p osztója az ap– aszámnak). Például, 25–2=30 osztható 5-tel. Ha egy p számról el akarjuk dönteni, hogy prímszám-e, akkor megnézzük, hogy 2p–2, 3p–3 stb. oszthatók-e p-vel. Ellentétben a fenti egyszerû teszttel, ezt nem kell nagyon sok számra kipróbálni, elegendô csak néhányra.
(Sok problémát söpörtem itt a szônyeg alá: néhány pszámra ez a mód- szer hamis pozitív eredményt ad, ezért kicsit módosítani kell; nagy számok nagyon nagy hatványaival kell számolni, ami megoldható, de nem nyil- vánvaló, hogyan stb. De mindezeket megoldva az a teszt, melyet Mil- ler–Rabin-tesztnek neveznek, nagyon jól mûködik.)
A véletlen új fogalma(i)
Avéletlen a modern tudomány egyik sarkalatos fogalma. Szinte minden tu- domány lépten-nyomon használ olyan modelleket, melyekben a jelenségek
véletlen, statisztikus jellege dominál. 361
Ugyanakkor a véletlen igen nehéz fogalom is. Véletlen-e az, hogy egy föl- dobott pénz fejre vagy írásra esik? Ha jól meggondoljuk, miért is ne tudná egy igazán éles szemû és gyors eszû ember az alatt, amíg a pénz fölfelé száll, megfigyelni a pályáját, perdületét és amit csak még kell, és ebbôl kiszámí- tani, hogy melyik oldalára fog esni? A valóságban (talán a kvantumfizikát leszámítva) csupa olyan „véletlen” jelenséggel találkozunk, melyek igazából nem véletlenek, csak prognosztizálásukhoz nem áll rendelkezésre elegendô adat és idô.
Mitôl nem véletlen egy sorozat?
Nézzük a véletlen legegyszerûbb matematikai modelljét. Dobjunk fel egy pénzdarabot – mondjuk – százszor, és írjuk le, hogy fejet vagy írást kapunk.
Valami olyasmit fogunk látni, amit a 2. ábra mutat.
Tényleg véletlen pénzdobálással kaptam ezt a sorozatot? (Nem árulom el.) Ezt a kérdést nem is könnyû eldönteni. Persze ha valami könnyebbet kérdeznék, például a 3. ábrán látható sorozatot, akkor mindenki azonnal látná, hogy ez nem lehet véletlen. Tudjuk, hogy a pénzfeldobásnál ugyan- annyi a fej, mint az írás valószínûsége, ezért egy hosszú pénzfeldobás-soro- zatban körülbelül ugyanannyi fej kell legyen, mint írás.
Nézzünk akkor egy újabb sorozatot! (4. ábra.) Ebben ugyanannyi fej van, mint írás, mégis nyilvánvaló, hogy ez se véletlen. (Érvelhetünk azzal, hogy a páros helyeken is fele-fele arányban kellene fejet és írást látni.)
362
2. ábra.Az érmefeldobások ered- ménye
3. ábra.Hol az érem másik oldala?
Nézzük a következôt! (5. ábra.)
Ez már sokkal kevésbé szabályos, sokkal véletlenszerûbb, de azért gya- nús. Aki jártas a valószínûség-számításban, rögtön látja, hogy túl gyakran váltakozik, nincsen benne például három egyforma érme egymás után. De a legmeggyôzôbb, ha elmondom: a sorozat k-ik eleme , ha a k –1 szám kettes számrendszerbeli alakjában az 1-esek száma páratlan, és , ha pá- ros.Noha a sorozat meglehetôsen szabálytalan, igen egyszerû szabállyal le- írható, tehát egyáltalában nem véletlenszerû.
Nézzünk most egy számsorozatot is! (6. ábra.) Véletlen ez? Gondolom, többen észrevették, hogy ezek egyszerûen a
π
(„pi”) jegyei.363 4. ábra. Ha figyelembe vesszük, hogy az érmének két oldala van…
5. ábra. Vajon véletlen sorozat ez? I.
6. ábra. Vajon véletlen sorozat ez? II.
1 2 7 4 6 2 3 9 4 6 9 7 8 4 1 0 1 4 1 9 2 3 5 6 3 8 4 0 6 5 6 4
3
8
2
0
2
8
4
6
2
8
8
4
8
0
8
3
3
2
5
6
4
8
3
5
9
0
0
1
3
4
9
2
7
5
1
8
0
1
0
7
9
9
5
7
8
2
7
1
8
7
7
0
2
8
4
3
5
2
3
3
6
9
6
2
3
3
9
2
8
7
6
2
5
8
9
9
9
6
0
8
6
3
3
5
9
0
3
5
2
3
9
4
8
7
2
0
9
4
6
4
0
1
8
5
5
6
1
9
2
1
2
5
Még egy sorozatot nézzünk meg! (7. ábra.)
Ez már igazán véletlenszerûnek tûnik! Még a valószínûség-számításban jártas olvasó is nehezen találna kivetnivalót benne. Pedig ez is
π
, csak most 2-es számrendszerben van felírva.Információtartalom és véletlenség
Az elsônek megadott sorozatot (2. ábra) azonban nem tudnám ilyen egy- szerûen leírni, definiálni: igazában semmiféle más értelmes módon nem ír- ható le, csak azzal, hogy felsoroljuk az elemeit. Pontosan ezzel definiálhat- juk a véletlen sorozatot: egy sorozat akkor véletlen, ha nem írható le rövi- debben, mint a saját hossza.
Általánosabban megfogalmazva azt nevezzük egy sorozat vagy bármi- lyen más struktúra, kép stb. információtartalmának (vagy más névenin- formációs bonyolultságának), hogy milyen hosszú a lehetô legrövidebb leírá- sa, mennyire lehet tömöríteni a sorozatot a lehetô leghatékonyabb kódolást használva. (Ez matematikailag pontosan definiálható.)
Ezek után véletlen az a sorozat, melynek az információtartalma a hosszá- nál nem lényegesen kisebb. Megmutatható, hogy az ilyen módon definiált véletlen sorozatokra a valószínûség-számítás alapvetô eredményei, például a nagy számok törvényei érvényesek lesznek.
A 19–20. század fordulóján David Hilbert, a nagy német matematikus megfogalmazta az akkori matematika legfontosabb megoldatlan problé- máit. Ezek egyike a valószínûség fogalmának megalapozása volt. Elôször Richard von Mises tett kísérletet arra, hogy ezt megoldja, olyasformán, ahogyan mi próbáltuk az elôbb: egy fej–írás-sorozatot véletlennek neve- zett, ha a sorozatban közel azonos a fejek és írások gyakorisága, és ez érvé- nyes akkor is, ha csak minden második vagy minden harmadik elemet nézzük stb. Ez azonban nem vezetett sikerre.
Az 1930-as években A. Ny. Kolmogorov – egészen más úton elindulva – az analízis eszközeit (a mértékelméletet) felhasználva alapozta meg a való- színûség fogalmát. Ez matematikailag nagyon jól használható volt, azon- nal elterjedt, és mindenki úgy tekintette, hogy ezzel a probléma meg van oldva. Kivéve magát Kolmogorovot, aki az 1960-as években visszanyúlt von Mises kísérletéhez, és azt úgy fejlesztette tovább, hogy matematikai-
364
Információtartalom:
egy sorozat vagy egyéb struktú- ra információtartalma az, hogy milyen hosszú a lehetô legrövi- debb leírása a lehetô leghatéko- nyabb kódolást használva.
7. ábra. Vajon véletlen sorozat ez? III.
Hilbert, David (1862–1943)
lag használható lett. Ezzel nagy lépést tett a véletlen nehéz fogalmának megértése felé.
Egy sorozat információtartalmának a definíciója a valószínûség fogal- mától függetlenül is sok izgalmas megoldatlan kérdéshez vezet: Mekkora a genetikus kód, például egy emberi kromoszóma információtartalma? Mek- kora az agy bonyolultsága? Milyen nagyságrendû az egész világegyetem bo- nyolultsága?
Véletlen és álvéletlen
Van azonban a bonyolultság fogalmának egy hátránya is: egy sorozat bo- nyolultságát nem lehet semmilyen algoritmussal sem kiszámítani. Továbbá, ilyen értelemben véletlen számokat számítógéppel generálni fából vaska- rika, hiszen egy számítógéppel generált sorozat információtartalma csak annyi, mint az ôt generáló program információtartalma, ami a sorozat hosszától függetlenül korlátos.
Mivel azonban számítógép által generált véletlen számokra szükség van, egy másik fogalommal kell dolgozni. A bonyolultságelmélet segítségével két új kritériumot kaphatunk arra a kérdésre, hogy mikor tekinthetünk egy sorozatot véletlennek.
1. Képzeljük el, hogy két gépünk van, melyek mindegyike 0-kat és 1-eseket nyomtat egy papírra. Az egyik gépben egy igazi véletlent elôállító fizikai eszköz van, és a kiadott sorozat egymástól független bitekbôl áll, me- lyek 1 valószínûséggel lehetnek 0 vagy 1. A másik gépben egy program gyártja a számokat egy rövid „magból”, azaz egy olyan számból, amely a ge- neráló algoritmus kiinduló (inicializáló) értéke. A programot ismerjük, a magról azonban csak annyit tudunk, hogy hány jegyû. A legfontosabb:
nem tudjuk, melyik gép melyik. A feladatunk, hogy ezt megtippeljük.
(Elôfordulhat, hogy a valódi véletlent adó gép véletlenül olyan sorozatot állít elô, melyet az álvéletlent adó gép is elôállíthat. Ebben az esetben nem tudunk biztos választ adni. Ennek azonban igen kicsi a valószínûsége.)
Ha korlátlan idô állna rendelkezésre, akkor könnyû volna igen jó eséllyel tippelni: egyszerûen kipróbálnánk minden egyes magot, hogy abból indul- va melyik generátor produkálja a megfigyelt sorozatot. Ehhez azonban 2n sorozatot kell kipróbálnunk. Így ezt a túl könnyû megoldást kizárhatjuk az- zal, hogy csak polinomiális algoritmust engedünk meg.
Egy másik triviális, érdektelen megoldás az volna, ha úgy tippelnénk meg, melyik sorozat az igazi véletlen, hogy feldobunk egy forintot. Az ese- tek felében ez jó eredményt ad. Ahhoz, hogy ezt kizárjuk, megköveteljük, hogy a felismerô algoritmus az esetek több mint felében adjon jó ered- ményt. Pontosabban azt követeljük meg, hogy annak a valószínûsége, hogy az algoritmus helyesen tippeli meg, hogy melyik sorozat a véletlen, legalább 51 százalék legyen.
Akkor mondjuk tehát, hogy a generátor az igazitól megkülönböztethetet- len,ha nincs olyan algoritmus, mely polinomiális idôben az esetek 51 szá- zalékában helyesen tippeli meg, hogy melyik gép az, amelyik a valódi vélet-
len sorozatot adja. 365
Álvéletlen számok:
algoritmussal elôállított kel- lôen bonyolult számsorozat, amely a véletlen számsorozat bizonyos jegyeit viseli magán.
2. Képzeljük el, hogy csak egy gépünk van, melyrôl tudjuk, hogy álvélet- len-sorozatot állít elô ismert programmal, de a magról ismét csak azt tud- juk, hogy milyen hosszú. Megfigyeljük a kijövô sorozatot, de mielôtt egy- egy újabb jegyét megnéznénk, megpróbáljuk megtippelni, hogy mi lesz a következô. Az elôzôekhez hasonlóan a tippeléshez csak polinomiális idôt használhatunk, és annyit kell elérnünk, hogy az esetek 51 százalékában sikeresen tippeljünk. Ha nincs ilyen algoritmus, akkor azt mondjuk, hogy a generátor megjósolhatatlan.
Ez a két definíció ekvivalens: ha egy álvéletlen-sorozat az igazitól megkü- lönböztethetetlen, akkor megjósolhatatlan – és viszont. Ez egyáltalában nem nyilvánvaló.
Még kevésbé nyilvánvaló az, hogy létezik elméletileg is jó generátor – ennek a kérdésnek a tárgyalása azonban nem fér bele ebbe az elôadás- ba. Annyit mégis meg szeretnék jegyezni: ez is azon alapszik, hogy míg két számot könnyû összeszorozni, nem könnyû egy számot tényezôire bontani.
Ezeknek az eredményeknek filozófiai tartalma is van. Van-e értelme va- lamit „kiszámíthatónak”, „determináltnak” nevezni, ha csak „elvileg” szá- mítható ki, ami azt jelenti, hogy a számítás a világ végezetéig tartana?
A bizonyítás új fogalma
A bizonyítás a matematika lelke, a görög tudomány talán legfontosabb alkotása. Mégis, az iskolai matematikatanításból sokszor kimarad. Még egye- temi hallgatók is gyakran nem értik, miért van rá szükség: „Elhisszük mi a tanár úrnak, minek azt bizonygatni.”’ (Remélem, ez csak amerikai tapasz- talatom, Magyarországon nem így van.)
A Pitagorasz-tételre már nagyon-nagyon sok bizonyítást talált az embe- riség, és világos, hogy a bizonyításon nem azért kell végigmenni, hogy a té- tel helyességérôl még jobban meg legyünk gyôzve, hanem azért, hogy a bi- zonyításban szereplô matematikai módszereket elsajátítsuk. A programok helyessége, a kommunikációs protokollok biztonsága azonban nap mint nap bizonyítást igényel(ne).
Interaktív bizonyítás
Még érdekesebb azonban, hogy az informatika a bizonyítás újszerû fogal- mához is elvezet: az interaktív bizonyításhoz.
Alan M. Turing angol matematikus, a számítógép-tudomány egyik megalkotója azon gondolkodott, hogy vajon hogyan lehet megkülönböz- tetni egy nagyon fejlett számítógépet egy embertôl. Azt a kísérletet javasol- ta, hogy egy szobába ültessünk be egy embert egy képernyôvel és billentyû- zettel, míg a másik szobába vagy egy másik embert ültessünk hasonló kép- ernyôvel és billentyûzettel, vagy egy számítógépet tegyünk. Az elsô ember kérdéseket tehet fel, vagy bármi egyéb módon társaloghat a másik szobában
366
Püthagorasz görög matematikus, Raffaello freskójának részlete
Véletlenszám-generátor:
álvéletlen-számsorozatot elô- állító algoritmus.
levô lénnyel, és el kell döntenie ennek alapján, hogy emberrel vagy géppel áll-e szemben. Ezt a kísérletet nevezik Turing-tesztnek.
Hinnénk-e, hogy ezt a nyilvánvalóan csak gondolatkísérletnek szánt tesztet naponta sok ezerszer végzik el? Ha valaki például új elektromos postafiókot akar nyitni, ilyesféle kérdéssel találkozhat: „Kérjük, gépelje be az alábbi betûket”, és szürkés, kicsit piszkosnak tûnô alapon néhány kuszán odaírt betût lát. (8. ábra.)
Ha valaki nem érti, mire való ez, rákattinthat a „Miért?” feliratra, és megtudja, hogy azért van erre szükség, mert sok program van, ami automa- tizálja a címek létrehozását, hogy aztán hirdetéseket küldjön szét róluk, vagy ami rosszabb, levelek tömeges küldésével megbénítson valakit. A ké- pen az emberi szem könnyedén felismeri a betûket, de egy számítógépet (ma még legalábbis) a betûk torzulásai és a kusza vonalak megtévesztenek, így a programozott címgenerálást ki lehet szûrni.
Látszik tehát, hogy a mai számítógépek még nagyon gyorsan megbuk- nak a Turing-teszten, bár érdemes azt is megemlíteni, hogy itt a tesztet ma- gát nem ember, hanem egy számítógép hajtja végre.
A fenti eljárás az interaktív bizonyítás szép példája: két résztvevô van, és ebben az esetben a Bizonyító azt a „tételt” akarja bebizonyítani, hogy ô em- ber. A hagyományos matematikában a tételhez hozzá lehet csatolni a bizo- nyítást – itt azonban van egy Ellenôr, aki egy vagy több kérdést tesz föl, és a
„bizonyítás” a kérdéstôl függ. Ez a séma sokkal erôsebb a hagyományos bi- zonyítási formáknál – gondoljunk csak bele, hogyan tudnánk kérdés nélkül bebizonyítani, hogy emberek vagyunk.
Érdemes azt is megjegyezni, hogy a séma ereje a kérdés (a kusza betûso- rozat) véletlen voltán múlik. Ha mindenkitôl ugyanazt kérdezné vagy akár csak elôre kiszámítható kérdést tenne fel, könnyû volna egy számítógépet úgy programozni, hogy az a jó választ adja. A jó véletlen-generátor tehát ennek a protokollnak is elengedhetetlen része!
Elektronikus boríték
Hasonló interaktív bizonyítások lépten-nyomon elôfordulnak – gondol- junk a jelszavakra, az „okos kártyákra” stb. Számítógépes hálózataink biz- tonsága nagyrészt az ilyen bizonyításokon múlik. Hadd mutassak be egy nagyon leegyszerûsített példát. Tegyük fel, hogy Aliz és Béla interneten ke- resztül sakkozik. Beesteledett, és meg kell szakítani a mérkôzést. Hagyomá- nyos sakkversenyen ilyenkor az történik, hogy – mondjuk – Aliz eldönti az utolsó lépést, de nem teszi meg a táblán, hanem borítékolja és odaadja a bí-
rónak. A borítékot Béla csak másnap nyithatja ki. Így egyikük sem ismeri a 367
8. ábra.Kérjük, gépelje be az alábbi karaktereket
Turing-teszt:
gondolatkísérlet, mely azt hiva- tott eldönteni, hogyan lehet egy nagyon fejlett számítógépet megkülönböztetni egy ember- tôl.
másik utolsó lépését, ezért nincs az a nagy elônye, hogy egész éjjel gondol- kodhat a lépésén.
De most nincs bíró és nincs boríték. Aliz üzenhet valamit Bélának este, és megmondhatja a lépését másnap reggel. De mit üzenjen este? Ha már esti üzenetével elkötelezi magát, akkor Béla elônyben lesz; ha nem, akkor Aliz lesz elônyben, mert megváltoztathatja a lépést az éjszaka folyamán.
A hagyományos információelmélet szerint a „borítékolás” lehetetlen.
A bonyolultságelmélet azonban megoldást kínál. Elôre megállapodnak abban, hogy a lépéseket egy-egy négyjegyû számmal írják le: például Kf3 helyett azt mondják, hogy 9083. Ezek után Aliz választ magának két 100 jegyû prímszámot, amelyek közül a kisebbik úgy kezdôdik, hogy 9083…
(Láttuk, hogy számítógéppel nem nehéz ellenôrizni, hogy egy szám prím- szám-e; be lehet bizonyítani a klasszikus matematika mély eszközeit fel- használva, hogy ha néhány száz 100 jegyû számot találomra kipróbál, ezek között nagy valószínûséggel lesz prím.) Legyen ez a két szám p és q, ahol p<q. Este Aliz elküldi a pqszorzatot Bélának, reggel pedig elküldi a két té- nyezôt (ami a boríték felbontásának felel meg).
Láthatjuk, hogy Béla már elôzô este megkapta a teljes információt: egy körülbelül 200 jegyû természetes számot, melynek a kisebbik prímtényezô- jébôl az elsô 4 jegy megadja Aliz lépését. De mivel a számot nem tudja haté- konyan tényezôire bontani, a lépést másnap reggelig (vagy akár évekig) nem tudja kiolvasni. Ezt a „titkot” hétpecsétként ôrzi a számítási bonyo- lultság.
(Egyébként Béla jól teszi, ha ellenôrzi, hogy pés qtényleg prímek. Aki szeret logikai feladatokon eltöprengeni, elgondolkodhat, miért van erre szükség.)
Ennél sokkal bonyolultabb módon – de azért hasonló gondolatokat használva – lehet digitálisan létrehozni a társadalmi érintkezés olyan fontos elemeit, mint a mások által felbonthatatlan boríték (titkosírás), elismer- vény, számla, aláírás és annak hitelesítése, vízjel stb.
Klasszikus kérdések új megvilágításban
A klasszikus matematikát sokan elefántcsonttoronynak látják. Godfrey H. Hardy, aki a prímszámok elméletének egyik legkiemelkedôbb kutatója volt a 20. század elsô felében, ezt írja Egy matematikus védekezése (A mathe- matician’s apology)címû könyvében:
Soha nem tettem semmi „hasznosat”. Semelyik felfedezésem sem volt közvet- lenül vagy közvetve jó vagy rossz hatással a világ folyására, és nem valószínû, hogy valaha is hatással lesz…
Az „igazi” matematikusok „igazi” matematikája – Fermat és Euler és Gauss és Abel és Riemann matematikája – csaknem teljesen „haszontalan’’.
368
Euler, Leonhard svájci matematikus (1707–1783)
Gauss, K. F. német matematikus (1777–1855)
Amikor az interneten vásárolunk vagy bankügyeket intézünk, számító- gépünknek több száz jegyû számokról kell eldöntenie, hogy prímek-e – tized- másodpercek alatt. Ehhez Fermat tételét használja. A különbözô számító- gépes protokollok, biztonsági módszerek a Hardy által felsorolt nagyságok szinte mindegyikének a munkájára építenek.
Ha azt kérdezzük, melyik az a megoldatlan matematikai probléma, amelynek a legnagyobb a gyakorlati jelentôsége, szerintem egyértelmû a vá- lasz: Fel lehet-e egy – mondjuk – 1000 jegyû számot hatékonyan (nem csillagá- szati idô alatt) prímtényezôire bontani?
Azt hiszem azonban, hogy ezek a tények Hardy kutatási elveit legalább annyira alátámasztják, mint amennyire az állításait cáfolják. Ha ezeket a nagyságokat csak kutatásuk közvetlen haszna motiválta volna – és nem a matematikai kérdések szépsége, a megismerés vágya –, akkor ma nem len- nének eszközeink a számítógép-rendszerek biztonságának védelmére.
369 Abel, N. H. norvég matematikus (1802–1829)
370
Aho, Alfred V. – Hopcroft, John E. – Ullman, Jeffrey D.:
Számítógép-algoritmusok tervezése és analízise. Bp.:
Mûszaki Kvk., 1982.
Gács Péter – Lovász László:Algoritmusok. Bp.: Mûszaki Kvk., 1978.; Tankönyvkiadó, 1987.
Goldreich, Oded:Modern Cryptography, Probabilistic Proofs and Pseudorandomness. In: Algorithms and Combinatorics, Vol 17, Springer-Verlag, 1998.
Lovász László:Algoritmusok bonyolultsága. ELTE egyetemi jegyzet. Bp.: Tankönyvkiadó, 1989.
Lovász László:Egységes tudomány-e a matematika?
Természet Világa,Matematika különszám, 1998.
Lovász László:Véletlen és álvéletlen. Természet Világa, Informatika különszám, 2000.
Lovász, László:Information and complexity (how to measure them?) In: The Emergence of Complexity in Mathematics, Physics, Chemistry and Biology (ed.
B. Pullman), Pontifical Academy of Sciences, Vatican City. Princeton University Press, 1996. 65–80. p.
Luby, Michael:Pseudorandomness and Cryptographic Applications. Princeton, NJ: Princeton University Press, 1996.
Rónyai Lajos – Ivanyos Gábor – Szabó Réka:Algoritmusok.
Bp.: Typotex, 1998.