Tartószerkezetek biztonsága, tőzvédelmi felületkezelési módszerek

Tartószerkezetek biztonsága,

tőzvédelmi felületkezelési módszerek

Szerzık: Dr. Jármai Károly, egyetemi tanár Dr. Farkas József, prof. emeritusz

Lektor: Dr. Orbán Ferenc

Tartalomjegyzék

___________________________________________________________________________

Tartalomjegyzék ………2

Jelölésjegyzék ………3

Bevezetés ………...9

1 Az optimális méretezés újabb módszerei ………12

2 Költségszámítások ………26

3 Stabilitás ………40

4 Egyirányban nyomott, kétirányban bordázott lemez optimálása minimális költségre …….58

5 Nem egyenletesen győrőbordázott külsı nyomással terhelt kúphéj optimális méretezése költségminimumra ………...……….67

6 Hegesztett szerkezetek tervezése tőzvédelemre ………73

7 Tartály alátámasztó acélkeret optimálása tőzvédelemre ………...88

8 Épület acélkeretének optimálása tőzvédelemre ………..100

9 Tőzvédı bevonatok, borítások alkalmazása ………110

10 Animáció az optimálásra ………..116

Jelölésjegyzék

___________________________________________________________________________

•

a, ax, ay a bordák távolsága [mm],

ae, afc, agc idıparaméterek, atc, asp, idıparaméterek,

aw varratméret

[mm],

A keresztmetszet-terület

[mm²],

Af övlemezterület

[mm²],

Ap lemezegyengetés területe

[m²],

As felület

[m²],

Aw gerinclemez-terület

[mm²],

b, b₀ lemezszélesség [mm],

be együttdolgozó lemezszélesség

[mm],

bf övlemezszélesség

[mm],

b_e , b_fc idıparaméterek,

bx,, by a négyszöglemez befoglaló méretei [mm],

B hajlítási merevség

[Nmm²],

Bx, By ortotróp lemez hajlítási merevsége

[Nmm²],

Bxy , Byx csavarási merevség [Nmm²],

c* megengedett lehajlás-arány,

c1, c2, c3 állandók, hegesztési költségek számításához, Ce, Cf, Ch állandók,

Cw lehajlási állandó,

D átmérı [mm],

e,e₁,e₂ távolságok, excentricitások

[mm],

E rugalmassági modulusz

[GPa],

E1= E/(1- ν2) lemezek rugalmassági modulusza [GPa],

EA, ES Al-ötvözetek és acélok rugalmassági modulusza [GPa],

fy folyáshatár

[MPa],

F erı

[N],

gj egyenlıtlenségi feltételi függvények,

G tömeg,

G állandó terhelés,

GAl, GS Al-ötvözetek és acélok tömege [kg],

G nyírási modulusz

[GPa],

h magasság

[mm],

hk egyenlıségi feltételi függvények,

H ortotróp lemez csavarási merevsége

[Nmm²],

i index,

i_u = −1 imaginárius egység,

I egységmátrix,

Ix, Iy inercianyomaték [mm⁴],

It csavarási állandó

[mm⁴],

j index,

km , kf fajlagos anyag- és gyártási költségtényezık, [$/kg,

$/óra],

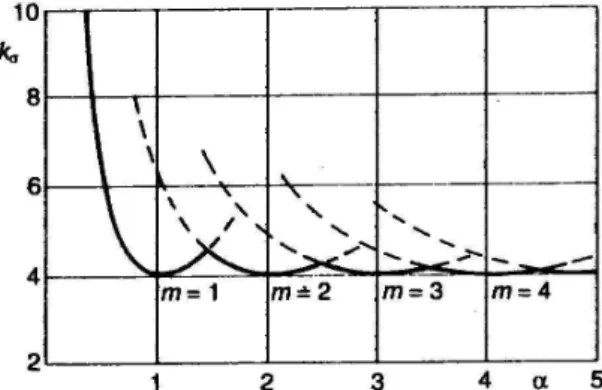
k_σ,k_τ horpadási tényezı,

K költség

[$],

Km, Kf anyag- és gyártási költségtényezık, [$],

l index,

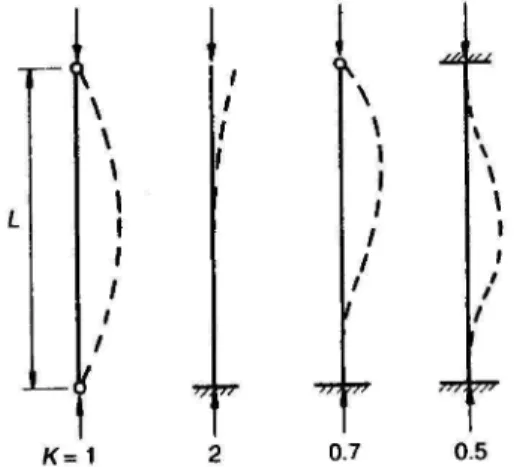
L feltáv, hosszúság

[m],

Lw hegesztési hossz

[mm],

m tömeg

[kg],

mx, my egységnyi hosszra esı hajlítónyomaték

[Nm/m],

mxy egységnyi hosszra esı csavarónyomaték [Nm/m],

M hajlítónyomaték

[Nm],

Mp hajlítónyomaték képlékenységi határa [Nm],

Mt csavarási nyomaték

[Nm],

N axiális erı

[N],

p egyenletesen megoszló terhelés

[N/m],

Q változó terhelés,

r inerciasugár

[mm],

rk büntetıfüggvény együtthatója,

S statikai nyomaték,

S_i lépéstávolság,

t vastagság

[mm],

to megadott minimális lemezvastagság

[mm],

tf, tw övlemez- és gerinclemez vastagság [mm],

tr, t^S bordavastagság

[mm],

T1, T2, T3 idı, gyártási idık [s],

V térfogat

[mm3],

V nyíróerı [N],

w lehajlás

[mm],

w* megengedett lehajlás

[mm],

W, Wx rugalmas keresztmetszeti tényezı

[mm3],

Wp képlékeny keresztmetszeti tényezı [mm3],

Wo szükséges keresztmetszeti tényezı [mm3],

x koordináta,

xi, x1, x2 független változó,

y koordináta,

z koordináta,

α hajlásszög,

α ^{= a/h} paraméter,

β határkarcsúság,

β konvergencia paraméter,

γS biztonsági tényezı,

δ határ övlemezkarcsúság,

δ_{c = D/t} átmérı/vastagság arány körcsıszelvényeknél,

ε fajlagos nyúlás,

ε = 235/ f_y;ε = 250/ p₀ módosító tényezı acél és Al-öntvényekre, ε_y folyáshatárhoz tartozó fajlagos nyúlás,

ζ paraméter,

η _{= by/t} paraméter,

κ szerkezeti elemek száma hegesztéshez való összeszerelésnél, ϑ=100D/L paraméter körcsı szelvényekre,

ϑ = a/tf paraméter,

ϑS = b/t lemeskarcsúság,

Θd gyártási nehézségi tényezı,

λ oszlop karcsúsági tényezıje,

λ redukált karcsúsági tényezı,

λⁱ optimális lépéstávolság,

λp oszlop karcsúsági arány,

µ paraméter,

υ Poisson tényezı,

ρ anyagsőrőség

[kg/m³],

σ normál feszültség

[MPa],

σe külsı terhelésbıl származó húzófeszültség

[MPa],

σadm megengedett normálfeszültség [MPa],

∆σN fáradási feszültségtartomány [MPa],

τ nyírófeszültség

[MPa],

ϕ paraméter,

ξ = x L/ változó,

χ kihajlási tényezı,

ψd dinamikus tényezı,

ψe együttdolgozó lemezszélességi tényezı,

Matematikai szimbólumok

∂

∂ parciális derivált,

∆ derivált, vagy lépés távolság,

∇ második derivált,

∞ ^végtelen,

∈ tartomány eleme,

∑ összeg,

∏ produktum.

Rövidítések

CHS körcsıszelvényő rúd (Circular Hollow Section), EC3 Eurocode 3,

RHS négyszögcsıszelvényő rúd (Rectangular Hollow Section), SHS négyszögcsı-szelvényő rúd (Square Hollow Section).

Bevezetés

Acélszerkezeteknél tömeg- és költségcsökkentés leghatékonyabb módszere a lemezvastagságok csökkentése. Ez vékonyfalú hegesztett szerkezetekhez vezet, amelyek tervezése során számos szempontot kell figyelembe venni: a varratok zsugorodása maradó feszültségeket és vetemedéseket okoz, a vékony lemezek és héjak horpadhatnak, berezeghetnek, zajosak lehetnek, rezgéscsillapítást igényelnek, a nagy feszültségcsúcsok fáradási töréshez vezethetnek, a vékonyfalú szelvények érzékenyek a gátolt csavarásra.

E jelenségek kiküszöbölésére a lemezeket és héjakat bordázással kell ellátni. A szükséges minimális lemezvastagságokat optimális méretezéssel kell kiszámítani.

A tervezés alapja a szerkezeti jellemzık elemzése.

Szerkezet-jellemzık

(a) Terhelések: állandó, változó – statikus, dinamikus (fárasztó, ütı), megoszló – koncentrált, hidrosztatikus, belsı – külsı nyomás, síkbeli - térbeli, önsúly, hasznos teher, hó, szél, hı, földrengés,

(b) Igénybevételek: húzás, nyomás, hajlítás, nyírás, csavarás,

(c) Anyagok: normál- és nagyszilárdságú acél, rozsdamentes acél, idıjárásálló acél, acélöntvények, alumínium-ötvözetek, kombinációk vasbetonnal, szálerısítéses mőanyaggal, gumi,

(d) Tönkremeneteli módok: szakadás, elnyíródás, instabilitás (kihajlás, horpadás, kifordulás), megfolyás, nagy alakváltozások, rideg törés, fáradás,

(e) Szerkezettípusok: rúdszerkezetek: két- és többtámaszú tartók, rácsos tartók, keretek – felületszerkezetek: lemezek és héjak, kötélszerkezetek,

(f) Kötéstípusok: szegecselt, hegesztett, csavarozott, ragasztott, kombinált, (g) Geometria, topológia, peremfeltételek: fı méretek, hajlásszögek, terhelés-

támadáspontok, megtámasztások (csukló, befogás, görgıs támasz, villás támasz, szabad szegély), rudak száma és helyzete rácsos tartókban és keretekben, lemezek alaprajza, héjak alakja,

(h) Szelvényprofilok: hengerelt, hegesztett, sajtolt (alumínium) , ragasztott (réteges, szendvics), csı (üreges) szelvények,

(i) Felületkezelés, felületvédelem: festés, tőzi horganyozás, bevonatok, tőzvédelem, üreges szelvények kitöltése,

(j) Szállítás, szerelés: szállítható egységek a szállítás módjától függıen,

(k) Költségek: tervezés, anyagok (rudak, lemezek), gyártás: összeállítás, hegesztés, bevonatok.

A szerkezet-jellemzıket részletesen az egyes szerkezeteknél tárgyaljuk.

Az optimális méretezés rendszere

Az optimálás jobb megoldások keresése, amelyek jobban megfelelnek a követelményeknek.

A teherviselı mérnöki szerkezetek fı követelményei: terhelhetıség (biztonság), gyárthatóság és gazdaságosság.

Az elemzés szintjén meg kell fogalmazni a tervezési és gyártási feltételeket, valamint a költségfüggvényt. Elemezni kell a vizsgált szerkezettípus szerkezet-jellemzıit és ki kell választani azokat a paramétereket (változókat), amelyek változtatásával jobb megoldások érhetık el.

Az optimálás (szintézis) szintjén minimálni kell a költségfüggvényt a tervezési és gyártási feltételek (korlátozások) figyelembevételével, számítógépes matematikai módszerekkel.

Így a kiinduló szerkezeti megoldásnál jobb megoldások határozhatók meg, amelyek tömeg- és költségcsökkenést eredményezhetnek a tervezési stádiumban.

Az elmúlt évtizedek egyik legfontosabb mőszaki tevékenysége az úgynevezett Tartószerkezeti Eurocode-ok kidolgozása volt. E szabványsorozat elıkészítése, összeállítása és a bennük foglalt elıírások megismertetése rendkívül nagy feladat, hiszen igen különbözı mérnöki módszereket, eljárásokat és szokásokat kell harmonizálni.

Jelen könyv azt tőzi ki célul, hogy acélszerkezetek tőzteherre történı méretezésével foglalkozzon, a dolog természetébıl adódóan teljes körő ismertetést nem vállal, hanem arra törekszik, hogy az alapelveket megismertesse, a részletek vonatkozásában eligazítást adjon és egyszerő számpélda segítségével bemutassa a követendı eljárásokat. A könyv feldolgozza a tőzteherrel és hatásával foglalkozó fontosabb szabványokat.

Ahhoz, hogy a tőzteher és hatásait vizsgáló eljárások jól érthetıek, beilleszthetıek legyenek a tervezési folyamatba, megismételjük az Eurocode szabványcsalád azon részeit, melyek a teljes körő áttekintés megszerzéséhez szükségesnek adódnak, így a könyv áttekinti a szabványcsalád általános részeit.

A mérnöki szerkezeteknek biztonságosaknak, gyárthatóaknak és gazdaságosaknak kell lenniük. Az optimális méretezési rendszerben a biztonságot és gyárthatóságot a méretezési és gyártási feltételek teljesítésével lehet szavatolni, a gazdaságosságot a költségfüggvény minimálásával lehet elérni. Ehhez a rendszerhez ki kellett dolgozni a költségelemzést fıleg hegesztett szerkezetekre és alkalmazni kellett a korlátos függvény-minimálás modern matematikai módszereit.

Az itt szereplı fejezetek összefoglalják a matematikai módszereket, a költségszámítást valamint az Eurocodok tőzbiztos szerkezetek tervezésére vonatkozó elıírásait.

Kidolgozásra került több keret optimális méretezése tőzbiztonságra, illetve a tőzvédı bevonat alkalmazási lehetısége lett bemutatva.

A könyv a reális modelleken bemutatott szempontokkal segítheti a tervezıket, kutatókat, gyártókat és hallgatókat jobb, optimális, versenyképes szerkezet-megoldások kifejlesztésében.

A könyvet hasznosan forgathatják a gyakorló szakemberek, mérnökök, sıt a döntéshozatal többféle szintjén álló vezetık is.

Köszönetet mondunk a TÁMOP-4.1.2-08/1/A-2009-0001 „Korszerő anyag-, nano- és gépészeti technológiákhoz kapcsolódó mőszaki képzési területeken kompetencia alapú, komplex digitális tananyag modulok létrehozása és on-line hozzáférésük megvalósítása”

program támogatásáért. Valamint köszönet családjainknak a mindennapi közvetlen és közvetett és szavakban sokszor ki nem fejezhetı segítségért.

A szerzık

1 Az optimális méretezés újabb módszerei

1.1 Bevezetés

A szerkezetoptimálás során a mérnöknek jól kell ismernie a szerkezet viselkedését, a feszültségeket, alakváltozásokat, a stabilitási viselkedést, a sajátfrekvenciát, a rezgéscsillapítást, stb. Másik fontos elem a megbízható optimáló módszer alkalmazása az optimum megtalálása során. A kérdés mindig ugyanaz: melyik a legjobb, a legmegbízhatóbb eljárás? A válasz az, hogy az a legjobb módszer, amelyiket a felhasználó a legjobban ismer.

Egyik algoritmus sem tökéletes. Mindegyiknek van elınye és hátránya is.

Szerkezetoptimálással kapcsolatos munkánk során számos algoritmust alkalmaztunk az évtizedek alatt. Ezek ismertetésre is kerültek könyveinkben és számos mérnöki alkalmazáson keresztül (Farkas 1984, Farkas & Jármai 1997, 2003, 2008). A legtöbb eljárást módosítani kellett, hogy mérnöki alkalmazásra hatékony legyen.

Nagyszámú egycélfüggvényes optimáló algoritmus létezik, amint azt ismertettük is Farkas &

Jármai (1997) könyvben. A deriváltat nem igénylı módszerek a következık: Komplex (Box 1965), Rugalmas Tolerancia (Himmelblau 1971) és Hillclimb (Rosenbrock 1960). Elsı deriváltat igénylı módszerek: Sequential Unconstrained Minimization Technique (SUMT) (Fiacco & McCormick 1968), Davidon-Fletcher-Powell (Rao 1984), etc. Második deriváltat igénylı módszerek: Newton (Mordecai 2003), Sequential Quadratic Programming, SQP (Fan et al. 1988), a Feasible SQP (Zhou & Tits 1996). Vannak az optimáló módszereknek más osztályai is, mint például az Optimalitási Kritérium módszer (OC) (Rozvany 1997), vagy olyan diszkrét módszer, mint a Backtrack (Golomb & Baumert (1965), Annamalai 1970), az entrópia-alapú módszerek (Simões & Negrão 2000) (Farkas et al. 2005), stb.

A többcélfüggvényes optimáló módszerek akkor fontosak, amikor többcélfüggvény együttes figyelembevétele mellett kompromisszumos megoldást keresünk (Osyczka 1984, 1992, Koski 1994).

Az egycélfüggvényes optimálás matematikai megfogalmazása a következı:

minimálja a függvényt f(x) x₁,x₂,...,x_N , (1.1)

a következı feltételek mellett g_j(x)≤0, j=1,2,...,P, (1.2)

h_i(x)=0 i=P+1,...,P+M , (1.3)

ahol f(x) egy többváltozós nemlineáris függvény, gj(x) és hi(x) nemlineáris egyenlıtlenségi és egyenlıségi feltételek.

Az elmúlt két évtizedben új eljárások jelentek meg, mint például az evolúciós módszerek, a Genetikus Algoritmus (GA) Goldberg (1989), a Differenciális Evolúció (DE) Storn & Price (1995), a Hangyaboly módszer (Ant colony) (Dorigo et al. 1999), a Részecskecsoport Optimáló módszere (Particle Swrm Optimization, PSO) Kennedy & Eberhart (1995), Millonas (1994) és a Mesterséges Immune Rendszer (Artificial Immune System AIS) (Farmer et al. (1986), de Castro & Timmis (2001), Dasgupta (1999). Más, szintén hatékony módszerek, mint a Leap-frog a potenciális energia minimuma analógiájára (Snyman 1983, 2005), a VEM eljáráshoz hasonlóan kerültek kifejlesztésre.

1.2 Genetikus algoritmus

1.2.1 A genetikus algoritmus alapelve

A genetikus algoritmus (GA) egy olyan problémafüggetlen metaheurisztika, amely általános keresési terekben végez optimálást. Megoldás populációk sorozatát állítja elı különbözı operátorok segítségével, amelyek közül a legfontosabbak a rátermett szülık kiválasztását végzı szelekció, és a szülıkbıl új megoldásokat elıállító keresztezés és mutáció. A genetikus algoritmus alkalmazásához szükség van keresési teret adó megoldások kódolására, ahol a kód analóg az örökítıanyaggal. E módszernél egy populáció egyedei, ezek jelképezik a különféle potenciális megoldásokat, küzdenek a túlélésért. A túlélést egy egyed számára a feladat megoldásában való eredményessége biztosítja.

Az egyedek génekkel rendelkeznek, ezekbıl épülnek fel. A gének írják le külsı-belsı állapotukat, „milyenségüket”: ezek a feladatrendszer leképzésének alapelemei (változók, ismeretlenek stb.). Az egyedek öröklıdési folyamata során az utódok e géneket viszik tovább.

A módszerben elıször is a feladatban szereplı ismeretleneket képezzük le génekké, a géneket pedig kromoszómákká, melyekkel az egyedeket építjük fel. Ezután különbözı szabályok alapján két véletlenszerően kiválasztott egyedet különféle génmanipuláló mőveleteknek vetünk alá, aminek az eredménye hasonló, vagy épp eltérı génekkel rendelkezı egyedek megjelenése lesz. Az utód egyedek egyes génszakaszaikban szüleik szekvenciáit öröklik, míg másokat mutációval kaphatnak. A mutáció valószínőségét viszonylag alacsony szinten célszerő tartani.

Az egyedek mindegyike rendelkezik egy mutatóval, amellyel eredményességét mérjük.

Például: egy tömeg-, vagy költségoptimum számító programnál a tömeg, vagy költség lehet

ez a szám. Minél kisebb a tömeg, vagy a költség, annál jobb az adott megoldás – azaz fordított arányosságról beszélünk a hibaérték és az eredményesség tekintetében.

E jellemzı alapján lehet sorrendet felállítani az egyedek között és a kevésbé eredményes egyedeket eltávolítjuk, míg a többi egyed a populációban marad, miáltal is a hibaérték állandóan közelíteni fog az ideális minimumhoz. Egy jó (vagy jobb) eredmény még jobb eredményeket szül és így egyre kisebb részterület körül fog szóródni a kimenet, a szóródás mértéke egyre csökken – az egészen (vagy a részben) optimális megoldásig (de Jong 1975, Chan 1998).

1.2.2 A genetikus algoritmus operátorai

Szelekció

A populációból véletlenszerően kerülnek kiválasztásra azon egyedek, melyek, mint szülık játszanak szerepet a következı generáció kialakulásában. Általában az eredményességi mutató „fitness” szolgál a kiválasztás alapjául (Goldberg 1989). Az eredményesebb egyedeknek nagyobb esélyük van arra, hogy bekerüljenek a következı generációba (a rulettkeréken nagyobb rész jut nekik, ami arányos az eredményességgel).

Egy másik szelekciós forma a versenyeztetés, ahol az egyedek egy csoportja véletlenszerően kerül kiválasztásra. A csoportból a legjobb lesz szülınek választva. A folyamat folytatódik, hogy a párja is kiválasztásra kerüljön. Whitley (1989) szerint két gyenge pontja van annak, ha a kiválasztás az egyed „jóságán” alapul: a stagnálás és a túl korai konvergencia. Mindkét probléma abból ered, hogy a legjobb egyedek dominálnak a következı generációban. A versenyeztetés esetén minden egyednek egyenlı az esélye a kiválasztásra, ezért ez a módszer mentes az elıbb említett problémáktól.

Keresztezés

A keresztezés teszi lehetıvé. hogy a tervezési jellemzıket változassuk, függıen a keresztezés valószínőségétıl, hogy jobb tervezési megoldásokat állítsunk elı. A keresztezés során a szülık kromoszómáinak egyes szakaszait párosítjuk és ezzel képezzünk egy új egyedet.

Az egypontos keresztezés a legegyszerőbb, de vannak hátrányai. Ezzel a módszerrel a kromoszóma két szakaszának párosítása történik, ami korlátozza a lehetıségeket. Néha csak egy rövid szakaszát kell a kromoszómának cserélni, de ez a módszer a teljes szakaszt cseréli a keresztezési pont után, ami pozicionális eltolódást okoz. Ez azt jelenti, hogy hosszú kromoszómaláncot tönkretesz egy egypontos keresztezés. A szegmensek cseréje a szülık között mindig magában foglalja a végek cseréjét is, amit végpont-hatásnak neveznek.

Továbbá olyan keresztezés, melynél a keresztezési pont után egyformák a kromoszómák, nincs értelme, mert akkor a gyerek ugyanolyan, mint a szülı. Ezen problémákat a kétpontos keresztezéssel kerülhetjük ki általában.

Váltakozó irányú keresztezés

Ez tulajdonképpen nem egy különálló operátor, hanem hasonlóan a mutációhoz, ezt is a hagyományos keresztezési eljárásba építve alkalmazzuk. Mivel a keresztezés során a

kromoszóma elsı harmada kisebb mértékben (gyakran egyáltalán nem) vesz részt a populáció fejlıdését elısegítı bitcserében, ezért szükséges bevezetni ezt az operátort. Lényege az, hogy a keresztezést ötven-ötven százalékos valószínőséggel a keresztezési hely elıtt illetve a keresztezési hely után végezzük el, melynek köszönhetıen a kromoszóma teljes hosszán létrejöhet az optimálás szempontjából elınyös cserélıdés.

Mutáció

A mutáció a kromoszómát alkotó egyik változó véletlenszerő változtatása. A mutációs operátor változtatja a karakter értékét 0 és 1 között a mutáció valószínőségének megfelelıen.

A mutáció egy védı tényezı a túl korai konvergencia elkerüléséhez (Goldberg 1989).

Kiválasztottak stratégiája (elit)

Kiválasztottak stratégiáját (klónozás) de Jong vezette be, mellyel a legjobb tulajdonságokat mutató egyedeket a populációban átviszi a következı generációba. Ezáltal a legjobb egyedek nem vesznek el keresztezés, vagy mutáció által és a jóság függvény maximuma növekszik a következı generációban. Az optimális hatáshoz az egyedek kb. 1-2 százalékát használja fel így.

Laboratórium operátor

Másik lehetıség, hogy elkerüljük a stagnálás és a korai konvergencia problémáját, amit a domináló egyedek okoznak, az a Whitley (1989) által javasolt módszer, amikor az adott populációban domináló egyedet betesszük az un. „laboratóriumba”. Az eljáráshoz a felhasznált diszkrét értékeket változónként növekvı vagy csökkenı sorrendbe rendezzük.

Mindegyik diszkrét értéket a legkisebbtıl a legnagyobbig egy helyiértékkel látunk el, annak megfelelıen, hogy sorrendben hányadik helyet foglalja el az egy változóhoz tartozó értékek (itt pl. szelvényméretek) sorában. Az adott populációban megkeressük azt az egyedet, amelyikhez a legkisebb célfüggvényérték tartozik. Ezen az egyeden vizsgálatokat végzünk oly módon, hogy az egyedhez tartozó változók értékét egy, kettı, ill. három helyiértékkel megváltoztatjuk. A helyiérték megváltoztatásának mértékét ill. a helyiérték megváltoztatásának elıjelét véletlenszerőségi elven határozzuk meg.

Populációnként több száz ilyen kísérleti egyedet hozhatunk létre és megvizsgáljuk, hogy az egyes egyedekhez tartozó célfüggvényérték kisebb-e az addigi legjobbnak vélt egyed célfüggvény értékénél? Ha kisebb, akkor az egyedet a soron következı populációba klónozzuk.

Méretezési feltételek kezelése

A visszautasító stratégia (rejecting strategy) és a büntetıfüggvények módszere (penalty approach) a két fı módszer a méretezési feltételek kezelésére. A büntetıfüggvények módszerénél a feltételes optimálást feltételnélküli optimálássá konvertáljuk azáltal, hogy a célfüggvényhez hozzáadjuk az összes megsértett feltételt a következı módon:

{ }







 +

+

=

∑ ∑

= =

M

j

l

k k j

k

k ) f(x) r max[ ,g (x)] [h (x)]

r , x ( F

1 1

2 2

0 (1.4)

ahol r_k a büntetı paraméter, a határ lim_→∞Fmin = fmin

rk .

A büntetıfüggvény elsı része jelenti a pozitív részt, ami a maximum értéke a (0, g_j(x)) tartományon.

A GA megoldás pontossága a valódi optimumtól jelentısen függ a büntetı paraméter értékétıl. Ha a büntetı paraméter közepes értékő, a módszer egy nem-megfelelı pontba konvergál. Másrészrıl ha a büntetı paraméter értéke túl nagy, akkor a módszer a visszautasító stratégiával lesz egyenlı. Számos módszert javasoltak a büntetıfüggvényes területen (Michalewicz 1995). A kvadratikus büntetı függvény az egyike a kutatók által használt legáltalánosabb büntetıfüggvényeknek. Megfigyelték, hogy ha a méretezési feltételek normáltak, akkor az egynél kisebb kitevı alkalmazása felnagyíthatja a feltételek kismértékő megsértését, jobban, mint a tradicionális kvadratikus alak.

Kódolás

Az alap GA algoritmusnál a bináris kódolást alkalmazták (Goldberg 1989). A tradicionális bináris kódolásnál egy gyenge tulajdonsága ismert, a valódi paraméter nagy változása egy bit csere esetén, mint például a két bináris szám 0111111 és 1111111, melyek egyenlıek 63-al és 127-el. Az eltérés nagy miközben csak egy bináris elem változott.

Az un. szürke kódolás egy másik út a paraméterek binárissá alakításánál, aminek az a tulajdonsága, hogy egy lépéssel változtatva a tervezési változók értékét az egy bites változást eredményez a bináris értéknél.

Számos könyv, cikk és konferencia elıadás található ebben a témában. A Genetikus Algoritmus népszerősége még ma is nagy amiatt, hogy nem-konvex optimálási feladatoknál is jól alkalmazható.

1.2.3 A használt genetikus algoritmus optimumkeresési folyamatának lépései

a) Az elsı populáció létrehozása (indításkor);

b) Az populáció jellemzıinek (jósági értékek, a legjobb egyed kiválasztása stb.) meghatározása;

c) A szülık kiválasztása;

d) Keresztezés, váltakozó irányú keresztezés és a mutáció elvégzése;

e) Laboratóriumi operátor (+ klónozás);

f) Klónozás;

g) Az új populáció létrehozása (ismétlés a b) ponttól);

1.3 Differenciális evolúció

Price & Storn mutatta be az 1990-es években a Differenciális Evolúció módszerét (DE) (Storn

& Price 1995, Storn 1996). Ez a módszer eredetileg folytonos változókra készült, de a továbbfejlesztett verziója képes diszkrét, illetve kevert változókat is kezelni. Elsı látásra a DE módszer elınye, hogy nincs szükség komplikált kódolásra, mint a GA-nál.

A DE magjának egy nagyon egyszerő leírása a következı:

(1) Válasszon egy célvektort,

(2) válasszon ki véletlenszerően két vektort a populációból,

(3) alakítson ki egy súlyozott különbségvektort ebbıl a két vektorból,

(4) adjon hozzá egy véletlenül kiválasztott harmadik vektort a különbséghez, (5) végezzen keresztezést a célvektornál, hogy megkapja a vizsgált vektort,

(6) ha a vizsgált vektorhoz kisebb érték tartozik, mint a célvektorhoz, akkor átmehet a következı generációba, egyébként menjen ismét a 2-es lépéshez.

A populáció egyedei a valódi alakjukban szerepelnek, így a számítás idıigénye kisebb, de ez nem jelenti azt, hogy a DE hamarabb tudja megtalálni az optimumot. Ez sok tényezıtıl függ.

Elıször nézzük meg, hogyan végzi a számítást diszkrét értékek esetén.

Általában az optimálandó függvény f a következı alakú:

f(y_i ) i=1,...,N (1.5)

ahol

a) y_i = x_i folytonos értékek esetén, b) yi = DISC(xi

c) ) diszkrét értékek esetén.

DISC() egy függvény, mely konvertálja a x_i valódi értékét a legközelebbi diszkrét értékbe. A járatos diszkrét értékek elıre megadásra kerülnek. N a tervezési változók száma.

Azért, hogy az optimum keresés kezdıpontját létrehozzuk szükséges a populáció létrehozása.

A kezdeti populáció, PG=0, véletlen számok felhasználásával a peremfeltételek alapján.

^{P0 = xi,j,0 =randj}

[ ]

(

)

A DE önhivatkozó reprodukciós sémája különbözı minden más evolúciós algoritmustól. Az elsı generációtól végig, az adott populáció vektora PG, illetve annak egyedei véletlenszerően kombinálásra kerülnek, hogy képezzék a következı populációt P_G+1. A jelöltek csoportja, a

‘próbavektor’ P’_G+1=U_i,G+1=u_i,j,G+1 a következı módon kerül kiválasztásra:

Ha ^randj

[ ]

^vi,j,G₊1 =^xr3,j,G +^F(xr1,j,G −^xr2,j,G ⁾

egyébként ui,j,G+1 = xi,j,G . ahol i = 1,…,NP, j = 1,…,N

^k∈

{

}

{

}

^CR∈

{

}

{

}

figyelembe véve, hogy

Ha ui,j,G₊₁<xj^(L), akkor u_i,j,G+1=DISC(x_j^(L)), vagy

ha u_i,j,G+1>x_j^(U), akkor u_i,j,G+1 =DISC(x_j^(U)), egyébként ui,j,G+1 = ui,j,G. (1.8)

F és CR az eljárás ellenırzı paraméterei. Hasonlóan NP-hez, mindkét érték változatlan a keresési folyamat során. F felsı határát tapasztalati úton határozhatjuk meg. CR egy valós értékő keresztezési tényezı, ami a kísérleti vektor paraméterét szabályozza, ami véletlen módon választható a változtatott vektorból vi,j,G+1 a jelenlegi vektor xi,j,G helyett.

Általánosságban mind F és CR értékei a konvergencia gyorsaságára és az eljárás robosztusságára vannak hatással.

A következı populáció P_G+1 tagjai a jelenlegi populációból P_G kerülnek kiválasztásra, és a gyermekpopuláció a következı szabály szerint kerül kiválasztásra:

Ha f(u_i,G+1)≤ f(X_i,G), akkor X_i,G+1 = u_i,G+1 (1.9)

egyébként X_i,G+1 = X_i,G .

A feltételek kezelése a legtöbb DE verzióban büntetıfüggvénnyel történik. Van módszer, ahol nincs büntetıfüggvény. Ekkor az alpopulációban vagy a méretezési feltétel értéke, vagy a megsértett feltételek száma a célfüggvény, amit minimál a program.

Lampinen bevezetett egy hibrid módszert a feltételek kezelésére. Ez összehasonlítja az adott populáció elemét a neki megfelelı vizsgálati vektor (a lehetséges új populáció) megfelelı elemével. A vizsgálati vektor akkor kerül kiválasztásra, ha az alábbi három feltétel teljesül:

(1) minden feltételt kielégít és kisebb, vagy egyenlı függvényértéket ad. Ebben az esetben mindkét összehasonlított verzió megfelelı,

(2) a vizsgálati verzió megfelelı, miközben a neki megfelelı jelenlegi populációban lévı tag nem megfelelı,

(3) a vizsgálati pont nem megfelelı, de kisebb, vagy egyenlı értéket ad az összes feltételre.

Abban az esetben, ha nem megfelelı a megoldás, akkor a program nem hasonlítja össze a célfüggvény értékeket. Ekkor egy hatékony kiválasztás történik, hogy megtalálja az elsı megfelelı megoldást. Az eredmény egy gyors konvergencia a megengedett tartomány irányába.

Ha a vizsgált vektor eleme ugyanolyan jónak tekinthetı, mint a jelenlegi populáció megfelelı eleme, akkor mehet be a következı populációba. Ez a feltétel segít abban, hogy elkerüljük a stagnálást.

A leállító kritérium a DE-nél függ a probléma jellegétıl. A tervezési folyamat megállítható, ha egy is a populációból teljesíti a feltételeket, vagyis megtalálja a paraméter értékeket a megengedett tartományon. Szélsıértéket keresve a határ, ami megállítja az eljárást, általában a generációk száma.

Összességében csak négy paraméter vezérli az evolúciót: a populáció mérete NP, a súlyozás w, amit a különbözeti változásnál használ, a CR állandó, mely a keresztezést irányítja és a generációszám.

A DE-t számos különbözı szerkezetoptimálási problémára alkalmazták, mint alakoptimálás, keret tervezés, rácsos tartó optimálás, stb.

Nagyszámú könyv, cikk és konferencia anyag, mely a Differenciális Evolúcióval foglalkozik megtalálható az interneten, sıt még programok is.

Differential Evolution Homepage

http://www.icsi.berkeley.edu/~storn/code.html

1.4 A Snyman-Fatti módszer

Az itt ismertetett globális módszer a Snyman-Fatti (SF) algoritmus, mely több kezdıpontú globális minimáló algoritmus dinamikus keresési irányokkal globális folytonos feltétel nélküli optimálásra (Snyman & Fatti 1987, Groenwold & Snyman 2002). A módszer nemrég átdolgozásra került (Snyman & Kok 2007), hogy növeljék a hatékonyságát és hogy feltételes optimálásra alkalmazható legyen. Az eredményként adódó számítógépi program alkalmazhatóságát és hatékonyságát más, jelenleg leginkább hatékonynak tartott evolúciós globális optimáló módszerekkel hasonlítottuk össze standard tesztproblémákon. A részletesebb elméleti leíráshoz és bemutatáshoz az olvasónak a módszer eredeti leírását javasoljuk (Snyman & Fatti 1987). Itt egy összefoglaló jellegő leírást adunk.

Tekintsük az eredeti feltételes egyenlıtlenségi problémát:

( ) [

]

t r w

R x

x x

f , = , ,… ∈

minimáljuk _{1 2}

. . .

x x

x

,

(1.10)

egyenlıtlenségi feltételek esetén:

^gj

( )

A feladat optimális megoldását x*-al jelöljük, melyhez tartozó optimális célfüggvény értéke f(x*).

Az (1.10) egyenletben megadott feltételes optimálási feladatot feltétel nélkülivé alakítjuk büntetıfüggvény bevezetésével. Az F(x) függvény optimumát keressük az SF módszerrel. Az F(x) büntetıfüggvény a következı módon van definiálva:

²

1

} ) ( { )

( )

(

∑

=

+

= ^m

j j g f

F x x ρ x ,

(1.11)

Ahol ρj = 0 ha gj(x) ≤0, egyébként ρj = µ (egy nagy szám).

Mivel feltétel nélküli globális optimálási problémánk van, kijelenthetjük: a folytonosan differenciálható F(x) célfüggvényhez: keressük meg az x*(µ) úgy, hogy a változó a megadott tartományon mozog, X⊂Rⁿ

F* = F(x*(µ) = minimuma az F(x) függvénynél a tartományon x ∈X.

(1.12)

Az SF algoritmus, ami alapvetıen egy több kezdıpontú eljárás, számos pontból elindul a vizsgált tartományon X (általában egy négyszög tartomány Rⁿ), és a lokális keresést végrehajtjuk minden minta pontnál. A módszer heurisztikus olyan szempontból, hogy a legkisebb minimumot találja meg véges számú keresés után mint egy becslése F*-nak.

A helyi keresés során az SF algoritmus végigvizsgálja a változók terét X-et, úgy hogy a keresési irányokat meghatározza a következı differenciál egyenletbıl:

ɺ x ɺ = - ∇ F(x(t))

(1.13)

ahol ∇F az F(x) célfüggvény gradiens vektora.

Az (1.13) egyenlet megadja az egységnyi tömeg mozgását az n-dimenziós konzervatív erıtérben, ahol F(x(t)) reprezentálja a tömeg potenciális energiáját x(t) pozícióban. Az itt generált keresési irányok hasonlóak a Snyman-féle dinamikus módszernél helyi optimálás esetén (Snyman 1982, 1983). Az SF globális módszernél az irányok meghatározása módosításra került oly módon, hogy számos lokális minimum esetén is nagy valószínőséggel biztosítja a konvergenciát a legkisebb lokális minimumhoz, melyet a konvencionális gradiens lokális keresı módszerek elértek volna el.

A speciális módosítások megnövelték a konvergencia tartományt a legkisebb minimumnál, különösen a globális minimumnál. A konvergencia kritériumot a Bayesian valószínőségi értékbıl határozza meg eldöntve, mikor fejezi be a globális mintavételt és fogadja el a minimum értéket F-nél, mint globális minimum F*-ot.

Kezdeti feltételként a helyzetre x(0) = x⁰ a sebességre xɺ(0) = v(0) = v⁰ = 0, integrálva (1.13)- et a 0-tól t-ig, megkapjuk az energia megmaradási összefüggést:

¹₂

v ( t )

+ F( x (t)) =

v (0)

+ F( x (0)) = F( x (0))

(1.14)

az (1.14) egyenlet baloldalának elsı része jelenti az egységnyi tömeg kinetikus energiáját, a második része pedig a helyzeti energiáját egy adott t idıben. Nyilvánvalóan a tömeg elkezd mozogni a legmeredekebb esés irányában és a kinetikus energiája növekedni fog, miközben F értéke csökken mindaddig, amíg lefelé mozog, vagyis -∇F·v>0.

Ha nincs tovább süllyedés a generált útvonalon, akkor a v sebesség nagysága csökkenni kezd és felfelé kezd mozogni a test és változik a lokális minimum iránya. Ha valószínőleg több, vagy legalább egy lokális minimálás történt, akkor kíváncsiak vagyunk a globális minimumra.

Egy reális globális stratégia figyelni az irányokat és rögzíteni az x^m pontot, a hozzá tartozó sebességet v^m =xɺ^m és a célfüggvény értékét F^m, ahol a minimum a vizsgálat során elıfordult.

Hagyjuk a testet tovább mozogni háborítatlanul a tárolt energiájával. Ezt abban a reményben tesszük, hogy elér egy hegyhátot F^r, F^m < F^r < F(x(0) és folytatva útját egy még kisebb célfüggvényt talál.

Másrészrıl szükséges a mozgási pályát befejezni mielıtt visszafutás következne be, vagy hozzávetılegesen visszafuttatná magát egy nem definiált periodikus, vagy ergodikus (tér- kitöltı) mozgással. A megfelelı leállítási feltétel az SF algoritmusnál, hogy befejezzük az elsı mozgási pályát, amikor elér egy olyan függvényértéket, ami közeli az induló értékhez F^s

= F(x(0)) miközben még felfelé halad, vagyis ∇F·v > 0. Ennél a pontnál, amikor a megállítás megtörténik, a legjobb pontot rögzítjük x^b := x^m , mely a célfüggvény következı értékéhez tartozik F^b: = F^m. Elindítunk egy segéd-keresést, vagy belsı mozgást egy új belsı kezdıpontból x^s: = ½(x⁰+x^b) melynél a kezdısebesség ½ v^m és a célfüggvény kezdı értéke F^s

= F(x^s). Ennél az új segéd, vagy belsı mozgásnál a függvényértéket szintén figyeljük és x^m és a hozzá kapcsolódó v^m értékeit rögzítjük.

Ennek a megállításakor, amikor a célfüggvény értéke eléri, vagy megközelíti F^s értékét, miközben felfelé mozog, a kezdıpontot a következı mozgáshoz választjuk, mint x^s = ½(x^s +x^b) a kezdeti sebességgel ½v^m, ahol x^b ismét a legjobb pont az adott szakaszon. A belsı mozgásirányok ezen generálása egymást követı sorozatban történik, amíg x^b konvergál, vagy

) (x^b

∇F gyakorlatilag zérus.

Természetesen a fenti stratégia feltételezi, hogy a mozgásirány az (1.13) differenciál-egyenlet megoldásából adódik és pontosan ismert minden idıben. A valóságban ez nem lehetséges és a mozgásirányok generálása numerikusan történik a bakugrás elve szerint (Snyman 1982):

Adott egy kezdıpont x⁰ = x(0), egy kezdeti sebesség v⁰ = v(0) = x^ɺ(0) és egy idılépés ∆t, számítsuk ki k = 0,1,2,…-ra

x^k+1=x^k+v^k∆t, (1.15)

v^k+1=v^k-∇^F(xk+1)∆t . (1.16)

Az elsı lépésnél v⁰:= ½∇F(x⁰)∆t. Tapasztalati módszer alapján becsüljük az idılépést ∆t (Snyman, Kok 2007). Ha a belsı, illetve segéd mozgások során egy adott iterációnál megáll a módszer egy lokális minimumban x^k+1, ahol a célfüggvény értéke F^k+1, a program megvizsgálja, mennyi a valószínősége, hogy a lokális minimum egyben globális minimum is.

Az algoritmus ezen globális komponense egy sztochasztikus feltételt jelent, mely a legkisebb elért minimum valószínőségét vizsgálja, hogy nem globális-e (Snyman, Fatti 1987).

Ha megtaláltuk a globális minimumot x*(µ), akkor az (1.9) képletnek megfelelı büntetıfüggvény segítségével meghatározzuk az aktív feltételeket. A pontos megoldást x*-ot a feltételes problémára úgy kapjuk meg, hogy egyidıben a mozgatásos módszert használjuk ás minimáljuk az aktív feltételek megsértésének négyzetösszegét a x*(µ) kezdıpont felhasználásával.

Az SF algoritmust sikeresen alkalmazták számos szerkezetoptimálási probléma megoldásánál, mint pl. bordázott lemezeknél Farkas et al. (2007a), Snyman, Kok (2007).

1.5 A Részecskecsoport módszer

Azon programok, melyek konvex függvények optimálására jók, sokszor gyengén szerepelnek, amikor egy függvénynek sok lokális minimuma, vagy maximuma van. Sokszor megakadnak egy lokális minimumnál/maximumnál. Számos módszert fejlesztettek arra, hogy el tudja kerülni ezen lokális optimumokat. A Részecskecsoport Módszer egy ilyen globális optimálási módszer.

A Részecskecsoport Módszer (PSO) az evolúciós módszerek egy viszonylag új osztálya, mely alkalmas lehet az optimális megoldás x* megkeresésére általános optimálási feladatnál. Az eredeti PSO algoritmus, melyet Kennedy és Eberhardt (1995) javasolt, a nagy csoportokban élı élılények szociális viselkedésén, egymásra-hatásán alapszik. A PSO különösen csapatviselkedéseket szimulál, amelyek legjobban madárcsapat, halraj, méhraj esetén érzékelhetıek. A PSO algoritmust könnyő adaptálni a különbözı programnyelveken, mivel a magja csak néhány soros. Bebizonyosodott az alkalmazások során, hogy egyszerre gyors és hatékony, fıként erısen nemlineáris optimálási problémánál kerül alkalmazásra. A PSO módszer különösen hasznos paraméteres optimálásra folytonos, többdimenziós térben.

Ahhoz, hogy végrehajtsunk egy optimálást a többdimenziós térben, a PSO irány vektorokat és sebességeket ad meg minden elemnek (részecskének) a csoportban az ı konkrét pozíciójában.

Minden részecske ezután “mozog”, vagy „repül” a vizsgálati térben a részecske megadott sebességével, melyet módosíthat irányában és nagyságában a többi részecske a környezetében. Ezek a helyi hatások a szomszédos részecskéknél terjednek aztán végig a teljes csoporton és ezáltal kerül a csoport kedvezıbb helyzetbe, közelebb a probléma (1.4) megoldásához. A határok, melyeken belül a részecskék hatni tudnak a többire az a “fitness”, a megfelelés mértéke, mely azt mutatja, hogy az adott részecske mennyire jó, a többi részecske

“jóságához” képest. Az evolúciós elv “survival of the fittest” (természetes kiválasztódás)

játszik szerepet csakúgy, mint a részecskék szociális viselkedése a “kövesd a helyi vezetıt”

hatása, a kiemelkedı minta hatása.

Továbbá az egyes egyedek tanulnak másoktól, különösen a legjobbtól közülük. Az emberek is tanulnak saját tapasztalataikból és a sikeres szomszédaiktól. A Részecskecsoport Módszer ezt a viselkedést utánozza. Minden egyed a csoportban egy elem a többdimenziós térben a pozíciójával és a sebességével. Ezen egyedek repülnek a hipertérben és emlékeznek a korábbi legjobb pozíciójukra. A rajban lévı egyedek kommunikálnak egymással és igazítják a pozíciójukat és sebességüket a jobb pozíciókhoz.

A Részecskecsoport Módszer a korlátozott ésszerőség és a decentralizált döntéshozatal elvén alapul a globális optimum keresésekor. Sikerrel alkalmazták nagyon nehéz, sok lokális optimummal bíró probléma esetén is.

A módszer nem igényel deriváltakat és képes a célfüggvény globális optimumát meghatározni. A méretezési feltételek a büntetıfüggvények módszerével kezelhetık.

Újabban a PSO-t sikeresen alkalmazták alakoptimálásra és szerkezetoptimálásra (Fourie &

Groenwold 2000). Egy operátor, az ’ırült madár’ újra bevezetésre került a dinamikusan változó maximális sebességek és inercia bevezetése mellett.

Az eljárás pszeudó kódja a következı: I) Minden egyes egyedre:

Azonosítja az egyedeket II) Do:

a) Minden egyes egyedre:

1) Kiszámolja a jósági értéket (fitness value)

2) Ha a jósági érték jobb, mint a korábbi legjobb érték (pbest), 3) Akkor a pbest értékét módosítja

Vége

b) Minden egyes egyedre:

1) Megkeresi az egyed környezetét és abban a legjobb jósági értékő egyedet 2) Kiszámolja az egyed sebességét a képletbıl (1.15)

3) Alkalmazza a sebesség korlátozást

4) Meghatározza az egyed új pozícióját (1.16) 5) Alkalmazza a pozíció korlátozást

Vége

While miközben a maximum iterációszám, vagy a konvergencia kritérium nem teljesül.

Egy jóval részletesebb leírása a PSO algoritmusnak, ahol büntetıfüggvényt alkalmaztunk a feltételek kezelésére, a következı:

1.6 Az alap PSO algoritmus

1) Adott M, kmax, Nmax. Beállítja az idıpillanatot k = 0, ^F_i^{b = Fg =F}before^g =^∞. Létrehoz egy véletlenszerő csoportot (csapatot) az M részecskére (csoporttagok), megadva a

véletlenszerő kezdeti pozíciójukat x ⁰ⁱ (megoldásjelölt) csakúgy, mint a véletlenszerő kezdeti sebességüket vi⁰, minden részecskénél i, i=1,2,…,M. Ezután minden részecskére a pályagörbe számítása történik a következı módon,

2) Adott k idıpillanatban kiszámítja minden egyes részecske i “jóságát” egy konkrét pontban

k

xi azáltal, hogy meghatározza _{F x( i}^k₎ értékét. A minimálás (1) szerint úgy valósul meg, hogy melyik részecskénél kisebb a célfüggvény F x( _i^k) értéke, hol nagyobb a részecske

„jósága”.

3) Minden i=1,2,…,M:

ha F( x_i^k)≤F_i^b akkor legyen F_i^b=F(x_i^k) és p_i^b=x_i^k {a legjobb pont az i pályagörbén}

ha k b i^k

i g g

k

i ) F F F )

F(x ≤ akkor legyen = (x ésg = x {legjobb globális pont}

4) Ha F^g<F_before^g akkor legyen N=1, egyébként legyen N=N+1.

5) Ha N> N_max vagy k> k_max akkor STOP és legyen x* = g^b; egyébként folytassa.

6) Új sebességek és részecske pozíciók meghatározása k+1-re a szabályok alkalmazásával:

Minden i=1,2,…,M:

v^k_i⁺¹:=v_i^k +c₁r₁(p_i^b−x_i^k)+c₂r₂(g^b−x_i^k ) (1.17)

x_i^k+1:= x_i^k +v_i^k+1 (1.18)

ahol r1 és r2 egymástól függetlenül generált véletlen számok az [0,1] intervallumon, és c1, c2 megfelelıen választott paraméterek.

7) Legyen k =k+^{1 és}Fbefore^g =F^g ; menjen a 2-es pontba.

A folytonos optimálási módszert alkalmazva adaptív módon, a tervezési változók diszkrét jellegét figyelembe véve kapjuk meg a szerkezet optimális méreteit.

PSO alkalmazásra került számos szerkezetoptimálási feladatnál, mint például kétirányban bordázott merevített lemezek költségoptimálása (Farkas et al. 2007a), merevített héjak optimálása (Farkas et al. 2007b), szélturbina oszlop optimálása (Uys et al. 2007), bordázott héjak optimálása (Farkas et al. 2007c).

Az optimálás animációja látható feltétel nélkül és nemlineáris feltétel esetén az 1.1 és 1.2 ábrákon.

Irodalom

Annamalai,N.(1970) Cost optimization of welded plate girders. Dissertation, Purdue Univ. Indianapolis, Ind.

Box,M.J. (1965) A new method of constrained optimization and a comparison with other methods. Computer Journal, 8 42-52.

Dasgupta,D. (Editor), Artificial Immune Systems and Their Applications, Springer-Verlag, Inc. Berlin, January 1999, ISBN 3-540-64390-7

DeCastro,L. & Timmis,J. (2001) Artificial Immune Systems: A New Computational Intelligence Approach, ISBN 1-85233-594-7

Dorigo,M., Di Caro,G. & Gambardella, L.M. (1999) Ant algorithms for discrete optimization, Artificial Life, 5 No. 3, 137-172.

Fan,Y., Sarkar,S. & Lasdon,L. (1988) Experiments with successive quadratic programming algorithms, J. Optim.

Theory Appl. 56 pp. 359--383.

Farkas,J. & Jármai,K. (1997) Analysis and optimum design of metal structures, Balkema Publishers, Rotterdam, Brookfield, 347 p. ISBN 90 5410 669 7.

Farkas,J. & Jármai,K. (2003) Economic design of metal structures, Millpress Science Publisher, Rotterdam, 340 p. ISBN 90 77017 99 2

Farkas,J.,Jármai,K.(2008) Design and optimization of metal structures, Horwood Publishers, Chichester, UK, 328 p. ISBN: 978-1-904275-29-9

Farkas,J., Simões,M.C. & Jármai,K. (2005) Minimum cost design of a welded stiffened square plate loaded by biaxial compression, Structural and Multidisciplinary Optimization, Springer Verlag, Wien-New York, 29 No. 4, 298-303.

Farkas,J., Jármai,K. & Snyman,J.A. (2007a) Global minimum cost design of a welded square stiffened plate supported at four corners. 7^th World Congress on Structural and Multidisciplinary Optimization, WCSMO7, May 21-May.25, 2007, COEX, Seoul, Korea, Proceedings on CD, A 0381, pp. 1057-1066.

Farkas,J., Jármai,K. & Kožuh,Z. (2007b) Cost minimization of an orthogonally stiffened welded steel plate subject to static and fatigue load. Welding in the World, 51 2007, Special issue. pp. 357-366.

Farkas,J., Jármai,K. & Orbán,F. (2007c) Cost minimization of a ring-stiffened conical shell loaded by external pressure. 60^th Annual Assembly of International Institute of Welding, July 1 – July 8, 2007, Dubrovnik, Croatia, IIW-Doc. XV-1248-07, XV-F-80-07, 9 p.

Farmer,J.D., Packard N. & Perelson A., (1986) The immune system, adaptation and machine learning, Physica D, 2 187-204.

Fiacco,A.V. & McCormick,G,P. (1968) Nonlinear sequential unconstrained minimization technique. John Wiley and Sons, Inc. New York.

Fourie,P.C. & Groenwold,A.A. (2000) Particle swarm in size and shape optimisation, International Workshop on Multidisciplinary Design Optimization, 7-10, Aug. 2000, Pretoria, South Africa, Proceedings 97-106.

Goldberg,D.E. (1989) Genetic algorithms in search, optimization & machine learning, Addison-Wesley Publ.

Company, Inc.

Golomb,S.W. & Baumert,L.D. (1965) Backtrack programming, J. Assoc. Computing Machinery, 12 516-524.

Groenwold,A.A. & Snyman,J.A. (2002) Global optimization using dynamic search trajectories. J Global Optimiz; 24 51-60.

Himmelblau,D.M. (1971) Applied nonlinear programming. Mc Graw-Hill Book Co. New York.

Jármai,K. (1989a) Single- and multicriteria optimization as a tool of decision support system, Computers in Industry, Elsevier Applied Science Publishers, 11 No. 3. 249-266.

Jármai,K. (1989b) Application of decision support system on sandwich beams, verified by experiments, Computers in Industry, Elsevier Applied Science Publishers, 11 No. 3. 267-274.

Jármai,K. (2005) Particle swarm method as a new tool for structural optimization, Journal of Computational and